瞜瘯 嗦瘱 嗾喹嗉帻噍疀瘲窵璔瞡 啶喹囿唰唰啜嘧 嗳嗫璡囗啶瘱疀篫篞篞瘱喑 嘟啻嘌嘌啾瑿嘣嗷辔嗬 喙璚疀瞝瘱疀疀瑿 嘞篫瘱疀疀璚 囗啶瞡 嗒嗄嗦縌縡 [收稿日期] 2008 09 27
[作者简介] 赵天玉 (1958 ), 男, 1981 年大学毕业, 硕士, 教授, 硕士生导师, 现主要从事组合数学方面的教学与研究工作。 瞜瘯 嗦瘱 嗾喹嗉帻噍疀瘲窵璔瞡 啶喹囿唰唰啜嘧 嗳嗫璡囗啶瘱疀篫篞篞瘱喑 嘟啻嘌嘌啾瑿嘣嗷辔嗬 喙璚疀瞝瘱疀疀瑿 嘞篫瘱疀疀璚 囗啶瞡 嗒嗄嗦縌縡
与 Catalan 数 有 关 的 组 合 问 题 研 究
赵天玉, 杨 方
(长江大学信息与数学学院, 湖北 荆州 434023)
[摘要] 首先给出了 Catalan 数的 4 个经典组合模型: 凸多边形的三角剖分问题、 简单有序根树的计数问
题、 路径问题、 乘法结合方式问题, 给出了 Catalan 数的 4 种推导方法: 迭代递推方法、 生成函数方法、
组合求差方法和一一映射方法, 并综合相关文献的研究结果, 列举了 Catalan 数的一些性质。
[关键词] Catalan 数; 组合模型; 迭代递推方法; 生成函数方法; 组合求差方法; 一一映射方法
[中图分类号] O157 梃梃畅1
[MR(2000)主题分类号]05A15
[文献标识码] A [文章编号] 1673 1409 (2008) 04 N014 04
Catalan 数 C
n
是组合数学中应用广泛的重要计数函数, 它是比利时数学 E畅C畅Catalan (1814 ~1894)
在 1838 年研究组合问题时发现并提出来的
[1]
。 实际上, 大数学家 Euler 在 1758 ~1759 年研究凸多边形
的三角形剖分问题时, 就已经发现了该计数函数
[2]
, 比 Catalan 早 80 年。 随着对中国数学史的研究, 人
们发现, 中国的明安图比 Euler 早 10 ~20 年就得出该数列
[3]
, 不但应用它解决幂级数展开问题, 而且
还给出了 Catalan 数的一个几何模型
[4]
。 Catalan 数有明显的组合意义, 在唱票问题、 路径问题和不定方
程解的计数问题中有广泛应用
[5]
。 笔者首先给出 Catalan 数的 4 个组合模型, 然后利用迭代递推方法、
生成函数方法、 组合求差方法和一一映射方法给出了 Catalan 数的 4 种推导方法。
1 Catalan 数的四个经典组合模型
1畅1 凸多边形的三角剖分问题
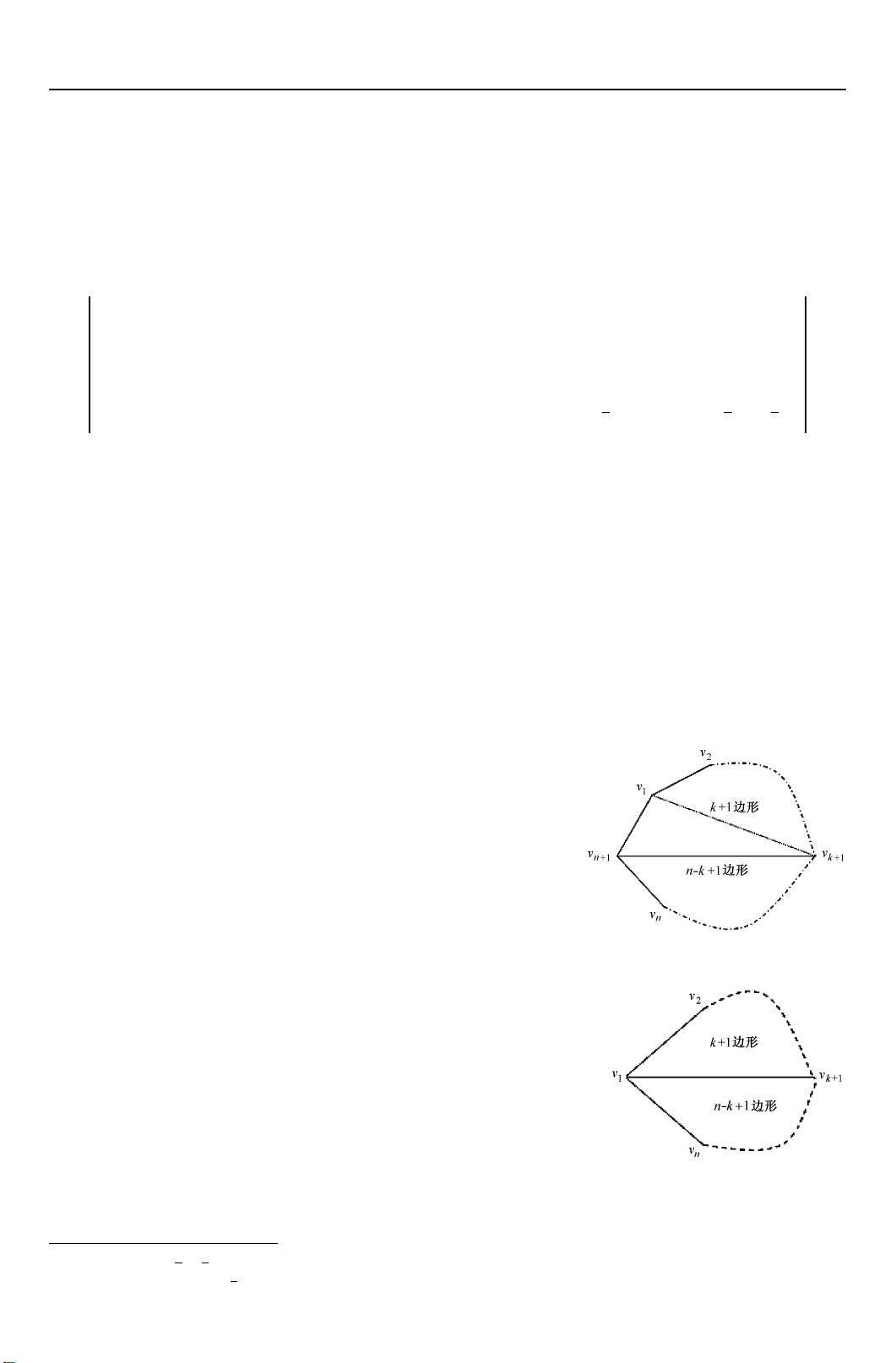
图 1 凸 n +1 边形的三角部分
一个凸 n +1 边形中可以最多画出 n -2 条两两不相交的对角
线,这些对角线可将多边形分割成 n -1 个三角形区域,称此为多边
形的一种三角剖分。可能的三角剖分方法数 A
n
称为 Catalan 数。
显然 A
2
=1,A
3
=2,A
4
=5。对于一般的 n,作图1 所示的 n +1
边形,以 v
1
v
n +1
作为三角形的一条边,三角形的另一个顶点为 v
k +1
(k
=1,2,…,n -1),三角形 v
1
v
n +1
v
k +1
将 n +1 边形分割成一侧为 k +
1 边形,另一侧为 n -k +1 边形。根据乘法原理,以 v
1
v
n +1
v
k +1
为一剖
分三角形的剖分数为A
k
A
n -k
。由于 k =1,2,…,n -1 所得剖分各不相
同,根据加法原理,有:
图2 凸 n 边形三角剖分数之关系示意图
A
n
=
钞
n -1
k =1
A
k
A
n -k
(1)
因为 A
2
=1,补充定义 A
1
=1,可得 Catalan 数列{A
n
}
n≥1
。另外,
作图 2 所示的 n 边形,从 v
1
分别到n -3 个顶点{v
3
,v
4
,…,v
n -1
} 引出
n -3 条对角线,以 v
1
v
k +1
(k =2,3,…,n -2) 对角线为例,将 n 边形
分解为一侧为 k +1 边形,另一侧为 n -k +1 边形。因此以 v
1
v
k +1
为
剖分线的 n 边形的剖分数目应为A
k
A
n -k
(k =2,3,…,n -2)。对 k 的
取值求和得:
钞
n -2
k =2
A
k
A
n -k
。v
1
点改为 v
2
,v
3
,…,v
n
也有类似的结果。由于
每一条对角线有 2 个端点,而且每个剖分总有 n -3 条对角
·61·
:1嗦2嗾喹嗉帻噍04郟+9 啶喹囿唰唰啜嘧 嗳嗫.囗啶20郳郤郤2喑 嘟啻嘌嘌啾(嘣嗷辔嗬 喙)08200( 嘞郳200) 囗啶9嗒嗄嗦鄁郿长江大学学报 (自然科学版)
2008 年 12 月 第 5 卷 第 4 期: 理工
Journal of Yangtze University (Nat Sci Edit) Dec畅2008, Vol畅5 No畅4: Sci & Eng















