use the traditional experimental techniques for timely and sys-
tematically detecting miRNAs from a genome (Xuan et al., 2011).
Facing the avalanche of genome sequences generated in the
postgenomic age, it is imperative to develop computational
methods (Li et al., 2010) for detecting miRNAs according to their
sequence information alone.
At present, the most successful computational approaches in
this field were using the Kmer composition to represent RNA
samples (Wei et al., 2014). But the length of Kmers practically
really useful in this area is less than 6 nucleobases. This is because
any Kmers longer than that would result in using extremely high-
dimension vectors to represent the statistical samples (Chen et al.,
2014b, 2014a; Lin et al., 2014), leading to the “high-dimension
disaster” (Wang et al., 2008)oroverfitting problem that would
significantly reduce the deviation tolerance or cluster tolerant
capacity (Chou, 1999) so as to lower down the success rate of
prediction. However, the miRNAs can vary from 17 to 25 nucleo-
bases. Therefore, the Kmer approach can be only used to represent
the short-range or local information of miRNA sequences but not
their long-range or global information. Particularly, most of the
pre-miRNAs have the characteristic of stem-loop hairpin struc-
tures (Xue et al., 2005). In view of this, some novel approaches are
definitely needed to relax the aforementioned limitation imposed
on the length of Kmers for miRNA sequences. The present study
was initiated in an attempt to address these problems.
2. Methods
2.1. Benchmark dataset
The benchmark dataset
used in this study can be formulated
as
SS S 1
∪
=()
+−
where the positive subset
S
contains pre-miRNA samples only,
which were extracted from the latest version of miRBase (release
21: June 2014). Furthermore, the CD-HIT software (Li and Godzik,
2006; Li et al., 2009) was used to make sure that none of the pre-
miRNA samples included in
S
has
80
≥
pairwise sequence
identity to any other. By doing so, we finally obtained 1 612 pre-
miRNA samples for the positive subset
S
.
The negative subset
S
also contained 1 612 samples, which
were randomly picked from the 8489 false pre-miRNAs in (Xue
et al., 2005). Again, none of the negative samples included in
S
has
80
≥
pairwise sequence identity to any other.
Since the most stringent cutoff threshold for DNA sequences by
CD-HIT is 75%, to our best knowledge, the aforementioned
benchmark dataset is so far the most stringent and largest
benchmark dataset constructed for studying the prediction of pre-
miRNAs.
Also, as pointed out in a comprehensive review (Chou and
Shen, 2007), there is no need to separate a benchmark dataset into
a training dataset and a testing dataset if a prediction method is to
be validated by the jackknife or subsampling (K-fold) cross-vali-
dation since the outcome thus obtained is actually from a com-
bination of many different independent dataset tests.
The benchmark dataset
as well as its subsets
S
and
S
, along
with the corresponding detailed sequences are given in Support-
ing information S1.
As pointed in Chou (2011) and concurred in a series of recent
publications (see, e.g., Chen et al., 2012; Min and Xiao, 2013; Xiao
et al., 2013a, 2015; Xu et al., 2013b, 2014b; Liu et al., 2014a, 2015a;
Qiu et al., 2014, 2015; Jia et al., 2015), one of the keys in success-
fully developing a sequence-based statistical predictor is how to
effectively formulate the sequence samples concerned with an
effective mathematical expression that can truly capture their
intrinsic correlation with the target to be predicted. Below we are
to address this problem.
2.2. Use degenerate Kmer composition to represent RNA samples
Suppose an RNA sequence R with L nucleobases (nitrogenous
bases or nucleic acid residues); i.e.,
R BBBBRBB B
2
L1234 567
=⋯
()
where
BAadenineCcytosine
Gguanine Uuracil
3
i
{}
∈( )( )
()()
()
denotes the nucleobase at sequence position
iL1,2, ,(= ⋯
.
The most straightforward method to represent an RNA sample
is just using its entire nucleobase sequence as shown in Eq. (2).In
order to identify whether the RNA sample belongs to pre-miRNA
or false pre-miRNA, one may use various sequence-similarity-
search-tools, such as BLAST (Altschul et al., 1997; Schaffer et al.,
2001), to search RNA database for those sequences that have high
sequence similarity to the query RNA sample R. Subsequently, the
attributes of the RNAs thus found were used to deduce the attri-
bute concerned for R. Unfortunately, this kind of straightforward
sequential model, although quite intuitive and without missing
any of the sample's information, failed to work when it did not
have significant sequence similarity to any character-known RNA.
To overcome such a difficulty, one had to consider using non-
sequential or discrete vector models to formulate RNA samples.
Actually, the other important reasons to embrace the vector
models is that all the existing computational algorithms can only
handle vectors but not sequences, as elaborated in a recent paper
Chou (2015) .
Here we are to propose a completely different vector model to
represent RNA sample, as described below.
First of all, formulating the RNA sequence of Eq. (2) according
to its secondary structure derived from the Vienna RNA software
package (released 2.1.6) (Hofacker, 2003), we have
R 4
L12 34 56 7
=ΨΨΨΨΨΨΨ ⋯Ψ ( )
where
1
denotes the secondary structure state of B
1
,
2
the
structure state of B
2
, and so forth. They can be any of the following
seven structure states; i.e.,
A, C, G, U, A U, G C, U G 5
i
Ψ∈{ − − − } ( )
where A, C, G, U represent the structure states of the four unpaired
nucleobases, while A–U, G–C, U–G represent the structure states of
the three paired bases. Note that, in order to reduce computational
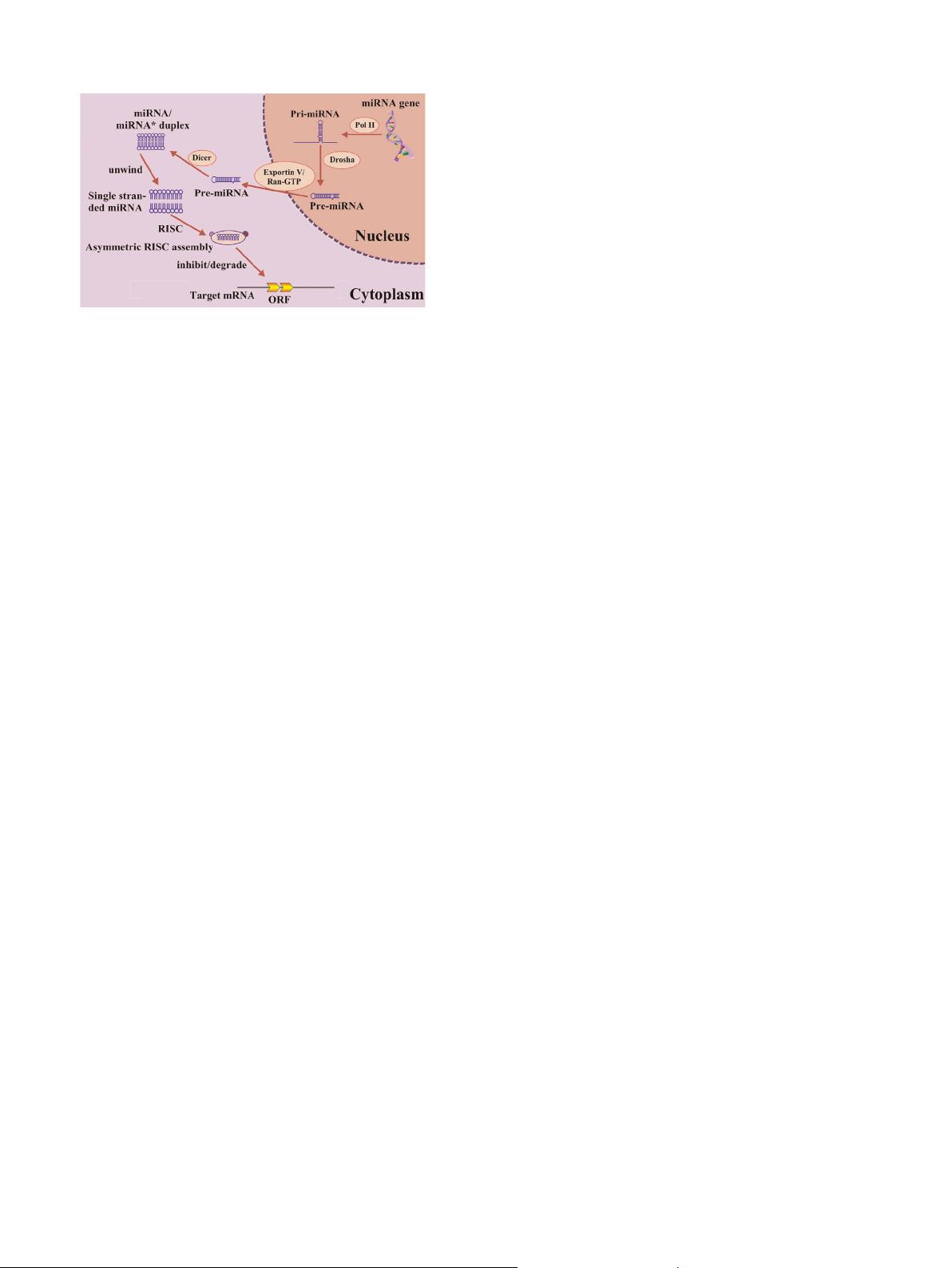
Fig. 1. MicroRNAs (miRNAs) are small single-strand and non-coding RNAs
(ncRNAs), which play important roles in gene regulation by targeting messenger
RNAs (mRNAs) for cleavage or translational repression.
B. Liu et al. / Journal of Theoretical Biology 385 (2015) 153– 159154



 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功