收稿日期 :2004唱09唱16 ;修改稿收到日期 :2005唱09唱19畅
基金项目 :国家自然科学基金(10202013 ) ;上海市高校优秀青年
教师后备人选资助项目 畅
作者简介 :贺远松
倡
(1975唱) ,男 ,硕士 ;
唐文勇(1970唱) ,男 ,博士 ,副教授 ;
张圣坤(1942唱) ,男 ,教授 ,博士生导师 畅
第23卷第6期
2006 年 12 月
计 算 力 学 学 报
Chinese Journal of Computational Mechanics
Vol .23 ,No .6
December 2006
文章编号 :1007唱4708(2006)06唱0743唱06
含 初 缺 陷 裂 纹 损 伤 梁 的 冲 击 动 力 屈 曲
贺远松
倡
, 唐文勇 , 张圣坤
(上海交通大学 海洋工程国家重点实验室 ,上海 200030)
摘 要 :由 Hamilton 原理导出考虑初始缺陷及横向剪切变形时裂纹梁的动力屈曲控制方程 ;应用断裂力学中常
用的线弹簧模型将裂纹引入到屈曲控制方程中 ;基于 B唱R 动力屈曲判断准则 ,采用数值方法求解了受轴向冲击
载荷作用时裂纹梁的动力屈曲 ;对比讨论了不同冲击速度 、初始几何缺陷大小以及分布形式等因素对梁冲击动
力屈曲的影响 。
关键词 :动力屈曲 ;裂纹梁 ;初缺陷 ;冲击
中图分类号 :O347 .2 文献标识码 :A
1 引 言
在结构的冲击动力屈曲研究领域中 ,梁结构的
轴向冲击动力屈曲分析主要针对含初缺陷但无裂
纹的金属材料梁 。 近年来 ,大批国内外学者在经典
理论的基础上对梁结构的动力屈曲问题进行了研
究 。 国内韩强
[1]
,刘书田
[2]
和龚良贵
[3]
等人采用小
参数的摄动法和变分法分析讨论了弹性直杆在冲
击载荷下的动力屈曲问题 ,研究中多不考虑初始缺
陷的影响 ,主要考虑了由于轴向应力波的传播而引
起的局部屈曲问题 。 另外 ,徐新生
[4]
,韩强
[5]
,翁徽
赣
[6]
和王刚
[7]
等人在考虑应力波的传播与反射而
引起的整体屈曲的情况下 ,分析了杆的弹塑性冲击
屈曲问题 。 U
瞕
lo Lepik
[8]
应用 Hamilton 原理从理
论上研究了低速冲击下的弹塑性梁的动力屈曲问
题 ,他 侧 重 分 析 了 初 缺 陷 对 动 力 屈 曲 的 影 响 。
Kenny
[9唱11]
等人针对含初缺陷细长杆受轴向冲击的
动力屈曲 ,对比分析了有限元分析 、数值计算和实
验结果 。
然而 ,由于在制造和运输等过程中 ,不可避免
地会使结构的内部或表面产生微小的缺陷 ,这些缺
陷会不断扩展和合并 ,形成宏观裂纹 。 裂纹在外部
载荷尤其是各种冲击载荷的作用下 ,最终可能导致
构件或结构在更短的时间内发生动力屈曲 ,甚至断
裂破坏 。 所以 ,在研究结构的动力屈曲问题时 ,考
虑裂纹等损伤的存在对结构动力屈曲性能的影响
尤为重要的 。 本文主要针对存在裂纹损伤梁的动
力屈曲进行分析 。
2 分析模型及非线性动力方程的推导
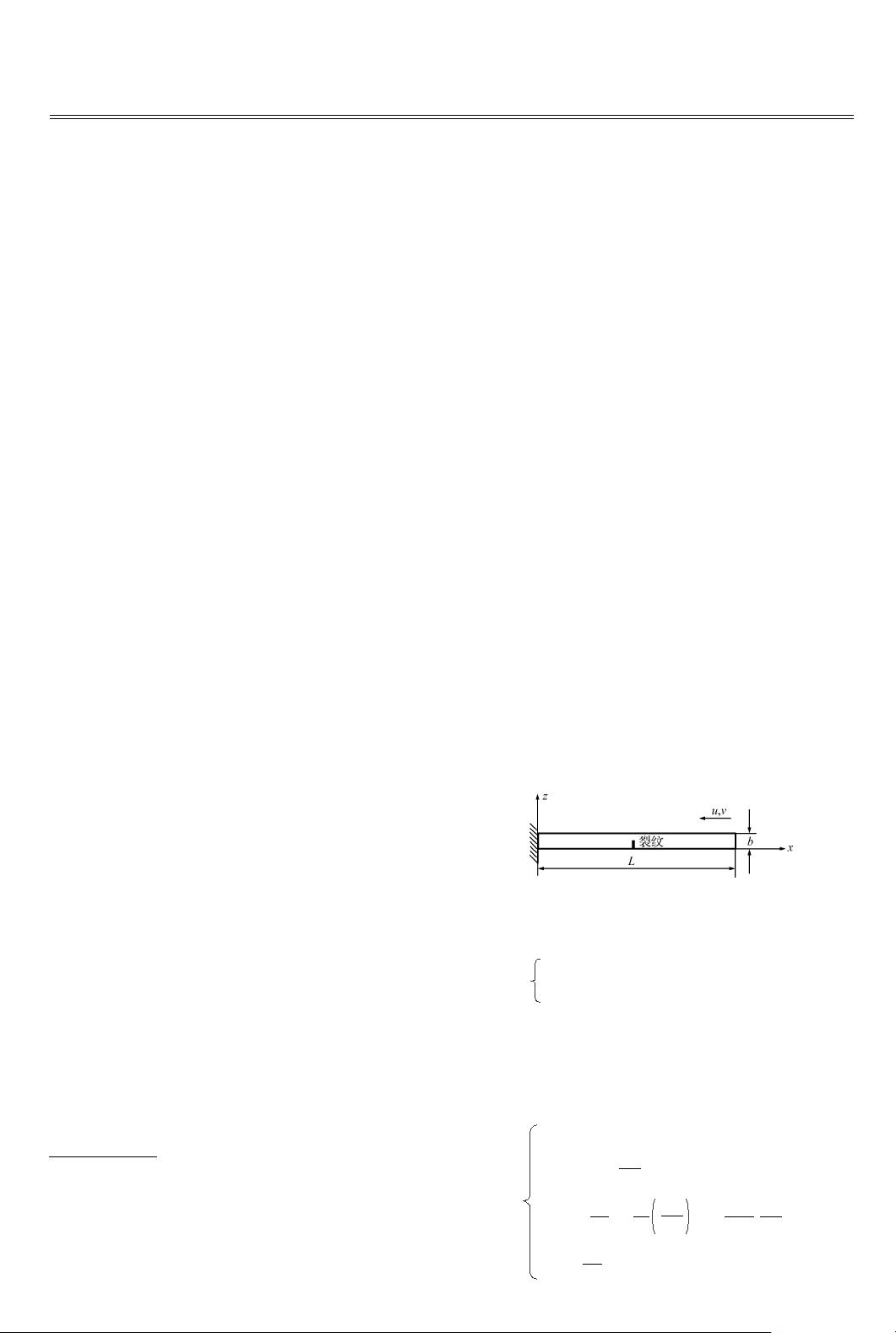
如图 1 所示的裂纹梁 ,一端固定 ,另一端在轴
向压缩载荷作用下以速度 v 运动 ,设梁长度为 L ,
高度为 h 。采用一阶剪切变形理论 ,梁的位移场可
设为
图 1 受冲击载荷作用的裂纹梁
Fig .1 A cracked beam subject to axial impact
u
-
(x ,z ,t) = u(x ,t) + z
α
(x ,t)
w
-
(x ,z ,t) = w(x ,t)
(1)
式中 u和 w 分别为梁中面轴向及横向位移 ,
α
为梁
中面法线绕
y
轴的转角 。包含初始几何缺陷的几何
关系及中面应变 、曲率为
[13]
ε
x
=
ε
(0)
x
+
z k
x
γ
x z
=
α
+
抄w
抄 x
ε
(0)
x
=
抄u
抄 x
+
1
2
抄w
抄 x
2
+
抄w
0
抄 x
抄w
抄 x
k
x
=
抄
α
抄 x
(2)