没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论

JHEP01(2017)074
Published for SISSA by Springer
Received: November 30, 2016
Accepted: January 10, 2017
Published: January 17, 2017
Massive three-loop form factor in the planar limit
Johannes Henn,
a
Alexander V. Smirnov,
b
Vladimir A. Smirnov
c,d
and
Matthias Steinhauser
d
a
PRISMA Cluster of Excellence, Johannes Gutenberg University,
Staudingerweg 9, 55099 Mainz, Germany
b
Research Computing Center, Moscow State University,
119991 Moscow, Russia
c
Skobeltsyn Institute of Nuclear Physics of Moscow State University,
119991 Moscow, Russia
d
Institut f¨ur Theoretische Teilchenphysik, Karlsruhe Institute of Technology (KIT),
Wolfgang-Gaede Straße 1, 76128 Karlsruhe, Germany
E-mail:
henn@uni-mainz.de, asmirnov80@gmail.com,
smirnov@theory.sinp.msu.ru, matthias.steinhauser@kit.edu
Abstract: We compute the three-loop QCD corrections to the massive quark-anti-quark-
photon form factors F
1
and F
2
in the large-N
c
limit. The analytic results are expressed in
terms of Goncharov polylogarithms. This allows for a straightforward numerical evaluat i on.
We also derive se r i e s expansions, including power suppressed terms, for three k i ne mat i c
regions corresponding to small and large invariant masses of the photon momentum, and
small velocities of the heavy quarks.
Keywords: NLO Computations, QCD Phenomenology
ArXiv ePrint:
1611.07535
Open Access,
c
The Authors.
Article funded by SCOAP
3
.
doi:
10.1007/JHEP01(2017)074

JHEP01(2017)074
Contents
1 Introduction
1
2 Setup and calculation 3
3 Infrared divergences of massive form factors 4
4 Results 6
4.1 Structure of re sul t s for form factors 6
4.2 Analytical results 6
4.2.1 Low-energy: s ≪ m
2
or x → 1 6
4.2.2 High-energy: s ≪ m
2
or x → 0 8
4.2.3 Threshold: s → 4m
2
or x → −1 11
4.3 Numerical results 13
4.4 Checks 13
5 Conclusions and outlook 15
1 Introduction
Massive form factors are impor tant buil d i ng blocks for various physical quantities involving
heavy quarks. Among them are static quantities like anomalous m agnet i c moments but
also producti on cross sections and decay rates. Furthermore, form factors are the prime
examples for study i ng the infrared behaviour of QCD amplitudes.
We consider QCD corrections to the quark-photon vertex. The latter can be
parametrized as fol l ows,
V
µ
(q
1
, q
2
) = ¯u(q
1
)Γ
µ
(q
1
, q
2
)v(q
2
) , (1.1)
where the colour indices of the quarks are suppressed and ¯u(q
1
) and v(q
2
) are the spi nor s of
the quark and anti-quark, respectively. The momentum q
1
is incoming and q
2
is outgoing
with q
2
1
= q
2
2
= m
2
.
The vertex function Γ
µ
(q
1
, q
2
) can be decomposed into two scalar form factors which
are usually intro du ce d as
Γ
µ
(q
1
, q
2
) = Q
q
F
1
(q
2
)γ
µ
−
i
2m
F
2
(q
2
)σ
µν
q
ν
, (1.2)
where q = q
1
−q
2
is the out goi ng momentum of the photon and σ
µν
= i[γ
µ
, γ
ν
]/2. Q
q
is the
charge of the considered quark. F
1
and F
2
are often referred to as el ec tr i c and magnetic
form factors.
– 1 –
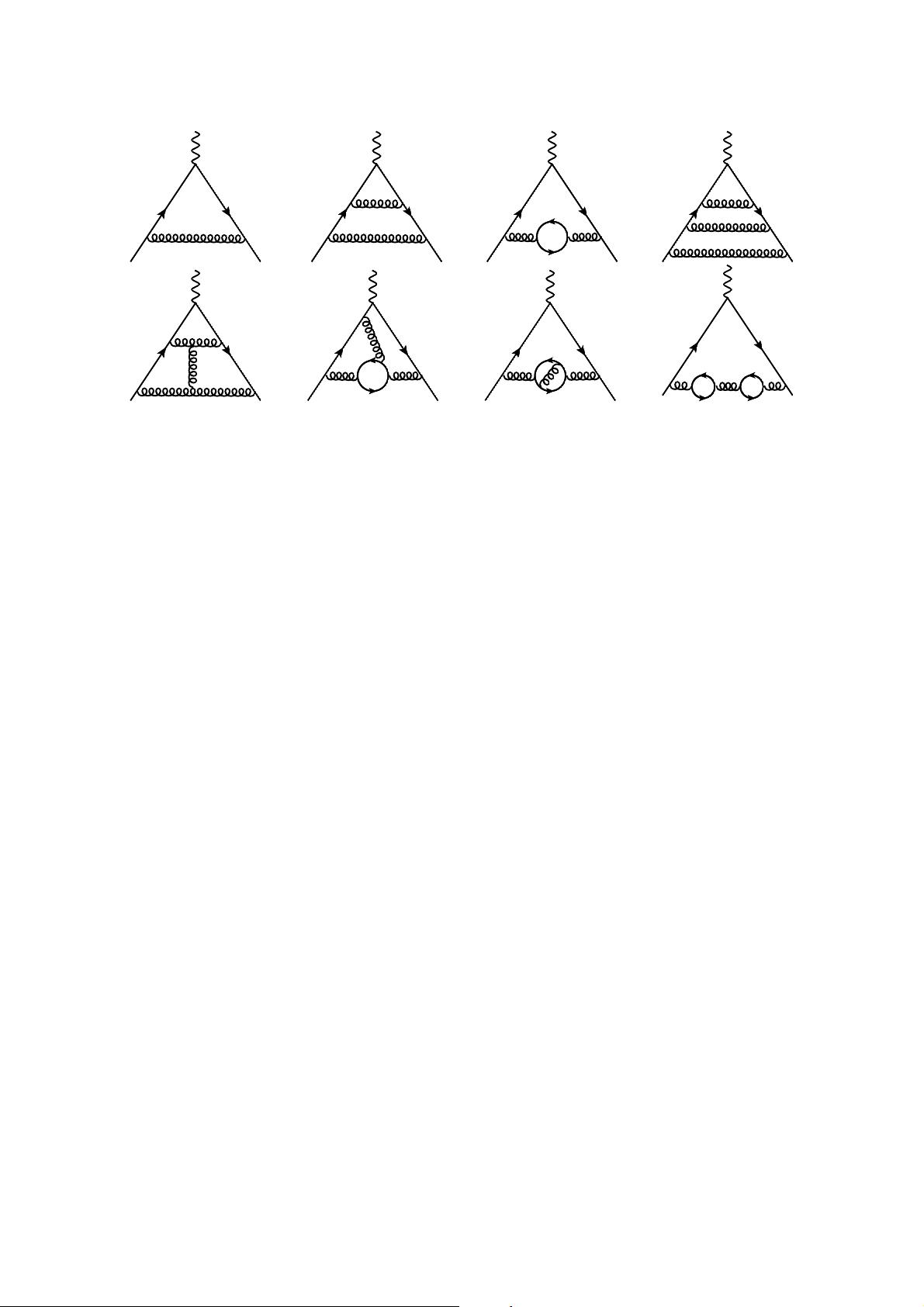
JHEP01(2017)074
Figure 1. Sample diagrams contributing to F
1
and F
2
at one-, two- and thr e e-l oop order. Solid,
curly and wavy lines represent quarks, gluons and photons, respectively. In our calculation the
closed fermion loops only involve massless quarks.
Sample Feynman diagrams can be found in figure 1. Two-loop QCD corr ec t i ons to the
electric and magnetic form factors for the heavy quark vector current have been computed
for the first time in ref. [
1] (axial vector and anomaly contributions have been consi d er e d
in [
2, 3]) where analytic results have been obtained. An independent cross check of t he two-
loop r e sul t s for F
1
and F
2
has been performe d in [
4] where also O(ǫ
2
) and O(ǫ) terms have
been added to the one- and two-loop results, respectively. The results have be e n used to
obtain predictions for the three-loop form factor F
1
in the high energy limit, by exploiting
evolution equations and the exponentiation of infrared divergences (see also ref. [
5] for
earlier considerations).
In this paper we compute the three-loop form factor in the planar limit, keeping the ex-
act mass dependence. After expanding our exact result for small quark masses we can com-
pare to the high-energy results of [
4] mentioned above, and complete them by determining
the unknown constants in the 1/ǫ and ǫ
0
part. We furthermore provide power-suppressed
terms.
Massive form factor s have infrared divergences that are well understood. After the
ultraviolet renormalization, all poles in dimensional regularization are given in terms of the
cusp anomalous dimension [
6, 7], and the beta function. The three-loop cusp anomalous
dimension was computed in re fs. [
8, 9]. By verifying the infrared pole structure at the
three-loop order, we provide a first independent check of the result of refs. [
8, 9] (in the
planar limit).
In the static limit, the infrared divergences dis appear, and F
1
and F
2
are finite. In
fact, F
1
vanishes and F
2
determines the anomalous magnetic moment of a heavy quark
which has been considered at two-loop order in ref. [
10]. A dedicated calculation at three
loops has been performed in ref. [
11] which serves as a welcome check for our ex ac t result
expanded for q
2
→ 0.
– 2 –
剩余18页未读,继续阅读
资源评论

weixin_38555350
- 粉丝: 2
- 资源: 931
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 【项目参考】MATLAB的手写汉字识别(第28期).zip
- 【项目参考】MATLAB的视频图像去雾(第28期).zip
- 【项目参考】MATLAB的小波变换dwt数字水印(第28期).zip
- 【项目参考】MATLAB的语音滤波设计(第28期).zip
- 【项目参考】MATLAB的运动行为检测(第28期).zip
- 【项目参考】MATLAB汉字识别(第28期).zip
- 【项目参考】MATLAB汉字语音识别(第28期).zip
- 【项目参考】MATLAB火焰识别系统设计(第28期).zip
- 【项目参考】MATLAB家居防火识别系统(第28期).zip
- 【项目参考】MATLAB基于DWT+SVD结合傅里叶变换的数字图像水印水印系统(第28期).zip
- 【项目参考】MATLAB火焰烟雾检测(第28期).zip
- 【项目参考】MATLAB教室人数统计(第28期).zip
- 【项目参考】MATLAB交通道路标识识别(第28期).zip
- 【项目参考】MATLAB金属表面缺陷分析(第28期).zip
- 【项目参考】MATLAB考勤系统设计(第28期).zip
- 【项目参考】MATLAB口罩识别(第28期).zip
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功