通过有效的直方图修改对预测误差进行可逆图像水印

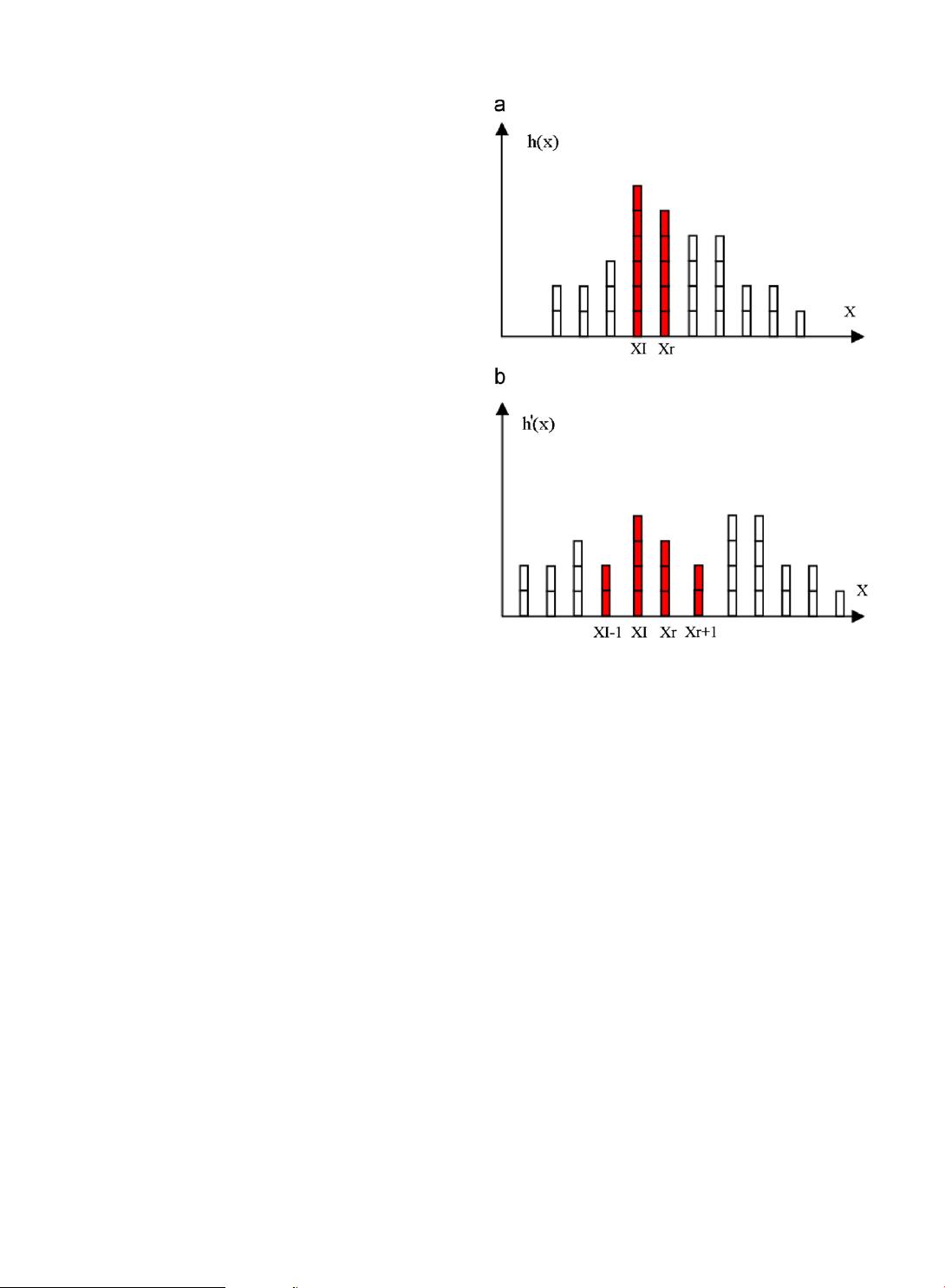
根据给定文件信息，本文将详细阐述以下几个核心知识点： 1. 可逆数据隐藏（Reversible Data Hiding） 可逆数据隐藏是指在数字媒体（如图像、音频、视频和3D模型）中隐藏信息，使得这些隐藏的数据不仅可以被提取出来，而且在提取后，原始数据可以完全恢复的技术。这种技术特别适用于那些不允许信息损失的应用场景，例如医疗和卫星图像。 2. 预测误差（Prediction Errors） 预测误差是指在可逆数据隐藏算法中，通过某种预测模型对原始数据（比如图像的像素值）进行预测后，实际值与预测值之间的差异。预测误差可以用于嵌入额外的数据信息，同时又能在之后被准确还原，以保持数据的完整性。 3. 直方图修改（Histogram Modification） 直方图修改是一种图像处理技术，通过对图像的直方图进行操作，使得图像的某些特性发生变化。在可逆数据隐藏中，直方图修改用于在不影响图像质量的前提下，找到适合嵌入数据的区域，从而实现数据的嵌入。 4. 效率（Efficiency） 效率在可逆数据隐藏的上下文中指的是算法对于直方图修改过程的执行速度和对原始数据的保护能力。一个高效的算法可以快速准确地嵌入大量数据，同时保持图像的原有内容不被破坏。 5. 像素值预处理（Pixel Value Pre-processing） 在数据嵌入之前对像素值进行预处理是为了防止在修改直方图时产生像素值的溢出（overflow）或下溢（underflow）。这一步骤对于保持原始图像的质量是至关重要的。 6. 预测模式（Prediction Modes） 本文提出了在四种不同的预测模式下，每种模式都能从宿主图像中产生大量预测误差。所有这四种模式的组合能够生成多个直方图对，以便进行有效的数据嵌入。 7. 数据嵌入（Data Embedding） 数据嵌入是在可逆数据隐藏过程中将隐藏信息融入到原始媒体中的步骤。在本研究中，通过使用一种新的预测方案，对预测误差进行研究，并采用多种直方图对进行序列化数据嵌入。 8. 盲检测（Blind Detection） 盲检测指的是在不知道原始图像的情况下提取和恢复隐藏信息的能力。本研究通过将预先计算的位置图和其他辅助信息嵌入到带水印的图像中，实现了盲检测和数据恢复。 9. 实验结果（Experimental Results） 文中提到了在多种测试图像上得到了令人满意的结果。与现有算法相比，在高有效载荷数据隐藏的条件下，本算法能够更好地保护图像内容。 10. 位置图（Location Map） 位置图是嵌入到带水印图像中的一组预先计算的信息，用于在数据提取时指导隐藏数据的搜索位置，它是实现盲提取的关键。 总结来说，本文研究的是一项有关可逆图像水印技术的创新方法。通过高效地修改直方图对预测误差进行数据嵌入，并通过盲检测技术实现数据的提取和原始图像的完全恢复。这项技术在医学和卫星图像等要求无信息损失的应用领域中具有重要价值。研究成果通过实验验证了算法的有效性和实用性，并且与现有技术相比，保持了更好的图像内容。