L. Wang et al. / Signal Processing 143 (2018) 232–240 233
However, to localize all source images, sparse approximation of
the spatial spectrum of virtual sources has to be considered in a
huge expanded free-space. In other words, an large over-complete
dictionary should be constructed to allow for sparse representa-
tion, which would ultimately result in a problem with catastrophic
dimensionality [13,14] . If the number of sources are known a priori,
it is possible to solve effectively the sparse recovery problem with
huge dimensionality by greedy algorithms. In practice, the source
number is practically unknown, the huge dimensionality will be
problematic and induce high computational complexity. Moreover,
the accuracy of greedy algorithms is often very limited, which is
another drawback of the conventional approaches.
Since the reverberant field is modeled by a superposition of the
projections associated with the source images in [13] , a stronger
reverberant field would generate a higher order source images re-
quired by the image model technique. The discretized enclosure is
then accordingly expanded into a huge free-space. Our work is mo-
tivated by the major drawback of the induced huge dimensionality
in [13,14] . To reduce the size of the problem within the enclosure,
we merely discretize the inner planar area of the enclosure into
grids and construct the corresponding dictionary by calculating the
images of the microphone array rather than those of the potential
sound sources. In this way, the multi-path effect can be character-
ized by a weighted superposition of the media Green’s functions
with weights being the reflective energy ratios of different orders.
Since the reflective energy ratio is generally unknown, the prob-
lem can be formulated into a sparse signal recovery and paramet-
ric dictionary learning problem, which is a more elegant way of
solving the huge dimensionality issue. A sparse Bayesian method
is proposed to automatically localize the sources and estimate the
unknown parameter of the dictionary, which is facilitated by the
variational Bayesian Expectation and Maximization (VBEM) tech-
nique [19–21] . To the best of our knowledge, this work is the pio-
neering one in introducing the parametric dictionary to model an
unknown reverberant field in a statistical way. The joint sparsity in
frequency is exploited to further improve the localization and dic-
tionary learning performances. Numerical simulation results have
demonstrated that the proposed method achieve high resolution,
low computational complexity, low sidelobes and high robustness
for multiple sources.
The rest of the paper is organized as follows. In Section 2 , the
sparse signal model will be formulated and the corresponding dic-
tionaries will be constructed. The source localization under strong
reverberant environment is formulated as a parametric Bayesian
dictionary learning problem in Section 3 . In Section 4 , numerical
simulation results will be presented to demonstrate the effective-
ness of the proposed method. Section 5 concludes the paper.
2. Sparse signal model
Suppose the sources are located on a two-dimensional plane in
a rectangular room with finite impedance walls and the measure-
ments obtained with a linear microphone array of M sensors are
transformed into the spatial-spectral domain. The point source-to-
microphone impulse responses of the room considering the mul-
tipath effect can be calculated based on the image model [13] ,
where each reflective wave can be treated as a signal coming from
a virtual source with a power equal to the reflective energy ratio
of the wall. The image method is an example of simplified ray-
based modeling of room reverberation where specular reflections
are considered. Such a simplification is justifiable when the diffrac-
tion and its interference effects found in wave propagation are in-
significant. For example, the wavelength of the sound is small com-
pared to the dimensions of the reflecting surfaces in the room and
large compared to any structural details or surface texture, which
is generally the case for ordinary rooms. By discretizing the inner
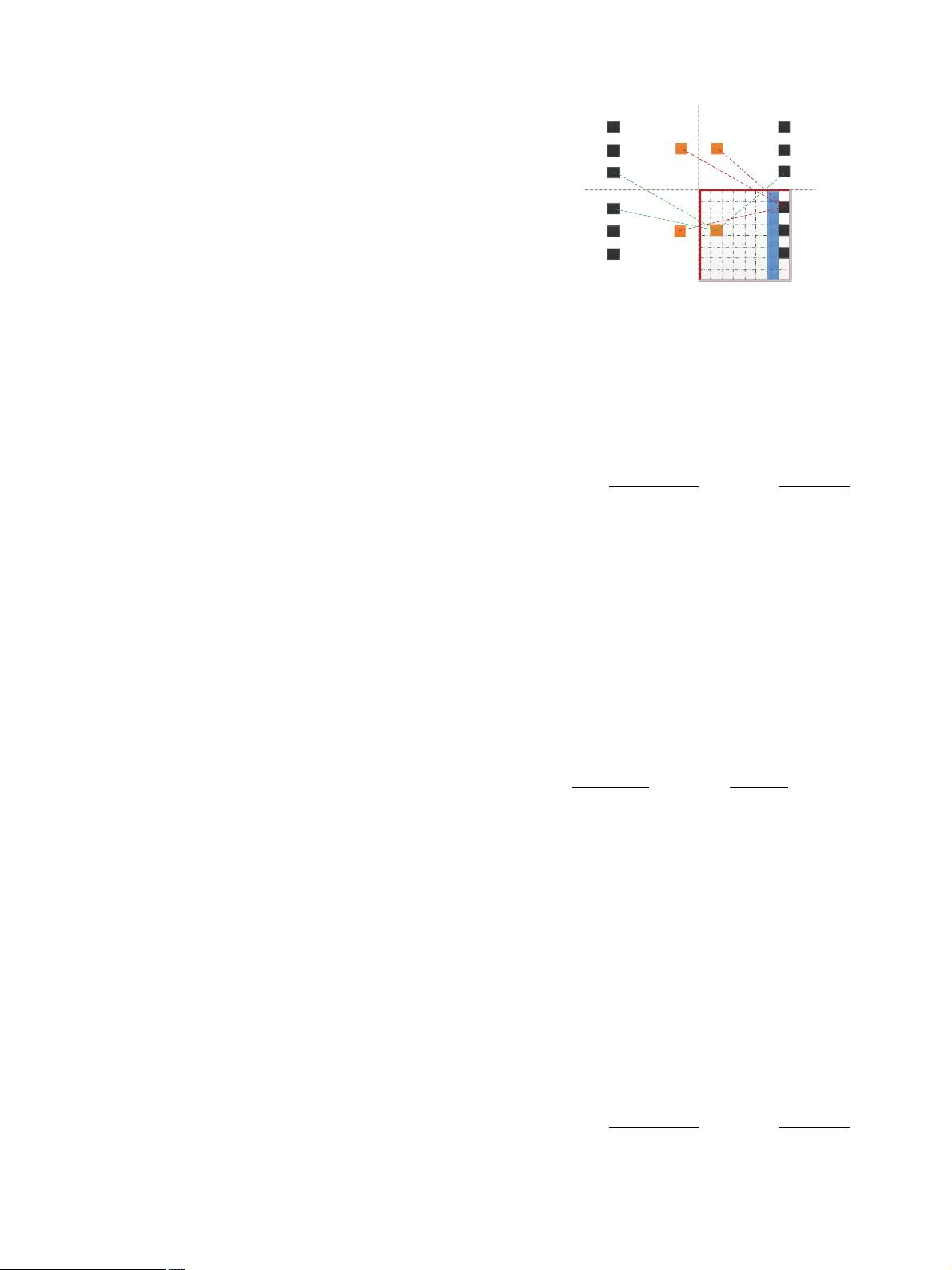
Microphone array
image 3
Source
image2
Microphone array
image 2
Microphone array
Microphone array
image 1
Source
image3
Source
image1
Fig. 1. The illustration of the equivalence. Without loss of generality, two perpen-
dicular walls marked in red line are considered. The inner plane containing the
actual sources is divided into grids. (For interpretation of the references to color in
this figure legend, the reader is referred to the web version
of this article.)
planar area of the enclosure into N grids, the projections of source
located at cell n and received by microphone at grid m , can be
characterized by the media Green’s function
y
f
(
m, n
)
= x
f
R
γ =0
β
γ
4 π
r
m
− s
n,γ
exp
− j2 π f
r
m
− s
n,γ
c
, (1)
where s
n, γ
represents the location of the γ th virtual source cor-
responding to the actual source located at cell n with the reflec-
tive energy ratio of β
γ
; R is the number of source images; c is the
speed of sound; and x
f
is the source amplitude of frequency f .
2.1. Dictionary constructed in [13]
In [13] , the N -cell grid of the room is expanded into N
g
-cell
free-space to contain all the active actual-virtual sources. Subse-
quently, a free-space propagation model with R = 0 in Eq. (1) , is
considered for the projection between N
g
potential source loca-
tions and M microphone positions. Consequently, a dictionary D
f
of size M × N
g
can be constructed with its element d
f
( m, n ) given
by
d
f
(
m, n
)
=
1
4 π
r
m
− s
n
exp
− j2 π f
r
m
− s
n
c
,
where n = 1 , 2 , ··· , N
g
. Set
{
s
n
}
N
g
n =1
contains all sources and their
image sources in a large expanded free space. If each source has
R images, N
g
should be equal to (R + 1) N. A stronger reverberant
field would generally require a larger R . A moderate reverberant
strength in practice could result in a N
g
much larger than N , ulti-
mately leading to computationally expensive sparse recovery pro-
cedures. It should be noted that a large N
g
probably result in an
unsolvable sparse recovery problem as will demonstrated later in
Section 4 .
2.2. Proposed parametric dictionary construction
In this paper, to restrict the problem size to N , a parameterized
dictionary of size M × N is constructed merely on the inner grids of
the enclosure. Using the equality
r
m
− s
n,γ
=
s
n
− r
m,γ
, pro-
jections in Eq. (1) can be equivalently written as
y
f
(
m, n
)
= x
f
R
γ =0
β
γ
4 π
s
n
− r
m,γ
exp
− j2 π f
s
n
− r
m,γ
c
(2)
where r
m, γ
is the γ th image of the microphone m . The equiva-
lence is illustrated in Fig. 1 . Notably, the distance between the γ th



 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功