
On the Optimal Provider Selection for Repair in Distributed Storage System 507
information created in 2015 and 8.6 Zettabytes of data center traffic by 2018 [1].
Therefore, many large-scale DSSs, e.g., Google File System [2], Azure [3], are
widely used for achieving high reliability by storing the data redundantly over
multiple unreliable storage servers.
Reliability is one of the basic requirements for these DSSs that users can
get data anywhere anytime. The traditional methods for providing reliability in
DSSs include replication and Reed-Solomon codes [4]. In 2000, NC was proposed
to increase the throughput of the network, balance network load and so on [5].
It has been proved distributed storage applications can achieve good benefits
with NC [6]. When using NC, it keeps the MDS property of erasure code that
the original file is divided into k packets, then encoded into n coded packets [7].
Users can recover the original file by any set of k coded packets among n coded
packets. Therefore, more and more researchers pay attention on NC in DSS.
Although NC can improve storage reliability, the data of distributed storage
systems is prone to be damaged, such as an outage of the server, invasion by
the hackers, disk damaged. To keep the same level of reliability, when a server
fails or leaves the system, a new server has to join the system and accesses
existing servers to regenerate the lost data, which leads to repair bandwidth
consumption and regeneration time. Based on the ideas of NC, the functional
minimum storage regeneration (FMSR) codes have been proposed to minimize
the repair bandwidth or regeneration time in DSS [8,9].
Although FMSR code can significantly minimize repair bandwidth, it cannot
ensure that the regeneration time is minimized. In order to reduce the regener-
ation time, Li et al. proposed a tree-structured data regeneration in the hetero-
geneous network [10,11]. Most of current studies focus on obtaining data from
multiple surviving servers to regenerate the lost data under the condition that
the bandwidth of the path between each servers and the new comer is given.
However, each link in physical network may be shared by multiple paths, which
means the bandwidth of each link should be shared between different paths.
Therefore, in practice, the bandwidth of the routing path from each selected
server, i.e., provider, to the new comer may not be achieved.
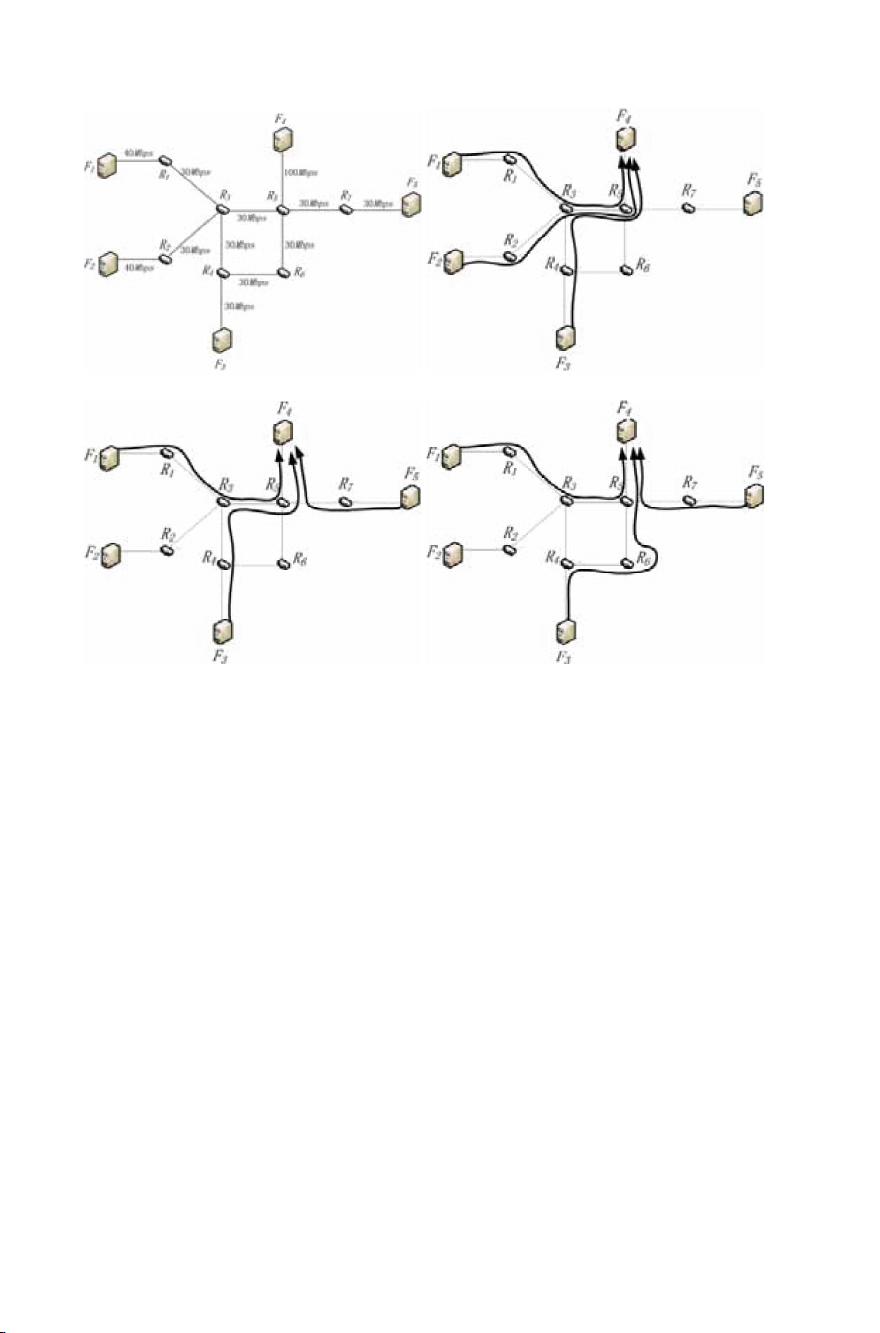
Next, we introduce an example that shows the effect for regenerating the
lost data by selecting a given number of servers as the providers and routing
paths from the providers to the new comer. Figure 1(a) gives the original network
topology and includes routers denoted as R
j
and storage servers denoted as F
i
.In
this example, each server F
i
stores different coded packets of the same file. When
F
4
is unavailable, to keep the same level of reliability, a new server should be
installed to replace F
4
and acquire data packets from multiple available storage
servers to regenerate the lost data. Therefore, in this example, we also denote the
new comer as F
4
. We assume the number of providers is 3, which is denoted as d
in the rest of the paper and the size of the file is M = 300 Mb. With the minimum-
storage regenerating code [12,13], each server storages α = M/k = 150 Mb
data and F
4
needs to download β = α/(d − k +1) = 75Mb data from each
provider. The bandwidths of the links range from 30 Mbps to 100 Mbps.As
shown in Fig. 1(a), the maximum transmission rate from each storage server to



 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功