令人兴奋的LLM几何资源-CSDN文库

Open

Access

94 浏览量 2020-04-06 04:01:03 上传评论收藏 639KB PDF 举报

资源推荐

资源详情

资源评论

JHEP07(2018)146

Published for SISSA by Springer

Received: June 22, 2018

Accepted: July 17, 2018

Published: July 24, 2018

Exciting LLM geometries

Robert de Mello Koch,

a,b

Jia-Hui Huang

and Laila Tribelhorn

School of Physics and Telecommunication Engineering,

South China Normal University, Guangzhou 510006, China

National Institute for Theoretical Physics,

School of Physics and Mandelstam Institute for Theoretical Physics,

University of the Witwatersrand, Wits, 2050, South Africa

E-mail: robert@neo.phys.wits.ac.za, huangjh@m.scnu.edu.cn,

laila.tribelhorn@gmail.com

Abstract: We study excitations of LLM geometries. These geometries arise from the

backreaction of a condensate of giant gravitons. Excitations of the condensed branes are

open strings, which give rise to an emergent Yang-Mills theory at low energy. We study

the dynamics of the planar limit of these emergent gauge theories, accumulating evidence

that they are planar N = 4 super Yang-Mills. There are three observations supporting

this conclusion: (i) we argue for an isomorphism between the planar Hilbert space of the

original N = 4 super Yang-Mills and the planar Hilbert space of the emergent gauge

theory, (ii) we argue that the OPE coeﬃcients of the planar limit of the emergent gauge

theory vanish and (iii) we argue that the planar spectrum of anomalous dimensions of the

emergent gauge theory is that of planar N = 4 super Yang-Mills. Despite the fact that the

planar limit of the emergent gauge theory is planar N = 4 super Yang-Mills, we explain

why the emergent gauge theory is not N = 4 super Yang-Mills theory.

Keywords: 1/N Expansion, AdS-CFT Correspondence, Brane Dynamics in Gauge The-

ories, Gauge-gravity correspondence

ArXiv ePrint: 1806.06586

Open Access,

 The Authors.

Article funded by SCOAP

https://doi.org/10.1007/JHEP07(2018)146

JHEP07(2018)146

How much, if anything, of this story survives for string excitations of new geometries?

The geometries that we have in mind are the LLM geometries [9]. An LLM geometry is

dual to an operator with a dimension that grows as N

in the large N limit. Consequently,

correlators of operators with dimensions of order N

encode the physics of excitations of

these geometries. For operators with such a large dimension the planar approximation is

not justiﬁed [11]. Consequently, mixing between diﬀerent trace structures is not suppressed.

The identiﬁcation between single trace operators in the CFT and spin chain states is spoiled

and it seems that the link to an integrable spin chain is lost. In this introduction we will

give some physical arguments which suggest that, at least for a subset of excitations, this

is not the case. The rest of the paper then carries out detailed CFT computations that

conﬁrm the details of this physical picture.

The LLM geometries are dual to a 1/2 BPS sector of the CFT. This 1/2 BPS sector

contains all gauge invariant operators built from a single complex matrix Z. Since we study

single matrix dynamics, there is a simple free fermion description, obtained by working in

terms of the eigenvalues of Z [12, 13]. There is also a closely related description which

employs Schur polynomials in Z [13, 14]. We mainly use this second description as we

know how to generalize it when including more matrices [15, 16]. This is needed when

studying small ﬂuctuations of the LLM geometries. A Schur polynomial dual to an LLM

geometry is labeled by a Young diagram with order N

boxes [9]. An operator dual to a

smooth supergravity geometry has a Young diagram with O(1) corners and the distance

between any two adjacent corners (that is, the number of rows or columns ending on the

side between the two corners) is order N. The string theory understanding of this geometry

is that it is the state obtained from back reaction of condensed giant gravitons [17–19]. The

translation between the CFT and string theory descriptions is direct: we read the rows of

the Young diagram as dual giant gravitons or the columns as giant gravitons [13].

To excite the geometry in the CFT description, add boxes at a particular corner of

the Young diagram describing the LLM geometry [20–22]. In string theory we understand

this as exciting the giants that condensed to produce the geometry. The description of

worldvolume excitations of these D3 brane giant gravitons is in terms of some open string

ﬁeld theory whose low energy limit gives rise to a new emergent Yang-Mills theory [23,

24]. Relative to the original Yang-Mills theory we started with, the space of the giant’s

worldvolume is an emergent space. The new emergent Yang-Mills theory may itself have

a holographic description so we might have new holographic dualities in this large charge

limit [23].

The intuitive picture sketched above suggests that excitations arising from any partic-

ular corner give rise to a distinct super Yang-Mills theory. We will study the planar limit

of these emergent gauge theories, to provide detailed support for this intuition. To restrict

to the planar limit consider excitations with a bare dimension of at most O(

√

N), i.e. add

at most O(

√

N) boxes to any given corner. Concretely we will demonstrate three things

1. An isomorphism between the planar Hilbert space of the original N = 4 super Yang-

Mills theory and the planar Hilbert space of the emergent gauge theory arising at

a corner. When restricted to the 1/2 BPS sector, these Hilbert spaces are in fact a

generalization of the code subspaces constructed by [25] (see also [26–28]).

– 2 –

JHEP07(2018)146

2. Three point functions of operators in the planar emergent gauge theory vanish. We

demonstrate this in the free ﬁeld theory. In the planar limit of matrix models the

vanishing follows because to mix three single traces we have to break some index

loops which costs (at least) a factor of N. This is a general conclusion true for both

free and interacting matrix models. Consequently we conjecture that our free ﬁeld

theory result holds after interactions are turned on. Since operator product expansion

(OPE) coeﬃcients can be read from the three point functions, this implies the OPE

coeﬃcients of the planar emergent gauge theory vanish.

3. The correct spectrum of planar anomalous dimensions of the emergent gauge theory.

We know the planar spectrum of anomalous dimensions of N = 4 super Yang-Mills

theory. We ﬁnd the same spectrum for the emergent gauge theory. This demonstrates

integrability for the emergent gauge theories.

Notice that since any CFT is determined by its spectrum of anomalous dimensions

and OPE coeﬃcients, and that in the strict planar limit all OPE coeﬃcients vanish, this

demonstrates that the planar limit of the emergent gauge theories are planar N = 4 super

Yang-Mills theory. We will see that although these diﬀerent emergent gauge theories all

share the same coupling constant (which is expected since this coupling is equal to the

string coupling constant of the original string theory on AdS

×S

), they generically have

distinct gauge groups U(N

eﬀ

). The rank of the gauge group N

eﬀ

receives contributions

both from the ﬂux of the original N D3 branes that gives rise to the N = 4 super Yang-

Mills theory we start with and from the giants which have condensed. By considering a

large charge state, its possible to have an emergent gauge theory with gauge group that

has rank larger than N.

What we are ﬁnding is that a subset of the excitations of large charge states of the N =

4 super Yang-Mills theory are equivalent to excitations of the vacuum. There are of course

excitations that go beyond the planar limit of the emergent gauge theory. The excitation

is constructed by adding boxes to the Young diagram describing the LLM geometry. We

might add so many boxes that we reach beyond two corners of the Young diagram deﬁning

the LLM geometry. The excitation is “too big” to sit on the Young diagram and in

this way we can detect features of the background Young diagram. These excitations are

obtained by adding ∼ N boxes and hence do not belong to the planar limit of the emergent

gauge theory - they are giant graviton like operators of the emergent theory. There are

also excitations constructed by adding order

√

N boxes, with the boxes added at diﬀerent

corners [21, 22, 45]. These (delocalized) states can be described as strings with magnon

excitations that stretch between two corners. We will show that at large N these states are

decoupled from (localized) states in the planar Hilbert space of the emergent gauge theory,

so that if we start from a state in the planar Hilbert space, the large N dynamics will not

take us out of this space. This is an important point to demonstrate since the coupling

of the planar Hilbert space of the emergent gauge theory to other degrees of freedom will

almost certainly ruin integrability.

The free fermion description of the system is a powerful description because of its

simplicity. The large charge state corresponds to exciting the fermions as illustrated in

– 3 –

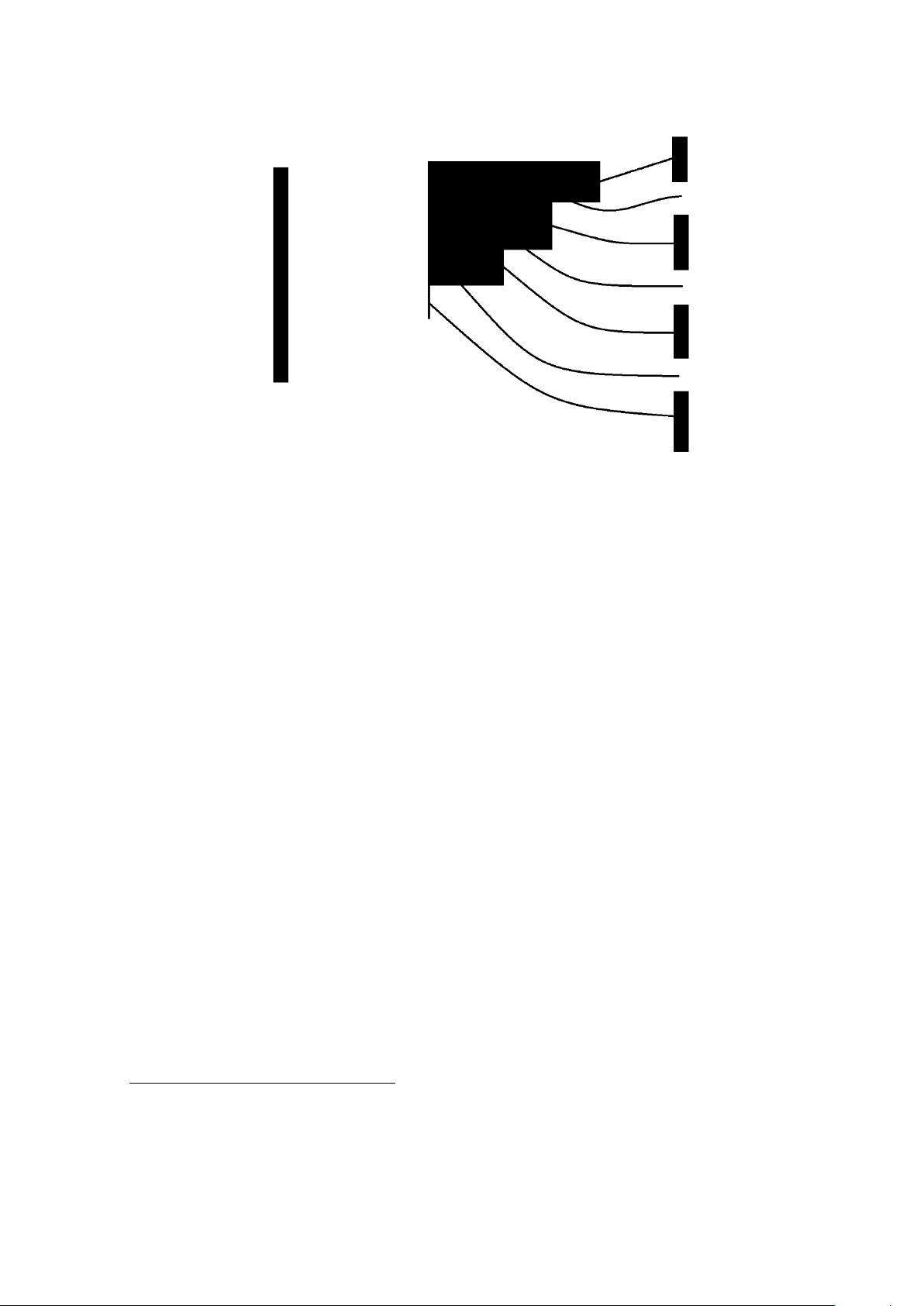
JHEP07(2018)146

Figure 1. The free fermion description of a state labeled by a Young diagram. On the left we have

the Fermi sea corresponding to the AdS

×S

geometry. The states are simply ﬁlled from the lowest

to highest energy with no unoccupied states. On the right, the Young diagram corresponding to a

particular LLM geometry is shown. Each vertical edge of the Young diagram maps into occupied

states while the horizontal edges map into unoccupied states. The number of fermions that were

not excited at all is equal to the number of rows with no boxes. Thus, the excited state has broken

the Fermi sea up into a series of occupied blocks.

ﬁgure 1. The idea that a subset of the excitations of large charge states of the CFT are

equivalent to excitations of the vacuum has a natural interpretation in this free fermion

language. We are saying that exciting any edge of the blocks appearing in the excited state

is equivalent to exciting the edge of the original Fermi sea. The only diﬀerence between the

diﬀerent blocks is their extent. By restricting to the planar limit we consider excitations

that are not able to detect that the Fermi sea is not inﬁnite, so the extent of each block

is irrelevant.

We will be using group representation theory methods to approach the problem of

computing correlators of operators with a bare dimension of order N

. This approach has

been developed in a series of articles [13, 15, 16, 29–38], which has developed a number of

bases for the local operators of the theory. These bases diagonalize the two point function

of the free theory to all orders in 1/N, and they mix weakly at weak coupling [30, 39, 40].

They therefore provide a very convenient tool with which to tackle the large N but non-

planar limit of the CFT.

The representation theory methods sum the complete set of ribbon graphs. In this

approach, operators are constructed using projection operators

of the symmetric group so

that the gauge invariant operators are labeled with irreducible representations of the group.

Summing the ribbon diagrams of the free theory becomes multiplying these projectors and

These operators are actually intertwiners since they map between diﬀerent copies of the representations

involved. For simplicity though the reader may think of them as projectors which are more familiar.

– 4 –

剩余39页未读，继续阅读

评论收藏

内容反馈

weixin_38544781

粉丝: 9
资源: 940

令人兴奋的LLM几何

LLM几何中各向异性最小曲面的全息纠缠熵

LLM几何中的纠缠阴影

初等几何教程（上册）（平面几何）.pdf

几何讲义++第一学期++解析几何.pdf

直观几何（希尔伯特）

Sketchpad几何画板工具包

黎曼几何引论 上册

几何图霸（三维几何图形绘制软件）

高等几何 周兴和 科学出版社

3基础几何学之二：向量几何，解析几何与球面几何

几何画板5.01 绿色

空间解析几何 苏步青

几何学教程立体几何卷.pdf

初等几何学习几何的书籍

计算几何 算法几何 程序

计算几何算法与应用计算几何算法与应用

《数学·统计学系列:几何变换与几何证题》作者: 萧振纲 出版年: 2010年

等几何分析-LSDYNA4

几何画板最强中文永久免费5.06版本安装包下载解压安装即可

几何画板课件350套.zip

微分几何讲义_陈省身

数论--计算几何（函数逼近论、微分几何、代数几何、计算数学特别是NC等形成的边缘学科

几何画板绿色版无毒完整

计算机辅助几何造型技术

解析几何_几何_matlab_解析几何_

几何画板5，几何画图好工具

信息几何-Information Geometry

几何基础 第二版 （希尔伯特）

代数几何武林秘籍 代数几何武林秘籍

丘成桐 微分几何 讲义

最新资源

黎曼几何引论上册

高等几何周兴和科学出版社

空间解析几何苏步青

计算几何算法几何程序

《数学·统计学系列:几何变换与几何证题》作者: 萧振纲出版年: 2010年

几何基础第二版（希尔伯特）

代数几何武林秘籍代数几何武林秘籍

丘成桐微分几何讲义