1077-2626 (c) 2015 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See
http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI
10.1109/TVCG.2015.2476788, IEEE Transactions on Visualization and Computer Graphics
JOURNAL OF IEEE TRANSACTIONS ON VISUALIZATION AND COMPUTER GRAPHICS, VOL. 13, NO. 9, SEPTEMBER 2015 1
Multiphase Interface Tracking with Fast
Semi-Lagrangian Contouring
Xiaosheng Li, Xiaowei He, Xuehui Liu, Jian J. Zhang, Baoquan Liu, and Enhua Wu
Abstract—We propose a semi-Lagrangian method for multiphase interface tracking. In contrast to previous methods, our method
maintains an explicit polygonal mesh, which is reconstructed from an unsigned distance function and an indicator function, to track the
interface of arbitrary number of phases. The surface mesh is reconstructed at each step using an efficient multiphase polygonization
procedure with precomputed stencils while the distance and indicator function are updated with an accurate semi-Lagrangian path
tracing from the meshes of the last step. Furthermore, we provide an adaptive data structure, multiphase distance tree, to accelerate
the updating of both the distance function and the indicator function. In addition, the adaptive structure also enables us to contour the
distance tree accurately with simple bisection techniques. The major advantage of our method is that it can easily handle topological
changes without ambiguities and preserve both the sharp features and the volume well. We will evaluate its efficiency, accuracy and
robustness in the results part with several examples.
Index Terms—multiphase interface tracking, semi-Lagrangian contouring, fluid simulation
!
1INTRODUCTION
P
YSICAL phenomena involving interconnected moving
interfaces are common in our daily life, including dry
foams, beer bubbles, and mixing of multiple immiscible flu-
ids. However, how to capture the motion of these interfaces
is challenging as their movements are often complex, and
include substantial topological changes. Various methods
have been proposed to track multiphase interfaces, mainly
including the front tracking method [1], the volume of fluid
method [2] and the level set method [3]. Unfortunately, as
the phase number increases, it remains a challenge for these
methods to robustly and accurately handle the wide range
of interface evolutions, especially at the degeneracies where
multiple interfaces meet.
Recently, Saye and Sethian [4] proposed an implicit
scheme, which is referred to as Voronoi Implicit Interface
Method (VIIM), to track multiphase interfaces based on
the combination of Voronoi diagrams and implicit level
set methods [3], [5]. Instead of using multiple level set
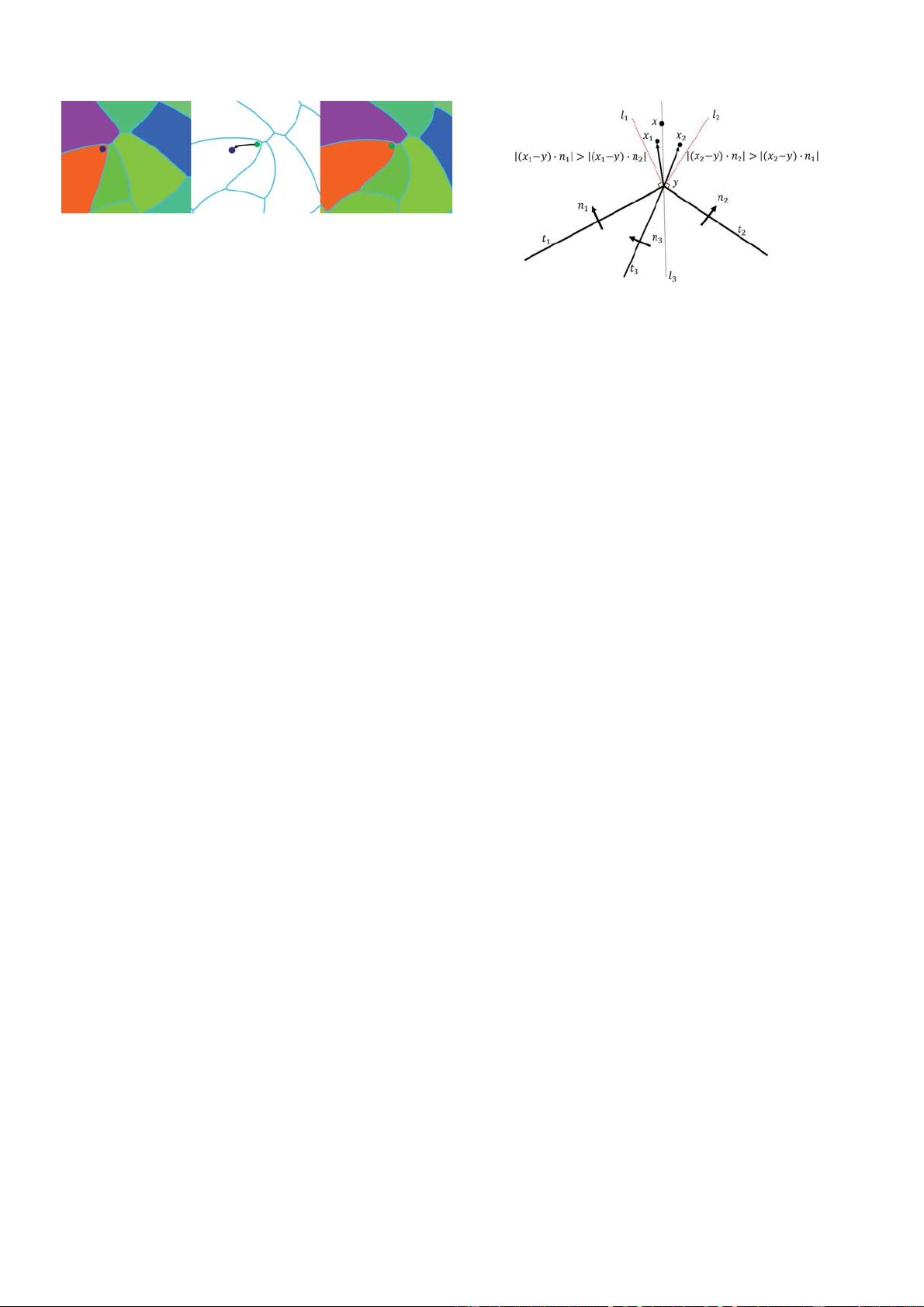
functions, the VIIM applies an unsigned level set distance
function together with a material indicator function to track
the entire multiphase system. Compared to the level set
methods, the VIIM can easily handle tens of thousands
of separate phases and the topological changes without
worrying about the memory overhead. For a more detailed
numerical analysis, we refer to Saye and Sethian’s recent
• X. Li and X. He is with the State Key Laboratory of Computer Science,
Institute of Software, Chinese Academy of Sciences and the University of
Chinese Academy of Sciences, Beijing, China, 100190.
E-mail: lixs@ios.ac.cn
• X. Liu is with the State Key Laboratory of Computer Science, Institute of
Software, Chinese Academy of Sciences.
• J. J. Zhang is with the National Centre for Computer Animation,
Bournemouth University.
• B. Liu is with the Department of Computer Science and Technology,
University of Bedfordshire.
• E. Wu is with the State Key Laboratory of Computer Sciences, Institute of
Software, Chinese Academy of Sciences and the University of Macau.
Manuscript received 2015; revised 2015.
work [6]. However, since the VIIM is built on the implicit
level set method, several disadvantages are inherited. First,
the VIIM suffers an excessive amount of volume loss in
under-resolved regions of the flow. Second, since the VIIM
relies on
-surface (whose distance value is ) to reconstruct
multiphase interfaces, thin features such as the interfacial
filaments and regions of high curvature will be smeared out.
Finally, it is also not clear how to extend the method to an
adaptive implementation as
is required to be constant over
the entire domain.
In this paper, we propose a new method which combines
the best properties of a standard VIIM and an explicit
contouring technique for improved accuracy and efficiency.
Along with an unsigned distance function and an indicator
function that are used to track the materials implicitly, we
introduce an extra surface mesh to denote where exactly
the interfaces are located at each time step. During the
advection, we first use the surface mesh at the previous
step as a reference to update the distance function and the
indicator function with a semi-Lagrangian scheme, and then
reconstruct the new surface mesh from the distance function
and the indicator function. To get an accurate estimation of
the distance function and the indicator function, we improve
the semi-Lagrangian contouring (SLC) method proposed by
Bargteil et al. [7] to make it suitable for multiphase interface
tracking. We also develop a fully adaptive scheme to make
the interface tracking as efficient as possible.
Our contributions in this paper include
• A material identification procedure to compute exact
indicator function at any point of the domain.
• A multiphase polygonization procedure combined
with bisection to contour the multiphase system.
• A multiphase distance tree structure to resolve the
distance function and indicator function efficiently.
By combining the best properties of VIIM and SLC, our
method is capable of tracking multiphase interfaces with
剩余13页未读，继续阅读
资源评论
