Achievinghighdiversityandmultiplexinggainsintheasynchronousparallelrelaynetwork资源-CSDN文库

研究论文

82 浏览量 2021-02-09 01:47:36 上传评论收藏 400KB PDF 举报

资源推荐

资源详情

资源评论

TRANSACTIONS ON EMERGING TELECOMMUNICATIONS TECHNOLOGIES

Trans. Emerging Tel. Tech.

2013; 24:232–243

Published online 12 February 2013 in Wiley Online Library (wileyonlinelibrary.com). DOI: 10.1002/ett.2618

RESEARCH ARTICLE

Achieving high diversity and multiplexing gains in the

asynchronous parallel relay network

Mingjun Dai

†

and Chi Wan Sung

College of Information Engineering (also with Shenzhen Key Lab of Advanced Communication and Information Processing),

Shenzhen University, Shenzhen, China

Dept. of Electronic Engineering, City University of Hong Kong, Hong Kong, China

ABSTRACT

A single source-destination pair communicating via a layer of parallel relay nodes under quasi-static slow fading environ-

ment is investigated. The time delays from the source to the destination via different relays are assumed to be different.

For such an asynchronous environment, a new transmission scheme is constructed so as to achieve better diversity-

multiplexing tradeoff (DMT). More speciﬁcally, both the source and the destination adopts orthogonal frequency division

multiplexing technique to solve the asynchronous problem; the relays cooperatively apply the distributed generalised

complex orthogonal design, a form of orthogonal space–time coding, for high-rate transmission. Each relay is assumed

to use the adaptive amplify-and-forward relaying strategy. To optimise its outage performance, a distributed on-off power

control rule applied to the relays is analytically derived and is proved to yield full spatial diversity order. Compared with

an existing protocol, our proposed scheme is shown to achieve the same DMT when there are four relay nodes and better

DMT when there are more. Besides, the DMT gap between our scheme and the existing one increases with the number of

*Correspondence

M. Dai, College of Information Engineering (also with Shenzhen Key Lab of Advanced Communication and Information Processing),

Shenzhen University, Shenzhen, China.

E-mail: mingjundai@hotmail.com



The work was partly performed when he was with City University of Hong Kong.

Received 26 September 2012; Revised 9 December 2012; Accepted 3 January 2013

1. INTRODUCTION

Space–time block codes (STBC), in particular, orthogonal

STBC (OSTBC), is an effective technique to harvest

spatial diversity for point-to-point multi-input multi-output

system [1]. It can also be applied to relay networks with

each relay acts as a virtual antenna. Cooperative spatial

diversity can then be achieved, assuming the signals trans-

mitted from the relays can be superimposed at the desti-

nation in a synchronised way [2–4]. In practice, however,

the time delays from the source to the destination via

different relays are different, as the relays are not collo-

cated. Therefore, it is important to consider asynchronous

relay nodes.

Full asynchronous cooperative diversity for a parallel

relay network with single source-destination pair has been

studied in [5–10]. The work in [5] requires feedback

from destination to relays. When a feedback channel

is not available, the use of space–time trellis coding

may be used [6], but its detection complexity is high.

Some other transmission schemes have also been proposed

in the literature, namely, time-reversal distributed OSTBC

(TR-DOSTBC) with decode-and-forward (DF) relay nodes

[7], orthogonal frequency division multiplexing (OFDM)-

DOSTBC with ﬁxed gain amplify-and-forward relay nodes

[8, 9] and shift-orthogonal STBC with either DF or FGAF

relay nodes [10]. In [7, 8], the proposed methods are

restricted to the case where there are only two relay nodes.

Although the schemes in [9, 10] are for more than two

relay nodes and are able to achieve full diversity, their

multiplexing gain is not high when the number of relay

nodes is large. In [11], the condition on the structure

of STBC to achieve full asynchronous diversity is iden-

tiﬁed. How to construct STBC that satisﬁes the condi-

tion, however, is not given. Besides, only the four group

decodable STBC is given, whose decoding complexity is

much higher than that of symbol-wise OSTBC. In [12],

the diversity-multiplexing tradeoff (DMT) in asynchronous

setting is analysed. Again, there is no explicit construc-

tion provided. Besides, the OFDM module is placed at

232

M. Dai and C. W. Sung

the relay nodes that is quite energy-consuming for low-

cost relay nodes. Regarding the forwarding strategies of the

relays, it is well known that DF suffers from high encoding-

decoding complexity [13], which increases energy con-

sumption. FGAF does not require decoding and is thus

simpler to implement. However, as the amplifying gain of

each relay is ﬁxed, it is possible that the transmit ampliﬁers

of the relay nodes are driven into saturation. In that case,

full diversity can no longer be guaranteed.

In this paper, we extend our work in [14], which can

only be applied to synchronous relay networks. We design

a new transmission scheme, which can achieve a good

DMT for asynchronous networks with large number of

relay nodes. In our design, we use the OFDM technology

to solve the asynchronisation problem. A high symbol-rate

DOSTBC matrix named distributed generalised complex

orthogonal design (DGCOD) matrix is adopted to provide

high multiplexing gain. We consider the use of adap-

tive amplify-and-forward (AAF), which is an AF scheme

whose amplifying factor is not ﬁxed. It avoids the ampliﬁer

saturation problem of FGAF. However, for AAF, it is

important to set the amplifying factor properly, for other-

wise, full diversity may be hampered [15]. We solve this

problem by deriving a power control law called on-off

power control (OOPC).

Our proposed scheme is attractive from a practical stand-

point, as the operations at each node is simple: The source

node performs fast fourier transform with cyclic preﬁx

(CP) addition. Each relay node performs either time rever-

sion or complex conjugate operation with simple OOPC.

Note that communication among relay nodes is not needed,

and the on-off decision is based only on local informa-

tion. The destination node performs fast fourier transform,

CP removal and orthogonalised fast symbol-wise detection

[16, 17]. Compared with the scheme in [9], our proposed

scheme achieves the same DMT when there are four relay

nodes and better DMT when there are more. Besides, the

gap between our scheme and that in [9] increases with the

number of relay nodes.

The rest of this paper is organised as follows: The

system model is presented in Section 2. Basic knowledge

on generalised orthogonal designs is given in Section 3.

The proposed scheme with corresponding power control

rule are illustrated in Sections 4 and 5, respectively. The

DMT comparison between our scheme with an existing

scheme is shown in Section 6. Finally, conclusion is drawn

in Section 7.

2. SYSTEM MODEL

We consider a single source communicating to a single

destination in a network over a layer of N parallel relay

nodes. There is no direct link from the source to the des-

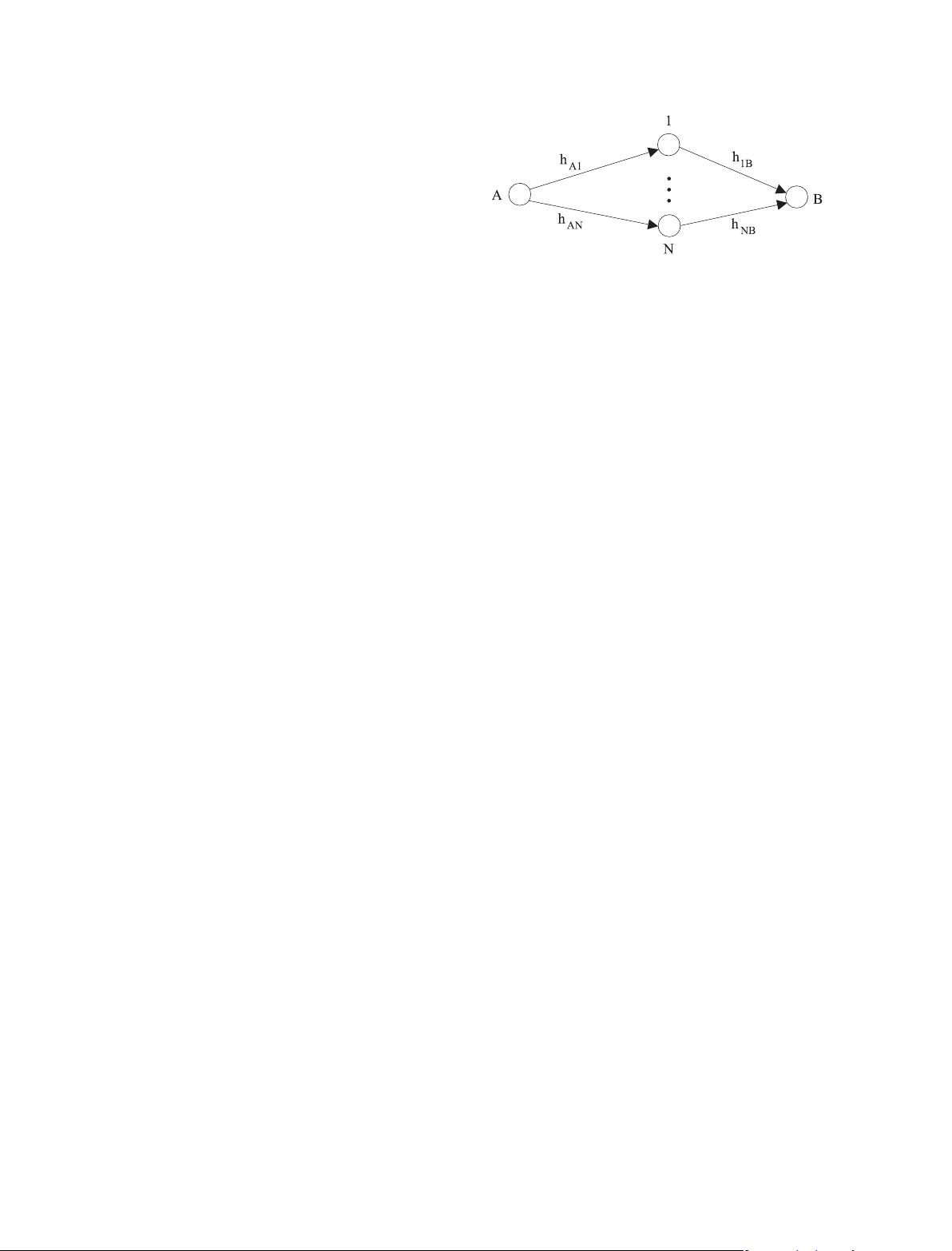
tination. As shown in Figure 1, source A has a single

transmit antenna, and destination B has a single receive

antenna. The N relays are respectively denoted as relay

i 2f1; 2;  ;Ng , N , each having a single antenna

Figure 1. The parallel relay network model.

that can transmit and receive in half-duplex manner. We

consider the slow-fading scenario where the link gains

are random but remain constant for a transmission block

of 2P transmission symbols, where the value of P is

determined in next section. Let h

and h

be the link

gains from source A to relay i and from relay i to des-

tination B, respectively, where i 2 N .Deﬁneh

the column vector .h

;  ;h

/,andh as the column

vector .h

;  ;h

/. We assume that

channel state information of a communication link is

available at its receiver but not at its transmitter. More

speciﬁcally, relay i knows h

, and the destination node

knows h

. Denote 

as the overall relative delay from

source A to destination B via relay i, which is known

by destination B, where ‘relative’ means relative to relay

node 1,thatis,

D 0 (We assume relay 1 has the shortest

delay.) and 

> 0 for i 2 N nf1g. For simplicity, 

’s are

assumed to be integers. We leave it as a future direction for



’s being real numbers.

Let

Œm denote the transmitted codeword from node i

at time instant m, i 2fAg

N ,

Œm and Nw

Œm denote

the received codeword and the thermal noise at node i at

time instant m, i 2fBg

N . The ﬁrst and second hop’s

channel’s input–output relationship are represented by the

following formulas:

Œm D h

Œm CNw

Œm for i 2 N (1)

Œm D

iD1

Œm C 

 CNw

Œm (2)

subject to the following power constraint: the power of

Œm, averaging over a transmission block of P symbol

times, is less than P

, and that of

Œm, averaging over

a transmission block of 2P symbol times, is less than P

for i 2 N . Note that the received signal at each relay

originates only from one source. We hence do not need to

consider the time delay in the ﬁrst hop. We further assume

that P

, P

and w

Œm; w

Œm  CN.0; 

/, i 2 N .

The instantaneous received signal-to-noise ratio (SNR) at

relay i is denoted by 

and is equal to jh

,where

SNR  , P

=

. The instantaneous received SNR at des-

tination B is denoted by 

.h/, whose value depends on

Trans. Emerging Tel. Tech.

DOI: 10.1002/ett

233

剩余11页未读，继续阅读

评论收藏

内容反馈

weixin_38508549

粉丝: 5
资源: 917

Achieving high diversity and multiplexing gains in the asynchron...

最新资源

Achieving high diversity and multiplexing gains in the asynchron...

Multi-operator resource sharing scenario in the context of IMT-advanced systems.pdf

Wireless Sensor Network-based Adaptive Vehicle Navigation in Multihop-Relay WiMAX Networks*

A utility-based capacity optimization framework for achieving cooperative diversity in the hierarchical converged heterogeneous wireless networks&amp;nbsp;

LINQ to Objects Using C# 4.0: Using and Extending LINQ to Objects and Parallel LINQ

network coding

Hands-On High Performance Programming with Qt 5-2019

Understanding UMTS Radio Network Modelling, Planning and Automated Optimisation

【13】Achieving Human Parity in Conversational Speech Recognition.pdf

Cloud and Fog Computing in 5G Mobile Networks-IET(2017).pdf

RetinaFace: Single-stage Dense Face Localisation in the Wild.pdf

Computer Organization and Design 完整版带目录

Achieving high energy density in PVDF-based polymer blends: suppression of early polarization saturation and enhancement of breakdown strength

Detection and Tracking of Moving Objects Using a Network of Laser Scanners

Achieving Data Access Control in Cloud Computing

IJPP-2009.pdfA Speculative and Adaptive MPI Rendezvous Protocol Over RDMA-enable

Management perception of innovation and its role in achieving competitive advantage

基于CORDIC的反正弦和反余弦计算的FPGA实现

BA无标度网络中的SIR模型

使用3DCNN和卷积LSTM进行手势识别学习时空特征

基于三次贝塞尔曲线的类汽车曲率连续路径平滑

基于机器学习的设备剩余寿命预测方法综述

基于维纳过程的退化模型，具有递归过滤算法，可用于估计剩余使用寿命

基于FPGA的奇异值和特征值分解的快速实现。

磁悬浮系统自适应模糊PID控制器的设计

最新资源

A utility-based capacity optimization framework for achieving cooperative diversity in the hierarchical converged heterogeneous wireless networks 