SIFT学习记录1

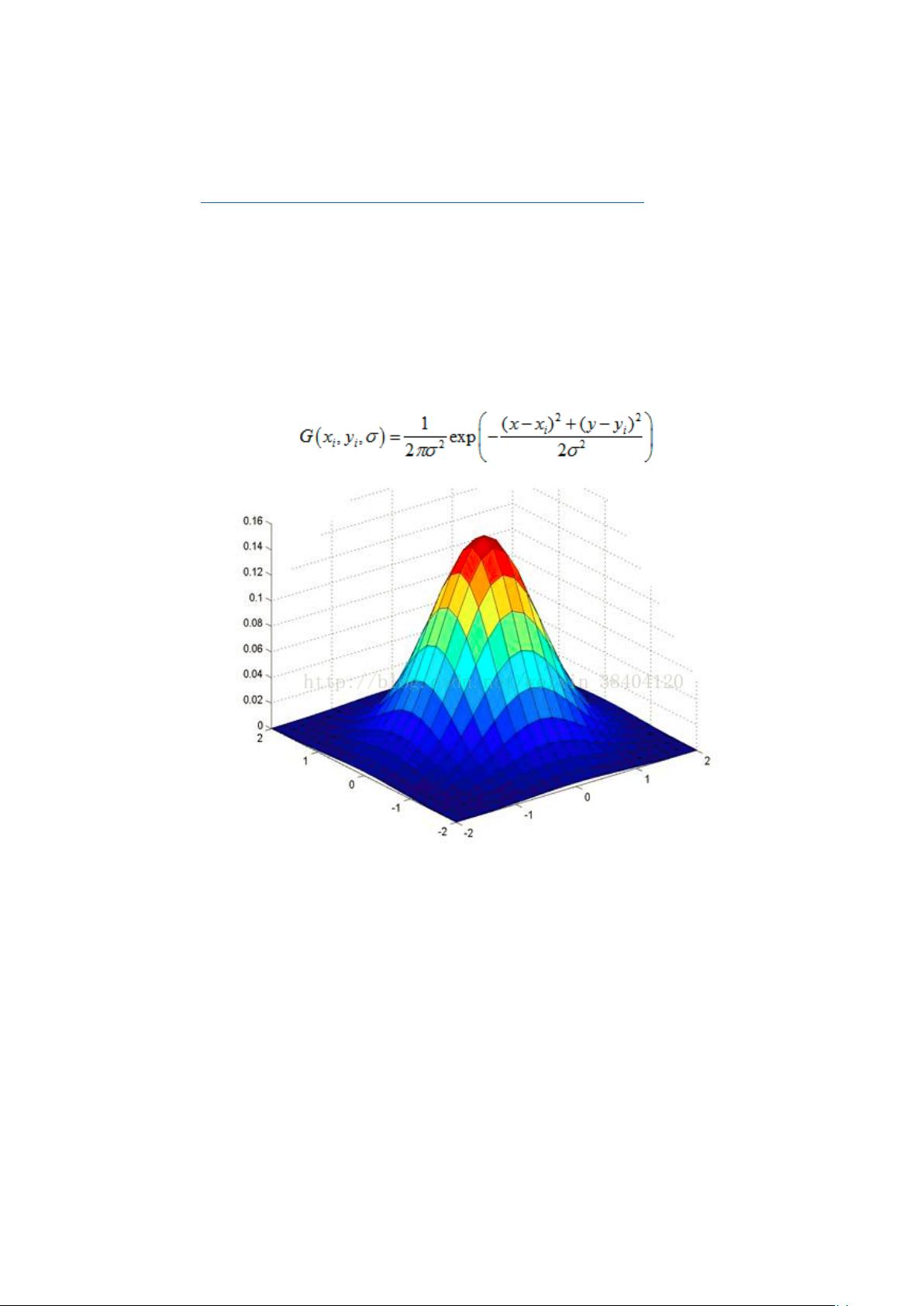
在图像处理领域，SIFT（Scale-Invariant Feature Transform，尺度不变特征变换）是一种重要的局部特征检测算法，它能够从不同尺度和旋转角度的图像中提取出稳定的特征点。本篇文章主要探讨了SIFT特征检测中的二维高斯函数及其在图像卷积中的应用。 我们需要了解的是“尺度”（Scale）的概念。在SIFT算法中，尺度通常由二维高斯函数的标准差（σ）来表示，可以理解为相对于图像的观察距离。尺度空间是通过在不同尺度下分析图像来创建的，这样可以捕捉到不同大小的物体或特征。尺度的改变意味着图像被等比例地放大或缩小，形成了一个连续的尺度层叠。 二维高斯函数在图像处理中常用于平滑或滤波操作。它是一个在x和y方向上都呈正态分布的函数，形状类似于钟形曲线。表达式一般写作： \[ G(x, y; \sigma) = \frac{1}{2\pi\sigma^2} e^{-\frac{x^2 + y^2}{2\sigma^2}} \] 其中，\( (x, y) \) 是像素坐标，\( \sigma \) 是标准差，决定了函数的宽度。高斯函数在xy方向上无限延伸，但在实际应用中，由于计算资源的限制，我们只能选取以像素为中心的一块有限大小的矩阵，通常是 \( (6\sigma+1) \times (6\sigma+1) \) 的矩阵来进行卷积，这个矩阵被称为高斯核或高斯模板。 卷积是图像处理中的基本操作，通过二维高斯函数与图像进行卷积，可以实现图像的平滑，即将相邻像素点按照高斯函数赋予的权重进行加权平均，得到新的像素值。在这个过程中，高斯函数可以看作是对每个像素点的一个概率权重，所有像素点的概率和为1。在实际计算时，由于高斯核的元素之和不等于1，因此需要对其进行归一化处理，确保卷积后的图像亮度保持不变。 在处理图像边界时，由于高斯核可能会超出图像的实际边界，导致边缘像素丢失。为解决这个问题，可以采用分离高斯模板（Separable Gaussian Kernel），即利用二维高斯函数可分解为两个一维高斯函数的性质。分离高斯模板将原来的二维核拆分为一个列向量和一个行向量，分别与图像进行一次一维卷积，这样可以减少运算量，并避免边界问题。在进行卷积时，超出图像边界的部分不参与计算，对于是否需要归一化，取决于具体的实现方式和需求。 SIFT特征检测的第一步是构建尺度空间并进行高斯滤波，二维高斯函数在这里起着关键作用。通过理解和掌握高斯函数的特性，我们可以更好地理解SIFT算法的工作原理，从而在实际应用中更有效地进行图像特征的检测和匹配。