3-3_非线性规划_无约束优化算法1

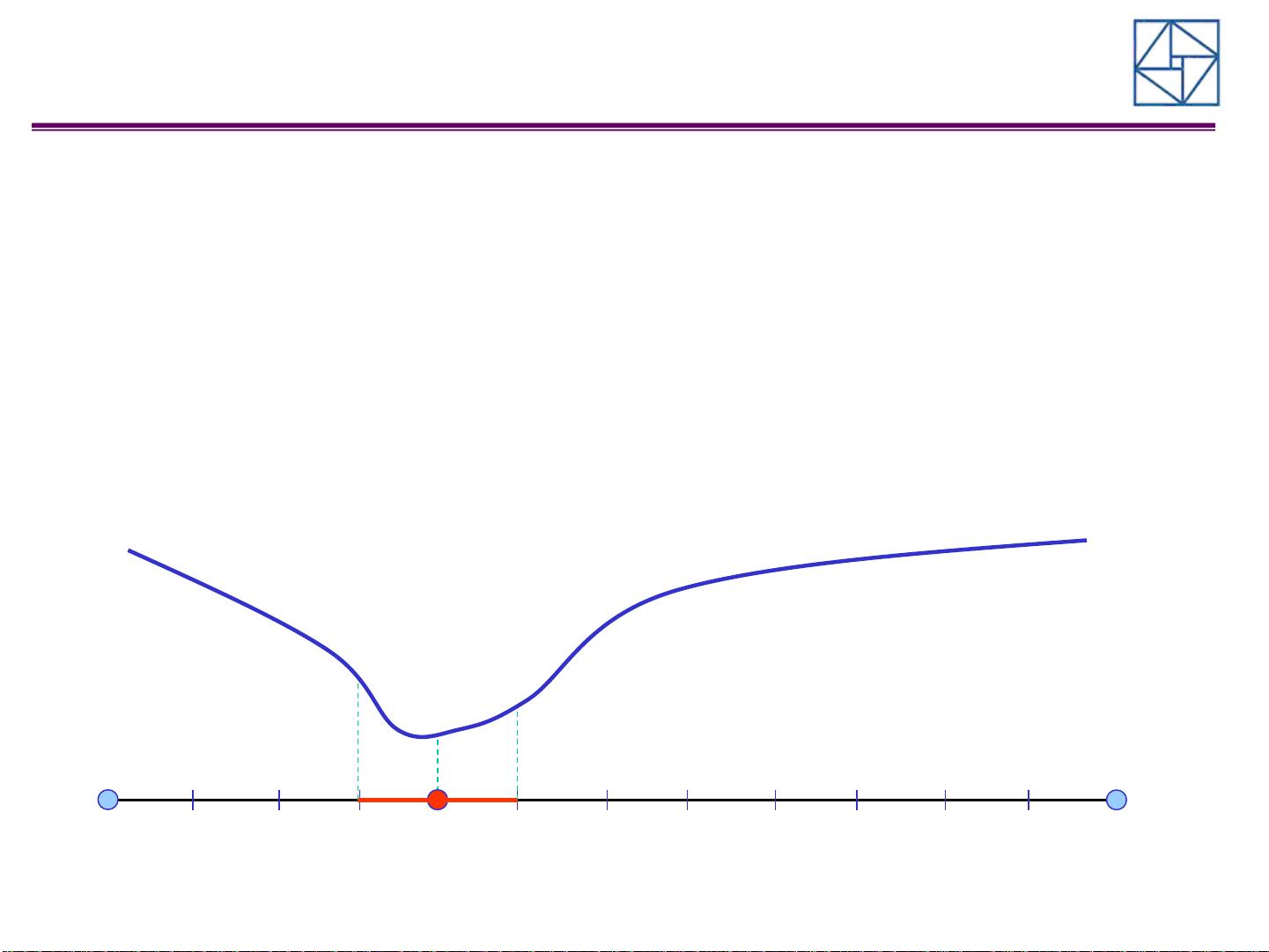
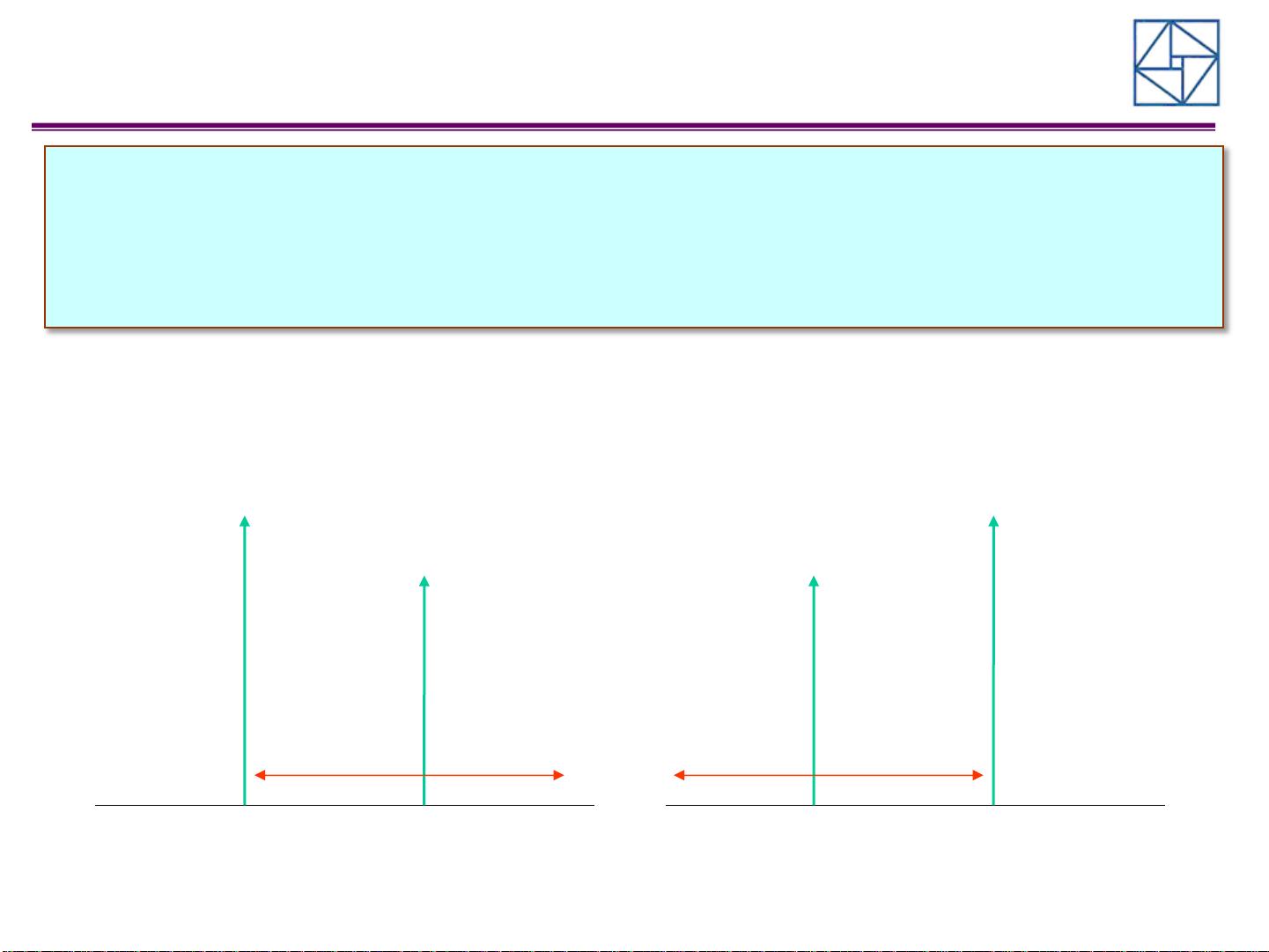
无约束优化算法是解决非线性规划问题的一种重要方法，主要关注如何在没有特定边界条件的情况下找到函数的全局最小值。线搜索是这类算法的核心部分，因为它决定了解空间中的下一个迭代点。线搜索通常涉及以下几个关键步骤： 1. **当前解**：算法开始于一个初始点 \( x_k \)，这是当前的最优解估计。 2. **终止条件**：如果 \( x_k \) 已经满足预设的终止条件（如函数值低于某个阈值或迭代次数达到上限），则输出 \( x_k \) 作为最终解，算法结束。 3. **搜索方向**：生成一个搜索方向 \( d_k \)，通常是函数梯度的负方向，用于从 \( x_k \) 向下搜索更优的解。 4. **确定步长**：选择一个合适的步长 \( \lambda_k \) 很关键。这通常涉及解决一个一维线性搜索问题，寻找使函数 \( f(x_k + \lambda_k d_k) \) 最小化的 \( \lambda \) 值。步长的选择方法有多种，例如 Armijo 条件、Wolfe 条件等，它们平衡了函数下降和搜索方向的充分下降。 5. **迭代更新**：根据选定的步长，更新解为 \( x_{k+1} = x_k + \lambda_k d_k \)，然后回到第一步，重复过程直到满足终止条件。 线搜索的方法包括一致搜索、黄金分割法、二分搜索法和斐波纳契搜索法。一致搜索预先确定多个点来评估函数值，适合函数值计算成本较低的情况。黄金分割法则更为高效，通过动态调整搜索区间，每次迭代都将区间长度缩小为原长度的 \( \alpha \) 倍，其中 \( \alpha \) 是黄金分割比例的倒数，减少了计算次数。 黄金分割法的工作流程如下： - 如果当前区间小于预设的精度 \( \epsilon \)，认为已找到近似最优解。 - 根据函数值比较选择新的边界点，并计算新的 \( \lambda \) 值。 - 通过 \( \alpha \) 更新区间，减少计算量。 - 重复上述步骤直至满足终止条件。 此外，点-集映射是一种更高级的策略，它考虑了整个解集的行为，而不只是单个点。在无约束优化中，这类方法通常涉及到更复杂的步长选择策略和动态调整搜索空间，如信赖域方法、拟牛顿法等。这些方法可能需要计算目标函数的导数或二阶信息，以提供更精确的下降方向和步长估计，从而提高算法的收敛速度和全局寻优能力。 无约束优化算法通过线搜索策略在解空间中迭代寻找最优解，不同类型的线搜索方法在效率和复杂性之间取得平衡，适应不同的问题特性和计算资源。在实际应用中，选择合适的线搜索策略和优化算法对于解决问题至关重要。