如何平均得到圆内点的随机分布1

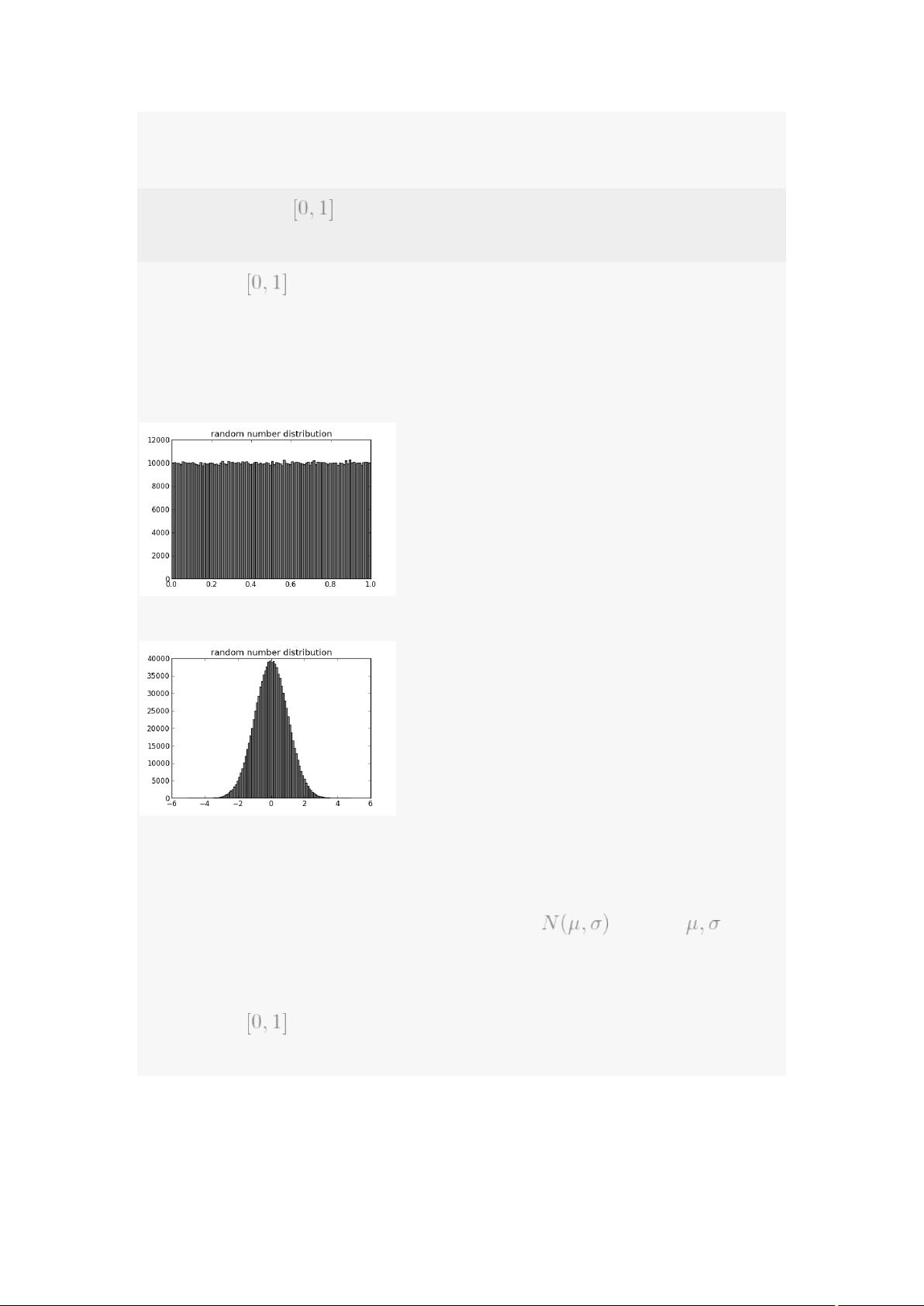
在IT领域，尤其是在算法设计和数据分析中，均匀随机分布是一个重要的概念。本文主要探讨如何在单位圆内生成平均分布的随机点，确保点在圆的面积上均匀分布。以下是几个关键知识点： 1. **平均随机分布**：平均随机分布意味着在指定区间内，每个子区间的元素出现的概率是相等的。例如，对于一个区间[0, 1]，如果随机生成一个数，每个小段[0, 0.1), [0.1, 0.2), ..., [0.9, 1)内生成的点数量应该是大致相等的。 2. **正态随机分布**：正态分布，也称为高斯分布，以钟形曲线表示，具有均值μ和标准差σ。在正态分布中，数据集中在均值附近，随着距离均值增加，数据的出现概率逐渐减小。 3. **生成单位圆内的随机点**：目标是在单位圆内生成随机点，使得它们在圆的面积上均匀分布。这是因为在几何上，面积的均匀分布意味着点在任何区域内的概率与其面积成比例。 4. **算法分析**： - **算法1**：从一个大正方形中随机选取点，如果点在圆内，则返回。虽然简单，但效率较低，因为大部分点可能在圆外，需要多次尝试。 - **算法2**：基于x和y坐标分别在[0, 1]范围内随机分布，然后通过转换生成圆上的点。但这种方法导致靠近圆心的点过于密集，不满足均匀分布要求。 - **算法3**：采用极坐标系统，随机生成角度和半径，其中半径在[0, 1]范围内。然而，这种方法同样导致靠近圆心的点过多。 - **算法4（正解）**：同样使用极坐标，但随机生成半径的平方，这样可以确保点在圆上的分布更均匀，因为较小的半径平方对应较大的面积。 5. **算法4的改进**：算法4的关键在于生成半径的平方，而不是半径本身。这样可以使得点在远离圆心的地方更稀疏，在靠近圆心的地方更密集，从而在整体上实现面积上的均匀分布。 6. **概率分析**：在算法1中，连续3次取不到圆上点的概率为(1-r^2)^3，其中r是圆的半径（这里是1）。3次尝试取到圆上点的概率至少为1-(1-r^2)^3，对于单位圆，这个概率接近75%，保证了较高效率。 7. **概率密度函数**：在统计学中，概率密度函数（PDF）描述了一个随机变量的概率分布。在正态分布中，PDF是一个关于均值对称的钟形曲线。对于单位圆内的随机点生成，理想的PDF应是常数，这意味着在圆的任何位置生成点的概率相同。 通过上述算法分析和概率理解，我们可以设计出在单位圆内生成均匀分布随机点的有效方法。在实际应用中，这种技术可能用于模拟、统计分析、图形渲染等领域，确保结果的随机性和公正性。