模式识别实验3PCA1

【模式识别实验3PCA1】主要探讨了使用PCA（主成分分析）进行数据降维和特征提取的方法。PCA是一种在统计学和机器学习领域广泛应用的技术，它的目标是找到原始高维数据的新坐标系，使数据在新坐标系下的投影最大化方差，从而减少数据的复杂性，同时保留大部分信息。 实验的目的是通过MATLAB实现PCA，理解和掌握PCA的基本原理。PCA的核心在于寻找数据集的主成分，即那些能够最大程度解释数据方差的方向。这些主成分是原数据的线性组合，按照它们所解释的方差大小排序。通过将数据映射到由主成分构成的空间，可以有效地降低数据的维度，同时保持数据集中的大部分变异信息。 PCA的过程包括以下几个步骤： 1. **数据预处理**：通常需要对数据进行中心化处理，即将数据减去均值，使得数据集的均值为零。 2. **计算协方差矩阵**：对于中心化后的数据，计算其协方差矩阵，该矩阵反映了各个特征之间的相互关联程度。 3. **特征值分解**：对协方差矩阵进行特征值分解，得到一组特征向量和对应的特征值。特征值表示对应特征向量方向上的数据方差。 4. **选择主成分**：按特征值的大小对特征向量排序，选择前k个具有最大特征值的特征向量作为主成分，其中k是希望降维到的维度。 5. **投影数据**：将原始数据投影到由这k个主成分构成的新空间中，完成降维过程。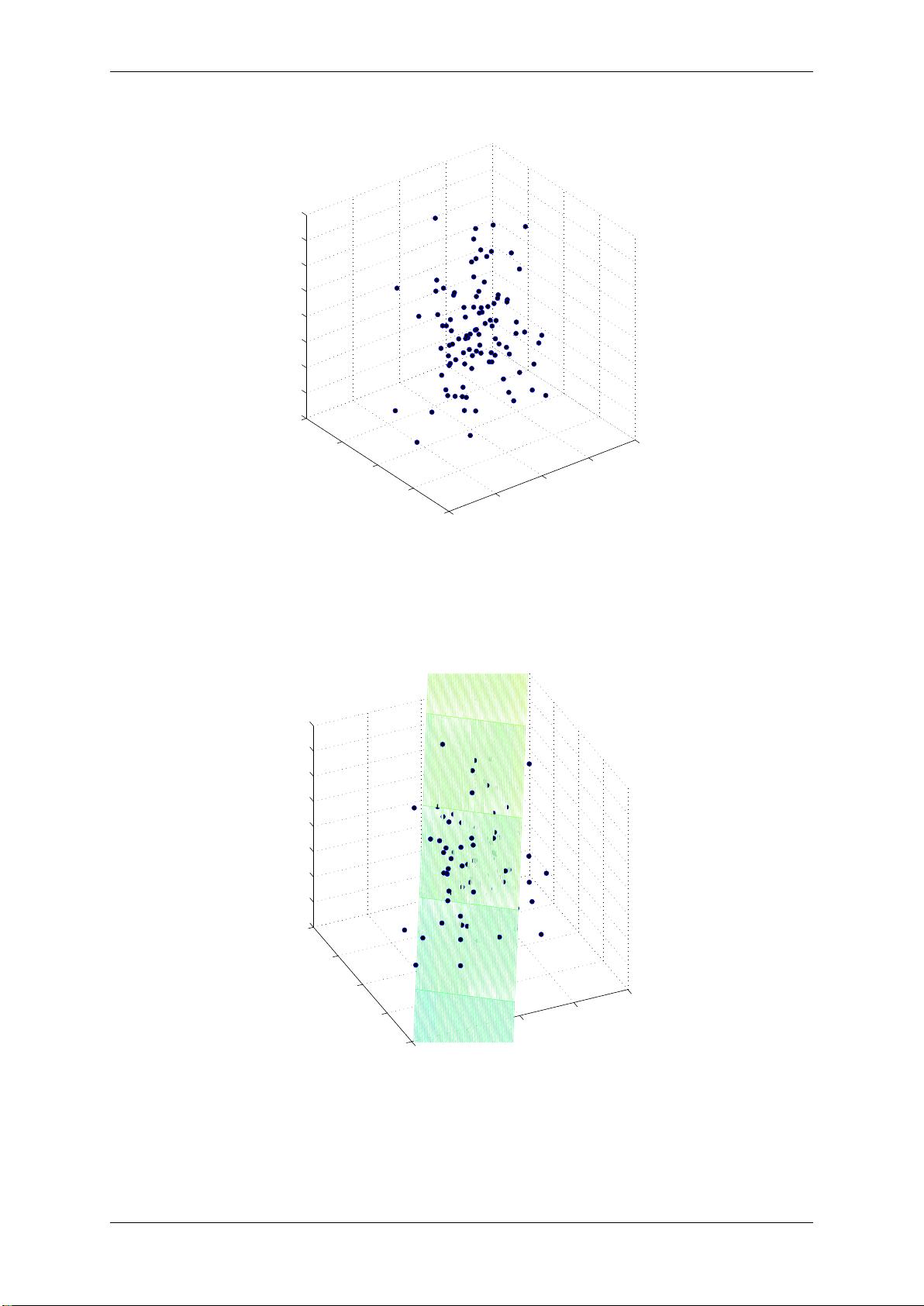 实验内容包括对不同数据集的PCA应用，例如2D或3D数据的可视化，展示降维前后的变化。实验结果可能包含多个图示，如散点图，展示了数据在主成分轴上的分布，帮助理解降维的效果。 通过实验，我们可以观察到PCA如何减少数据的复杂性，同时观察到降维后数据的主要趋势和结构。实验还可能涉及计算和比较降维前后的信息损失，以及验证PCA在保持数据重要特性的同时，如何简化数据表示。 实验心得体会强调了PCA在实际问题中的价值，例如在高维数据的可视化、特征选择和模型简化等方面的应用。此外，还可能提到了PCA的局限性，如对异常值敏感，以及在某些情况下可能无法捕获非线性关系。 总结来说，模式识别实验3PCA1是一次深入理解PCA理论并实践其应用的过程，通过这个实验，学生可以更好地掌握PCA的基本思想，提升数据分析和处理的能力。