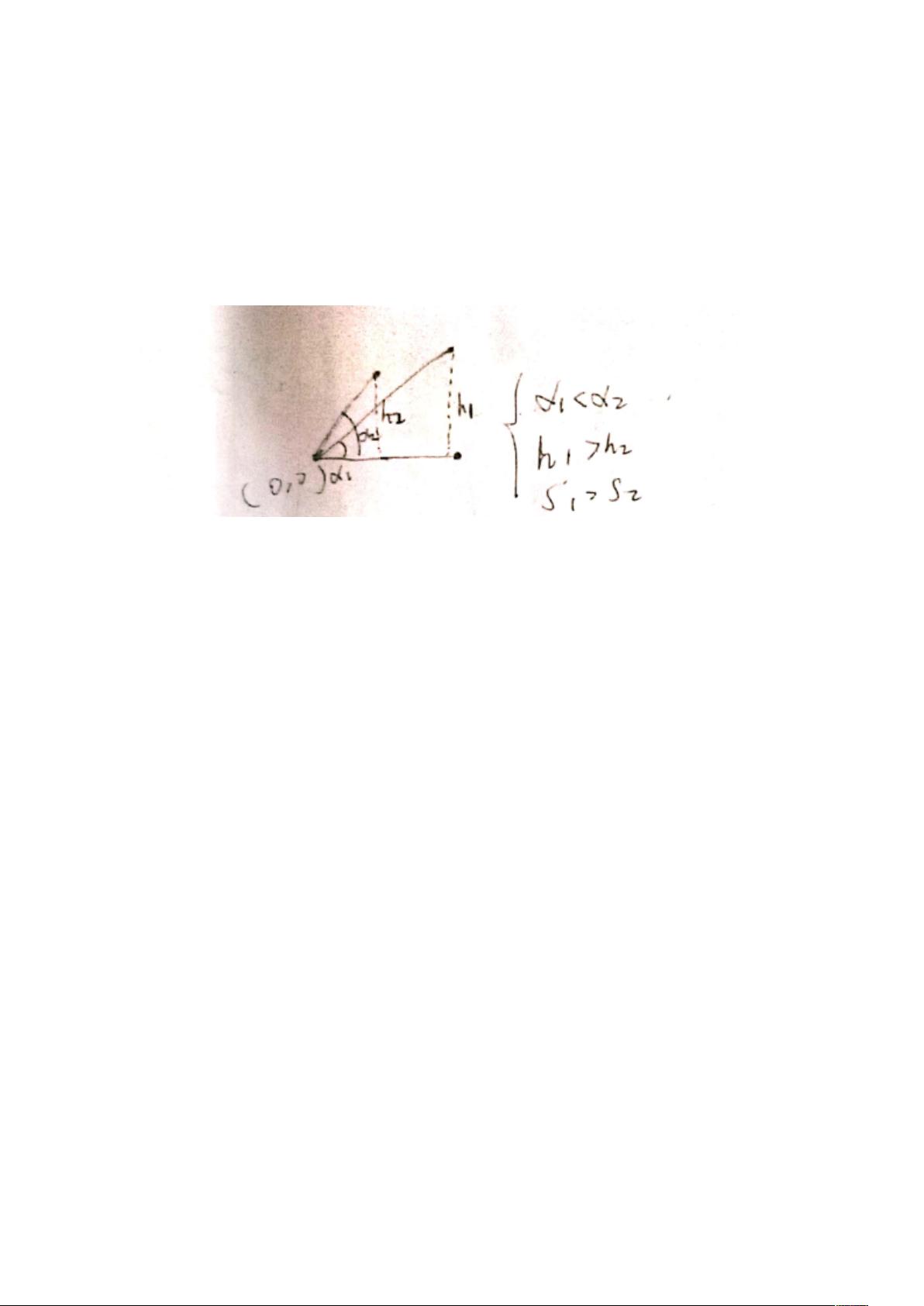L3021 神坛 的一些错误做法(目前网上的方法没一个是对的) 和 一些想法1

标题 "L3021 神坛 的一些错误做法(目前网上的方法没一个是对的) 和 一些想法1" 涉及的问题主要集中在计算几何中的最小三角形问题，特别是利用极角排序来寻找最小三角形的一种常见误解。描述中提到的错误做法是试图通过极角排序和判断向量之间的关系来确定最小三角形的边。 错误做法详解： 在计算几何中，极角排序是一种常用的优化策略，通常用于解决与点集相关的几何问题。对于给定点集，极角排序是将点按照相对于固定点（通常是原点）的极角进行排序。然而，在寻找最小三角形的情况下，错误在于简单地将点按照向量叉积大小排序。向量AB(x1, y1)和AC(x2, y2)的叉积可以用来计算它们围成的三角形面积，即|y2*x1 - y1*x2|。极角排序是根据y2*x1 > y1*x2将点B排在点A之后，但这并不保证能形成最小的三角形。 问题在于，这种排序不能确保最小三角形的两边是极角相邻的。例如，描述中给出的样例展示了当输入为(60, -2), (-1, 0), (0, 1), (0, 0), (50, -50), (-50, -50)时，按照错误方法得到的输出是26.000，而正确的输出应该是2.000。这是因为极角排序不能正确反映边的相对重要性，特别是在处理那些能够形成更小三角形的角度组合时。 一些想法与解决方案： 1. 边的作用范围：可以通过限制某些边的作用范围，使得另一条边在特定角度范围内被选中。这种方法虽然可以降低某些情况的影响，但时间复杂度仍然较高。 2. 单调队列：考虑使用单调队列来优化算法，但实现起来有困难。单调队列通常用于维护有序序列，当新元素插入或旧元素移除时，队列保持单调递增或递减。然而，在这个场景中，由于边的作用域不仅由相邻边决定，而且不具有连续的顺序，因此应用单调队列比较复杂。 3. 确定旋转方向：设想确定一个旋转方向，使得前面的边只在角度较大时才对结果产生影响。这种方法的问题在于，它不能精确地确定一条边的作用域，因为这不仅取决于相邻边，还可能受到其他非相邻边的影响。 寻找最小三角形的正确方法需要更精细的几何分析和数据结构设计。极角排序虽然在某些情况下有用，但在本问题中不能直接解决问题。需要探索其他方法，如动态规划、线段树、堆等数据结构，或者结合特定的几何性质来优化算法。在实际编程中，应谨慎对待网上找到的解法，并确保理解其背后的数学原理，以便正确地解决此类问题。