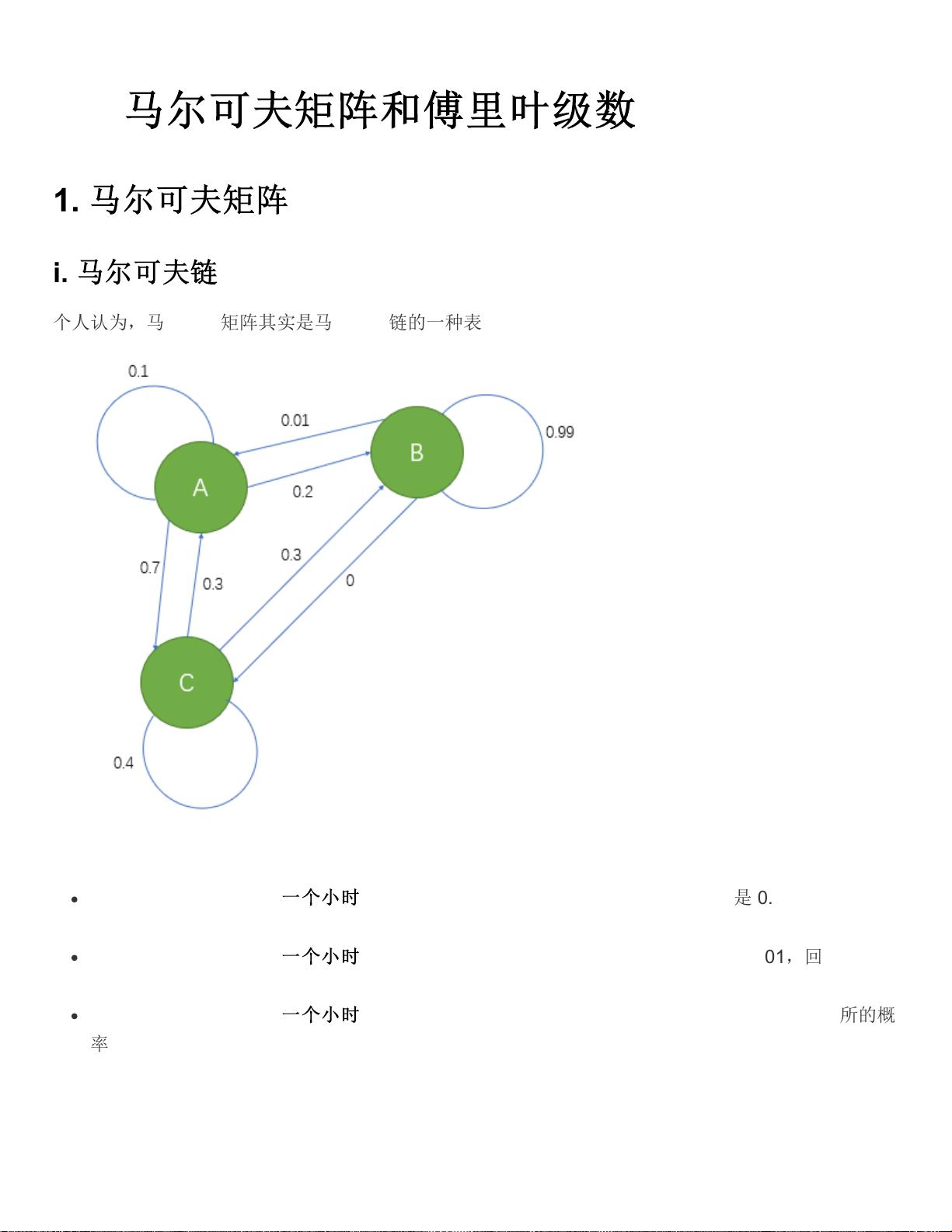
马尔可夫矩阵是概率论中的一个重要概念,它在描述离散时间随机过程的状态转移时起着关键作用。马尔可夫链,也就是基于马尔可夫矩阵的模型,假设系统未来的状态只依赖于当前状态,而不依赖于它是如何到达当前状态的。这被称为“无记忆”或“马尔可夫”性质。 例如,假设我们有三个房间——厨房、厕所和卧室,形成了一个简单的马尔可夫模型。每个房间代表一个状态,模型描述了从一个房间转移到另一个房间的概率。比如,如果我们在厨房,那么一个小时后仍然留在厨房的概率是0.1,去厕所的概率是0.2,去卧室的概率是0.7。同样,如果我们当前在厕所,一个小时后仍在厕所的概率是0.99,去厨房的概率是0.01,去卧室的概率是0。卧室的情况是,一个小时后仍在卧室的概率是0.4,去厨房的概率是0.3,去厕所的概率是0.3。 马尔可夫矩阵是一个方阵,其中的元素代表从一个状态转移到另一个状态的概率。对于上述三个房间的例子,马尔可夫矩阵如下: \[ A = \begin{bmatrix} 0.1 & 0.2 & 0.7 \\ 0.01 & 0.99 & 0 \\ 0.3 & 0.3 & 0.4 \end{bmatrix} \] 马尔可夫矩阵有一些重要的性质:所有元素非负,且每一行的和为1,保证了概率的合理性。此外,马尔可夫矩阵的幂仍然是马尔可夫矩阵,这是因为概率的乘积仍为概率。 马尔可夫矩阵的稳态是指当时间无限大时,系统达到的一种平衡状态,即无论初始状态如何,系统的长期行为将稳定在一组特定的概率分布上。这个平衡状态可以通过寻找矩阵的特征值和特征向量来确定。特别是,如果矩阵有一个特征值为1,那么对应的特征向量就表示稳态分布,因为当时间趋向无穷大时,马尔可夫矩阵的幂会趋向于这个特征向量。 对于任何马尔可夫矩阵,总是存在一个特征值为1,这是因为矩阵的每一列和为1,减去单位矩阵后的矩阵的行列式为0,这意味着至少有一个特征值为1。其他特征值的绝对值小于1,表示系统最终会收敛到稳态分布。 马尔可夫矩阵在各种实际问题中有着广泛的应用,如人口迁徙、语言模型、网络流量分析等。例如,教授提到人口迁徙的例子,假设加州和麻省的人口可以用一个二维向量表示,状态转移方阵描述了人口从一个州迁移到另一个州的概率。通过计算矩阵的幂,我们可以预测未来任意时间点两个州的人口比例。 马尔可夫矩阵提供了一种强有力的工具,用于建模和分析具有马尔可夫性质的随机过程,它在理解动态系统的行为以及进行长期预测方面具有重要价值。
- 粉丝: 26
- 资源: 320
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功
评论0