02-D2-4 原理 & 02-D2-5 实现 & 02-D2-6 实例1
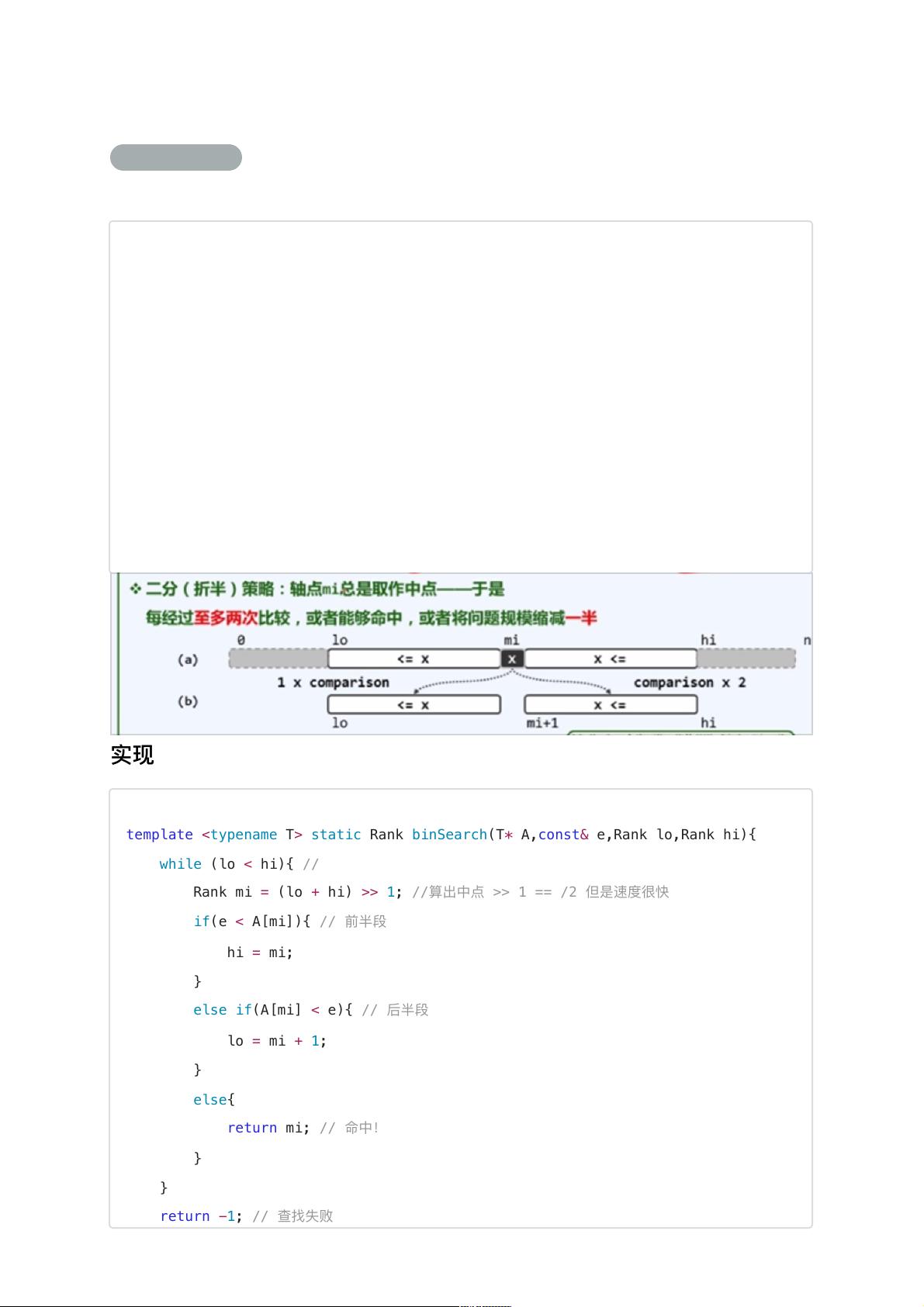
在数据结构领域,二分查找(Binary Search)是一种高效的算法,尤其适用于有序数组或列表的查找操作。这个算法的核心思想是通过不断将查找区间减半来快速定位目标元素。02-D2-4 原理、02-D2-5 实现以及02-D2-6 实例主要讲解了如何运用二分查找来解决查找问题。 **二分查找原理**: 二分查找算法基于分治策略。假设我们有一个已排序的数组S,我们要查找的目标元素为e。我们可以取数组中间的元素x = S[mi]作为参照。根据比较结果,我们可以将数组分为三个部分: 1. S[lo, mi):这部分的所有元素都小于或等于x。 2. S(mi, hi):这部分的所有元素都大于x。 3. S[mi]:元素x本身。 如果e等于x,那么我们直接返回mi,查找结束;如果e小于x,我们只需在前半部分S[lo, mi)中继续查找;如果e大于x,我们在后半部分S(mi, hi)中查找。每次比较都能将查找区间缩小至少一半,直到找到目标元素或查找区间为空。 **二分查找实现**: 上述描述的二分查找算法可以用C++模板函数来实现,代码如下: ```cpp template <typename T> static Rank binSearch(T* A, const T& e, Rank lo, Rank hi) { while (lo < hi) { Rank mi = (lo + hi) >> 1; // 计算中间索引,位移操作比除法更快 if (e < A[mi]) { // 如果e小于中间元素,查找左半部分 hi = mi; } else if (A[mi] < e) { // 如果中间元素小于e,查找右半部分 lo = mi + 1; } else { return mi; // 找到目标元素,返回索引 } } return -1; // 查找失败,返回-1 } ``` 这个函数首先检查lo是否小于hi,如果满足条件,说明还有待查找的区间。计算中间索引mi,然后根据比较结果更新查找区间。每次循环都将查找范围缩小至原来的一半,直到找到目标元素或者查找区间为空。 **二分查找实例分析**: 对于实例S.search(8, 0, 7),我们假设数组S为[1, 3, 5, 7, 9]。目标值e为8,初始查找范围为0到7。按照二分查找步骤,我们将不断缩小查找区间: 1. 查找中点,mi=3,比较8与S[3]=5,8大于5,所以在后半部分[4, 7]查找。 2. 新的mi=5,比较8与S[5]=9,8小于9,所以在前半部分[4, 4]查找。 3. 此时mi=4,比较8与S[4]=7,8大于7,所以在后半部分[4, 4]查找,但此时区间为空,表示查找失败。 递归跟踪显示,每次都是取出中间元素并根据比较结果调整查找区间,递归深度为O(logn),每个递归实例的时间复杂度为O(1)。因此,整个算法的时间复杂度为O(logn),远优于线性查找的O(n)。 总结来说,二分查找算法通过分治策略高效地在有序数组中查找目标元素,其效率与数据量呈对数关系,非常适合大数据量场景。在实现过程中,注意选取中间元素并正确更新查找区间,是确保算法正确性的关键。
- 粉丝: 37
- 资源: 351
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功
评论0