3-6_逆矩阵及矩阵可逆条件1
需积分: 0 80 浏览量
更新于2022-08-04
收藏 573KB PDF 举报
逆矩阵是线性代数中极为关键的概念之一,它在解决线性方程组、矩阵理论以及其他相关数学领域中具有不可替代的作用。在本节内容中,我们将深入探讨逆矩阵的定义、性质以及矩阵可逆的条件。
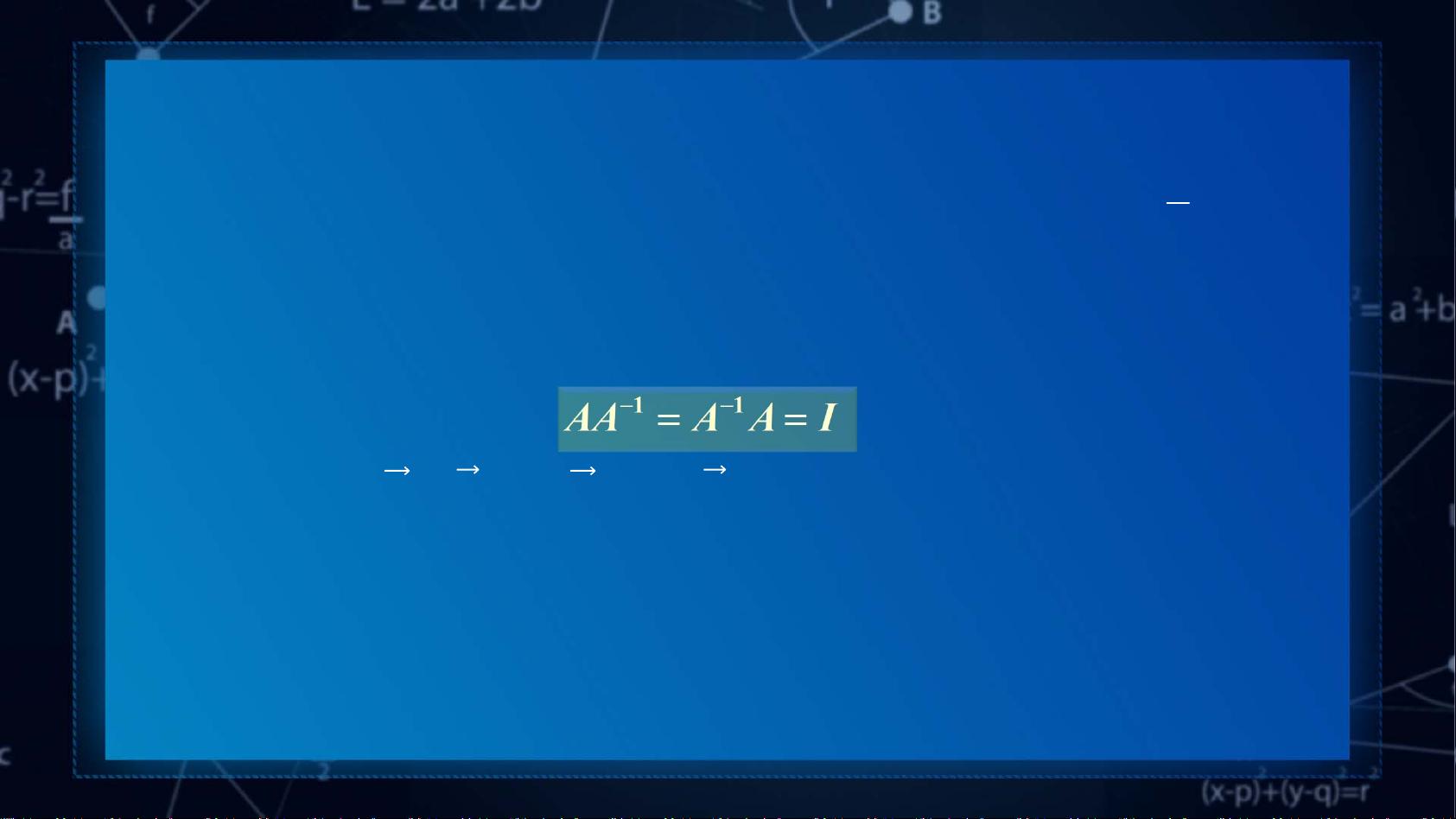
让我们从逆矩阵的定义开始。逆矩阵实质上是与某个方阵相乘后能得到单位矩阵的一个矩阵。具体来说,假设有矩阵A,我们希望找到另一个矩阵B,使得它们的乘积满足AB=BA=In,其中In为n阶单位矩阵。满足这一条件的矩阵B即是矩阵A的逆矩阵,记作A^-1。这里,A必须是一个方阵,因为只有方阵才能保证乘积能够得到一个单位矩阵。
矩阵可逆的条件包括两个主要方面。一是矩阵必须是方阵,这确保了乘积有可能得到单位矩阵;二是矩阵不能是奇异的,即其行列式不能为零。这一点至关重要,因为一个矩阵的行列式为零,意味着它没有逆矩阵。因此,可逆矩阵的行列式必然是非零值。
在讨论了逆矩阵的定义和可逆条件之后,我们来进一步探讨逆矩阵的一些基本性质。这些性质在理解和操作逆矩阵时具有指导性的意义。
第一,逆矩阵的逆仍然是原矩阵本身,即(A^-1)^-1=A。这说明逆矩阵的逆运算仍然是可逆的,具有互逆的特性。
第二,矩阵乘积的逆遵循逆运算的乘法规则,即(AB)^-1=B^-1A^-1。这一性质表明,如果将两个可逆矩阵相乘,它们乘积的逆是各自逆矩阵的反向乘积。
第三,若对矩阵进行数乘,其逆矩阵则是数的倒数乘以原矩阵的逆,即(kA)^-1=k^-1A^-1。这一性质在处理数乘变换时非常有用。
第四,矩阵转置的逆等于逆矩阵的转置,即(AT)^-1=(A^-1)^T。此性质强调了逆矩阵与原矩阵转置的关系,这在几何变换和对称性的探讨中十分关键。
除上述性质外,初等矩阵总是可逆的,并且它们的逆矩阵可通过执行相反的初等变换获得。对于二阶矩阵,其可逆性可由一个简单的计算来确认,并且可以直接写出它的逆矩阵。
虽然逆矩阵有诸多性质和计算方法,但并非所有矩阵都有逆矩阵。例如,奇异矩阵和非方阵均没有逆矩阵。在实际问题中,我们通常借助矩阵的行列式来判断一个矩阵是否可逆。如果一个方阵的行列式为零,那么它不可逆。Cramer法则是一种基于逆矩阵计算解的方法,它适用于行列式非零的线性方程组,但若矩阵不可逆,则此法不适用。
总结而言,逆矩阵为线性方程组的求解提供了强大的工具。它是线性代数中用于分析和解决线性系统的关键概念。通过掌握逆矩阵的定义、性质和计算方法,我们能够更深入地理解线性系统的本质,并在科学、工程以及经济学等领域中应用这些理论来处理实际问题。因此,学习和掌握逆矩阵的相关知识对于任何涉及到数学应用的领域都是至关重要的。
余青葭
- 粉丝: 44
- 资源: 303
最新资源
- c语言实现水波纹显示效果.zip
- c语言实现图片转化为 ASCII 图.zip
- “面食文化”:中国传统面食网站设计与用户体验优化
- 基于C#的库存管理系统
- 基于分时电价,采用改进粒子群算法 参考lunwen:基于V2G的电动汽车充放电优化调度策略 有注释简单易懂,可自己调整参数
- c语言贪吃蛇游戏的双人对战版.zip
- 机械设计六角批头自动供料分料机(sw18可编辑+工程图+BOM)全套设计资料100%好用.zip
- django项目实战之旅游推荐数据分析可视化(源码+部署说明).zip
- c语言坦克游戏源代码.zip
- c语言通讯录管理系统源码.zip
- c语言图书管理系统源码.zip
- c语言图书借阅系统源码.zip
- MMC-HVDC仿真模型,pscad柔性直流输电仿真mmc仿真模型,双端mmc模型,MMC为21电平NLM和均压控制,还有多端如张北直流电网以及基本mmc逆变器,自己为biye网上收集的一些觉得有用的
- c语言涂格子游戏源码.zip
- c语言万年历源码.zip
- 禹霖科技原铱塔智联iot-iita物联网平台,包含了品类、物模型、消息转换、插件管理、设备管理、设备分组、规则引擎、第三方平台接入、数据流转、数据可视化、告警中心等模块,支持es/td等多种时序数据库