林轩田《机器学习基石》课程笔记4 -- Feasibility of Learning1

《机器学习基石》课程笔记4探讨了机器学习的可行性，主要围绕三个主题展开：学习的不可能性、概率的救援以及与学习的关联。它指出机器学习在面对某些问题时可能无法找到一个通用的解决方案，这是因为不同的模型可能在训练数据上表现良好，但在未见过的数据上却无法保持准确性。这一现象被称为“没有免费午餐”(No Free Lunch, NFL)定理，意味着不存在一种学习算法总能在所有问题上优于其他算法。 接着，笔记引入概率论的概念，以解决机器学习中的不确定性。通过概率理论，我们可以利用有限的样本数据对整体的未知情况进行推断。例如，通过随机抽取样本估计罐子中橙色球的比例，即使不能确定确切比例，但随着样本数量增加，我们可以得到一个大概且接近真实比例的估计，这就是Hoeffding不等式的基础。在机器学习中，这相当于通过大量独立同分布的训练样本来估计模型在所有数据上的表现，即Probably Approximately Correct (PAC)学习框架。 PAC学习理论提供了一种度量模型在未知数据上的泛化能力的方法。它将模型在训练数据上的错误率（）与在所有数据上的错误率（）联系起来。如果在训练数据上的错误率很低，那么在所有数据上的错误率也很可能很低。Hoeffding不等式确保了这种概率关系，允许我们在有限的样本上构建模型，同时有信心它在更大的数据集上也能表现良好。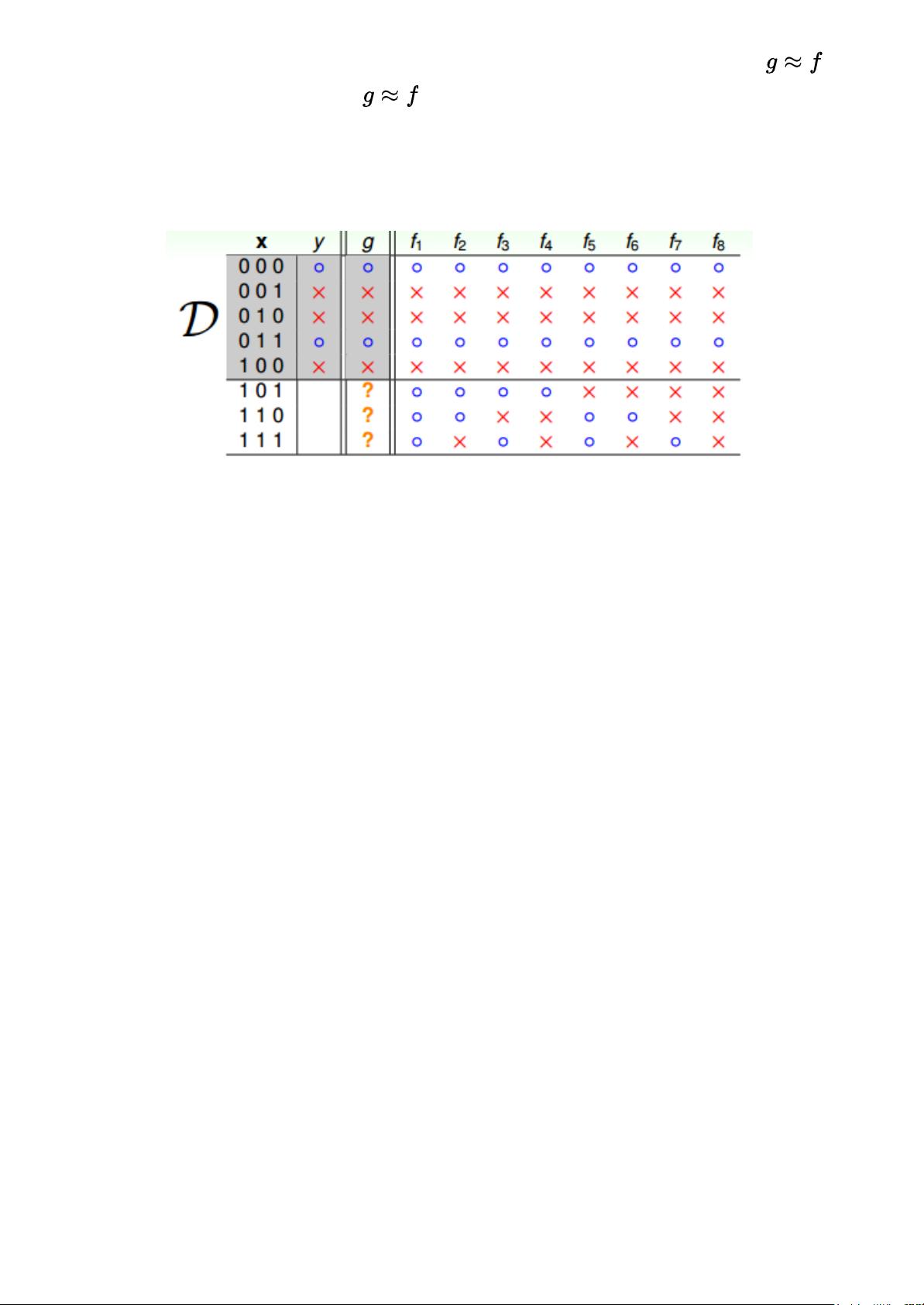 在机器学习的上下文中，假设（hypothesis）与目标函数（target function）的匹配程度可以通过概率来量化。如果训练样本足够大且独立同分布，那么我们可以通过训练样本的错误率来近似整个数据分布的错误率。这使得机器学习模型能够在采样数据之外的全局数据上进行有效的预测。 总结而言，笔记4讨论了机器学习的局限性，揭示了学习过程中必须考虑的不确定性和泛化能力。通过概率理论和PAC学习，我们可以理解如何从有限的训练数据中构建模型，并期望这些模型能够在未见过的数据上表现出良好的性能。然而，这也依赖于一些关键条件，如样本的独立同分布和足够的样本数量。因此，在实际应用中，选择合适的学习算法、保证数据质量以及正确评估模型的泛化能力至关重要。