机器学习 吴恩达 课堂笔记1

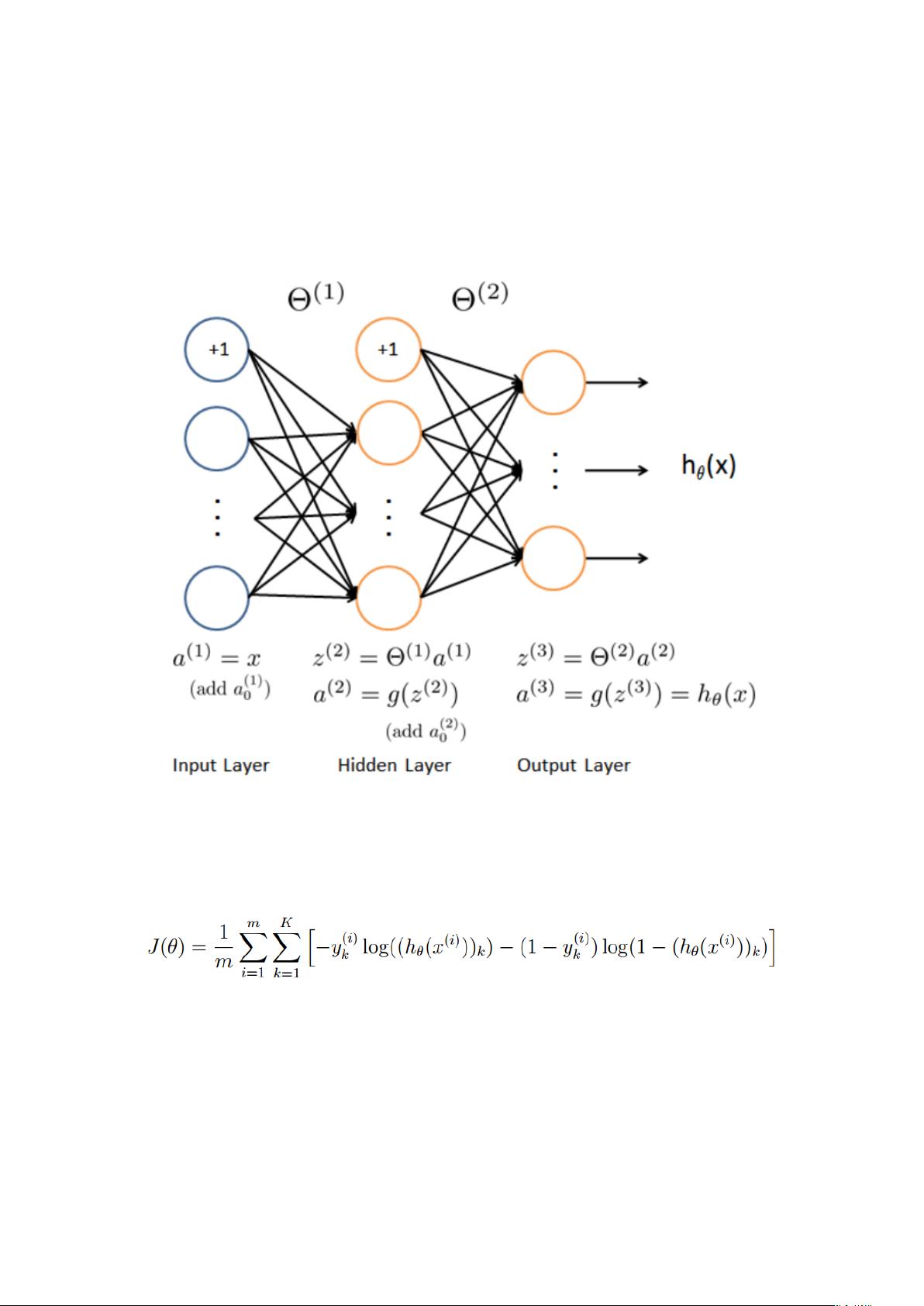
《机器学习基础与实践》 在机器学习领域，吴恩达的课程被广泛视为入门的经典。本篇笔记主要涵盖了线性回归、逻辑回归以及神经网络的基础知识，同时也讨论了模型优化和评估的方法。 1. 线性回归： 线性回归是一种基本的预测模型，其假设函数采用线性形式。在矩阵表示中，假设函数为θTX，其中θ是参数向量，X是特征向量。成本函数（Cost Function）J(θ)定义为所有数据点误差的平方和，m表示样本数量。为了找到最小化成本的θ，我们使用梯度下降法，迭代公式为θ_j := θ_j - α(1/m)∑(h_θ(x_i) - y_i)x_ij，其中α是学习率，控制下降步幅。 2. 逻辑回归： 逻辑回归在处理分类问题时，通过引入非线性的sigmoid函数进行转换。假设函数为g(θTX)，其中g是sigmoid函数。其成本函数与线性回归类似，但使用交叉熵作为损失函数。同样利用梯度下降法求解最优θ，梯度迭代公式与线性回归相同。 3. 正则化： 正则化用于防止过拟合，通过添加惩罚项限制模型复杂度。在线性回归中，正则化后的成本函数为J(θ) = (1/(2m))∑(h_θ(x_i) - y_i)^2 + (λ/2m)∑θ_j^2，λ是正则化参数。逻辑回归中正则化项同样作用于θ，但通常忽略θ_0。 4. 神经网络： 神经网络由多个逻辑回归单元组成，形成多层结构。其成本函数考虑所有输出节点的损失，对于K类分类问题，有m个样本，L层网络，sl是第l层神经元数，成本函数更为复杂。反向传播算法用于计算梯度，实现权重更新。 5. 模型优化与选择： 优化策略包括获取更多数据、特征选择、特征工程（如多项式特征）、调整正则化参数λ。训练集、交叉验证集和测试集的划分有助于评估模型的泛化能力。高偏差（欠拟合）模型需要增加模型复杂度，而高方差（过拟合）模型则需正则化或增加数据。 6. 学习曲线与模型性能： 学习曲线展示了训练集大小对训练误差和验证误差的影响。高偏差时，两者都高，而高方差时，训练误差低，验证误差高。增加正则化λ能缓解过拟合，减少λ可减轻欠拟合。 7. 评估指标： 对于分类任务，查准率（Precision）关注预测为正例中的真正例比例，召回率（Recall）关注所有真正例被正确识别的比例。准确率（Accuracy）是最常见的评估指标，但在类别不平衡时可能不准确。 机器学习涉及模型构建、优化、评估等多个环节，需要综合运用各种技巧和理论来提升模型性能。理解并掌握这些基本概念，是通往深度学习和更高级机器学习技术的关键。