D11_2对坐标曲线积分1

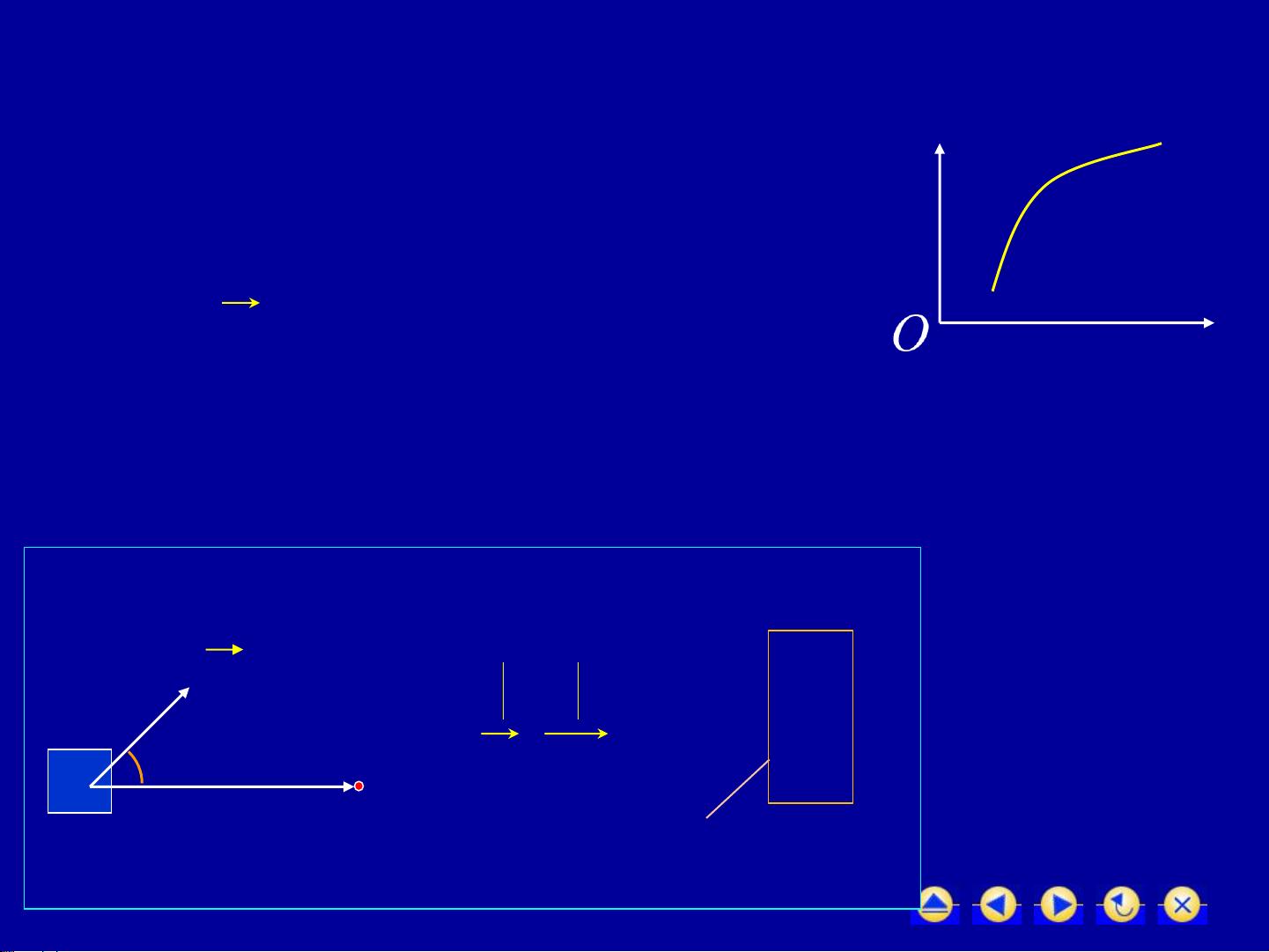
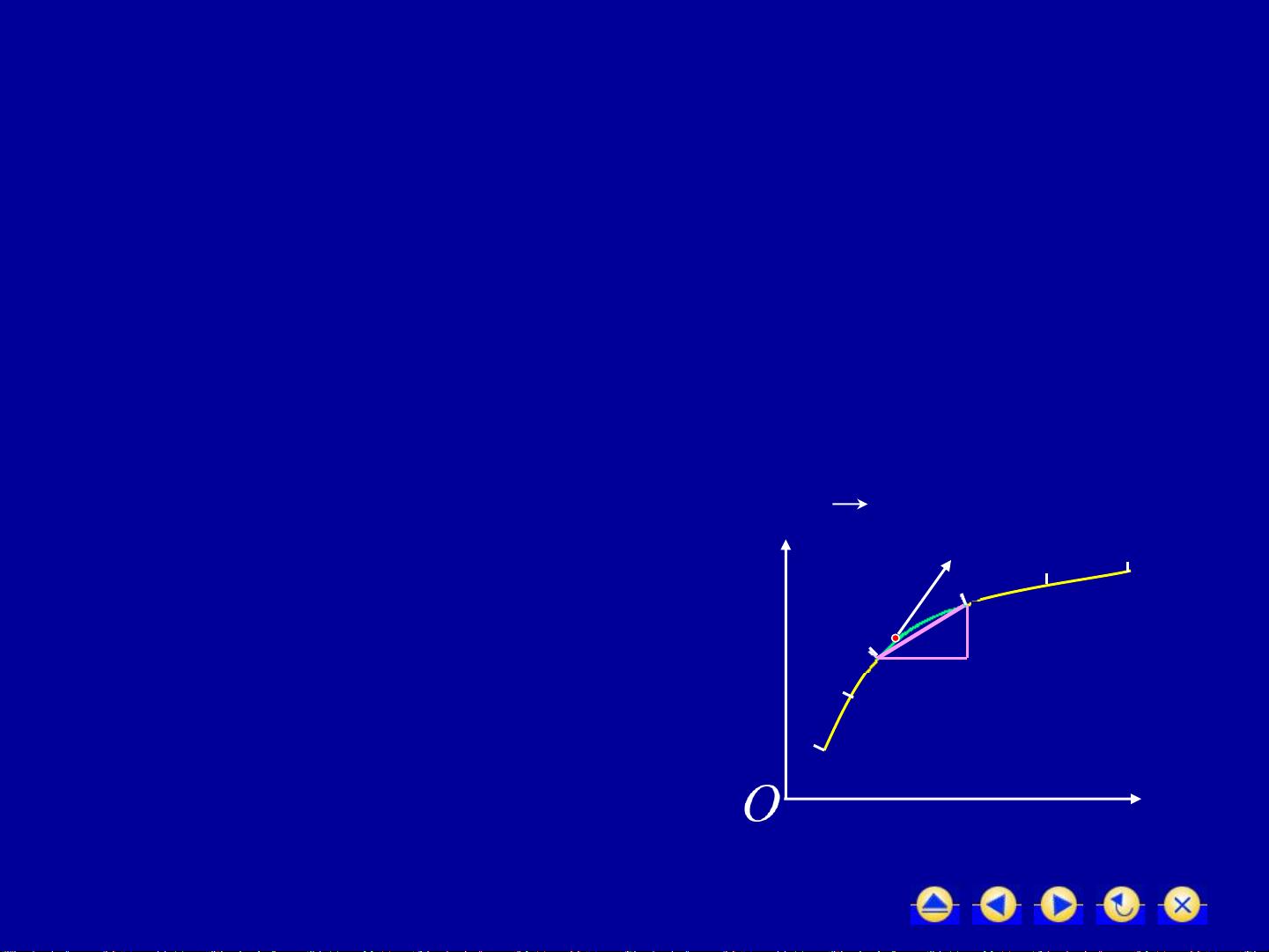
在数学的微积分学中，对坐标的曲线积分是一种积分形式，主要用来计算在曲线上某函数的累积效果，例如力在物体沿着曲线移动时所做的功。本知识点主要围绕平面内的对坐标的曲线积分展开，包括其概念、计算方法以及性质。 对坐标的曲线积分的概念通常涉及到变力沿曲线做功的问题。例如，当一个质点在xOy平面上受到一个大小和方向都可能变化的力的作用，从点A沿着光滑曲线L移动到点B，我们需要计算这个变力在整个过程中所做的功。如果力是恒定的，我们可以直接用直线上的定积分来计算；但对于变力，我们通过"大化小"、"常代变"、"近似和"、"取极限"这四个步骤，将曲线L分割成多个小弧段，然后利用微元法，将每个小弧段上的功近似表示为该段上的平均力乘以弧段长度，最后将所有小段的功求和并取极限，得到整个曲线上的总功。 接下来，定义了对坐标的曲线积分。它是一种极限过程，考虑的是在平面上的有向光滑曲线弧L上，对于函数Px(x, y)和Qy(x, y)，分别沿着x和y坐标方向的积分。这种积分可以理解为对曲线L上的向量场F=(Px, Qy)进行积分，结果是一个标量值，表示了F沿着L的线积分。积分的定义包含了路径的选取，方向的考虑，以及函数在L上的连续性和曲线的光滑性。 在计算对坐标的曲线积分时，我们有一个重要的定理：如果函数P(x, y)和Q(x, y)在曲线L上连续，并且L可以用参数方程x=φ(t), y=ψ(t)来表示，那么积分可以通过参数形式来计算。具体来说，积分可以转化为对参数t的积分，即∫[a, b] P(φ(t), ψ(t))φ'(t) dt + ∫[a, b] Q(φ(t), ψ(t))ψ'(t) dt。这里的φ'(t)和ψ'(t)是非零的，保证了曲线的光滑性。 对坐标的曲线积分具有一些重要的性质。一是积分的路径方向性，即积分的结果可能因曲线方向的不同而不同。二是路径的可加性，如果一条曲线可以分为几段，则整体的积分等于各段积分的和。三是线性性质，积分对被积函数的线性组合也满足线性性质。 总结起来，对坐标的曲线积分是微积分中的一个重要工具，用于处理曲线上物理问题的计算，如力的功，它涉及到了极限、微元法、参数方程以及积分的路径依赖性和线性性质等基本概念。理解和掌握这些知识点，对于解决实际问题以及进一步学习多元函数的积分理论至关重要。