林轩田《机器学习基石》课程笔记5 -- Training versus Testing1

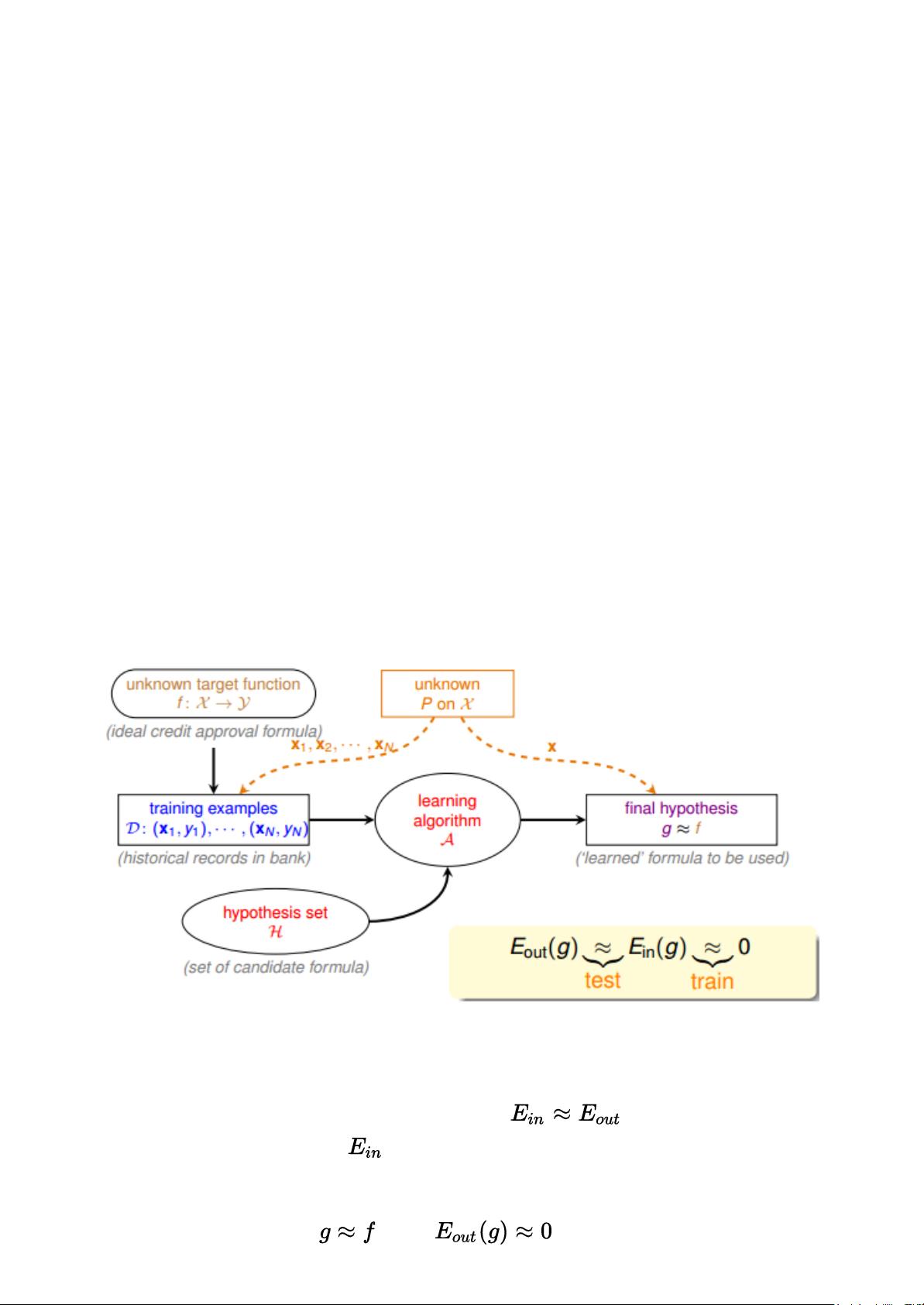
在《机器学习基石》课程笔记5中，作者探讨了机器学习中的核心问题——Training与Testing，以及它们在无限Hypothesis Set情况下的可行性。机器学习的目标是找到最佳的函数g，使得训练误差（training error）尽可能小，并且期望误差（expected error）也小，从而确保模型具有良好的泛化能力。 在前四节课中，课程主要围绕以下几个要点展开： 1. **机器学习定义**：机器学习旨在通过数据找到最佳函数g，最小化损失函数L。 2. **可行性条件**：基于NFL定理，若样本量足够大且假设空间（hypothesis set）有限，机器学习是可行的。这依赖于霍夫丁不等式，它保证了在大量数据下，即使存在很多假设，也可以避免因“Bad Data”导致的错误。 3. **算法应用**：介绍了如PLA（Perceptron Learning Algorithm）和Pocket算法等，用于解决监督学习中的二元分类问题。 4. **统计学联系**：利用统计学原理，将学习算法与概率理论相结合，证明在特定条件下，机器学习的期望误差可近似等于训练误差。 课程接着讨论了Hypothesis Set的大小（M）对机器学习的影响： - **M较小**：霍夫丁不等式保证了低的训练误差，但由于选择的假设有限，可能无法找到使期望误差也极小的hypothesis。 - **M较大**：训练误差可能高，因为假设之间的差距大，但更大的M可能使得找到低期望误差的假设成为可能。 关键在于找到合适的M值，使其既能保证训练误差小，又能确保泛化性能。当M无限大时，问题在于如何处理无限假设空间。作者通过分析PLA算法，指出虽然直线的数目是无限的，但通过限制有效假设（Effective Number of Hypotheses）到有限个，依然可以保证学习的可能性。 为了量化有效假设的数量，文章举例分析了在二维平面上划分点的直线种类。随着点的数量增加，尽管总的直线种类看似无限，但实际上有效直线数量的增长受到限制，满足一定的函数关系，如2^N-2。这种分析表明，即使面对无限假设空间，只要能有效地限制实际参与决策的假设数量，机器学习仍然是可行的。 总结来说，机器学习的核心挑战在于平衡训练误差和泛化能力，这涉及到假设空间的大小、数据量以及数据分布。通过统计学方法和对无限假设空间的有效处理，可以确保机器学习在实际应用中具备良好的学习效果。这一节课程深化了对机器学习可行性的理解，揭示了在理论和实践中如何处理复杂性与效率之间的权衡。