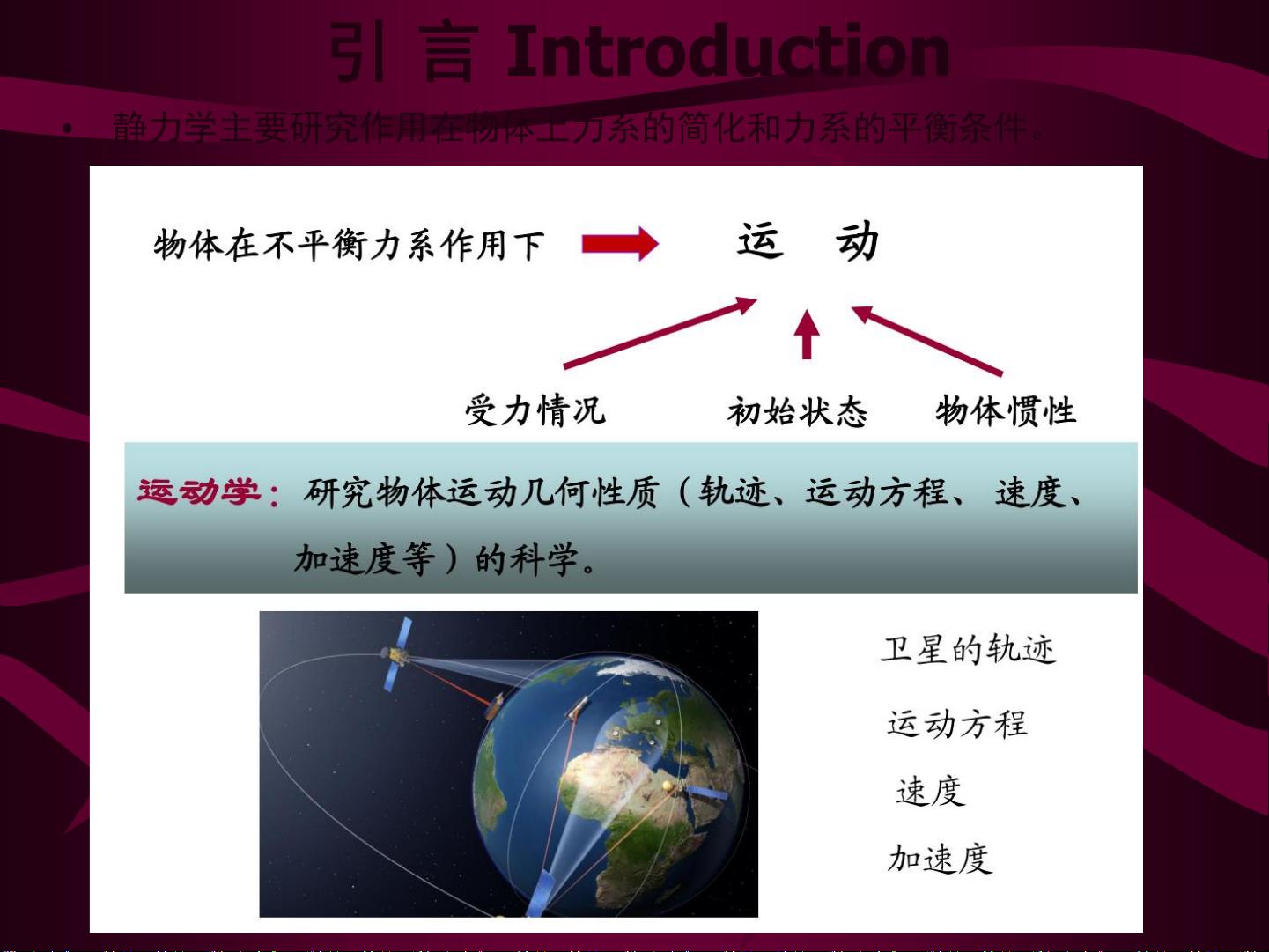
【运动学】是物理学的一个分支，它专注于研究物体运动的几何特性，而不涉及引起这些运动的原因，即不涉及力和能量。运动学的核心任务包括分析物体的轨迹、运动方程、速度和加速度。
【点的运动学】是运动学的一个特例，专门研究质量可忽略不计的点状物体，即质点的运动。质点的理想化模型用于简化分析，当物体的尺寸在描述运动时变得不重要时，我们将其视为质点。
【轨迹】是点在空间运动所经过的路径。它可以是直线（直线运动）或曲线（曲线运动）。直线运动是最简单的运动形式，而曲线运动则更为复杂，如圆周运动或抛体运动。
【位置矢量】(r)表示质点相对于固定参考点（如坐标原点O）的位置，它随时间变化，是时间的单值连续函数。矢径的末端描绘了质点的运动轨迹。
【速度】是描述质点运动快慢和方向的矢量量。平均速度是在时间间隔Δt内物体位移与时间的比值，而瞬时速度是当Δt趋近于零时的极限，即速度矢量等于位置矢量对时间的一阶导数。速度的方向沿着轨迹的切线。
【加速度】是速度的变化率，是速度矢量对时间的导数，或者说是位置矢量对时间的二阶导数。加速度同样具有方向和大小，反映了物体速度变化的快慢和方向。
【直角坐标法】是描述点运动的常用方法，通过建立直角坐标系，将位置矢量分解为x、y、z三个分量，每个分量都随时间变化。运动方程可以表示为x=f1(t), y=f2(t), z=f3(t)，其中f1、f2、f3是时间t的函数。轨迹方程可以通过消去时间变量得到。
【速度的大小】(Magnitude of Velocity)是速度矢量的标量值，可以由x、y、z分量的时间导数的平方和的平方根表示。
【方向余弦】(Direction Cosines of Velocity)是速度矢量在直角坐标轴上的投影与对应轴单位矢量之间的夹角的余弦值，它们给出了速度在各个坐标轴上的分量比例。
运动学提供了描述质点在空间中如何运动的数学工具，从轨迹、速度到加速度，这些都是理解和分析更复杂物理现象的基础。在实际应用中，如机械设计（如曲柄滑块机构）和游乐设施（如过山车）的设计，都需要对这些基本概念有深入的理解。
评论0