67.最全的机器学习中的优化算法介绍 - 起风之后，只剩沙丘 - CSDN博客1

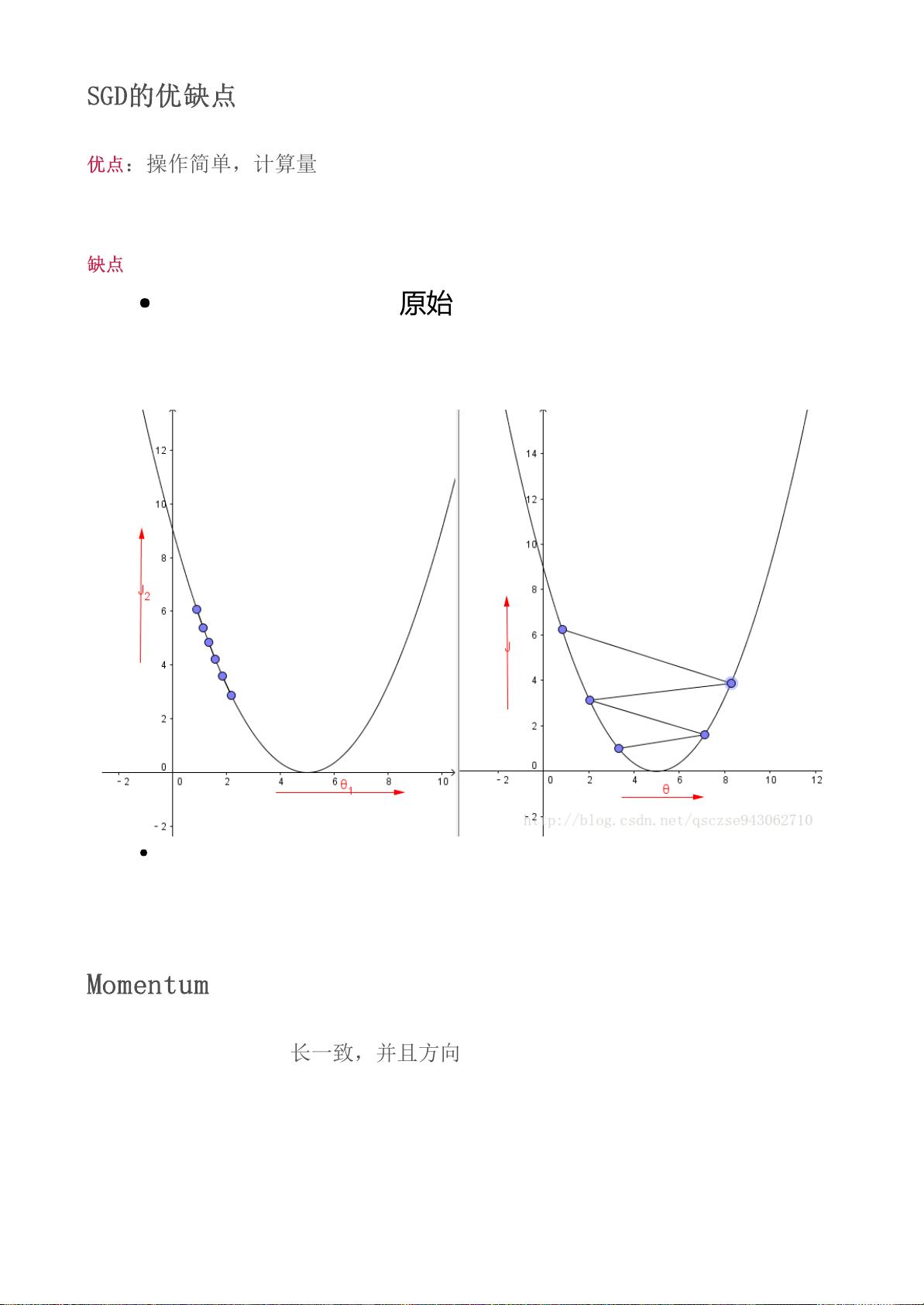
在机器学习领域，优化算法是寻找模型参数最优值的关键技术，尤其当问题没有解析解或解析解计算复杂度高时。本文将详细讲解几种常见的优化算法，包括梯度下降法、Momentum算法、Nesterov Momentum（NAG）以及共轭梯度法。 梯度下降法是最基础的优化算法，其核心思想是沿着目标函数梯度的反方向前进，以最快的速度减小损失函数。在第n次迭代中，参数更新公式为：θn = θn−1 + Δθ，其中Δθ = −αL′(θn−1)，α是学习率。梯度下降法有全量、批量和随机三种形式，分别处理不同规模的数据集。 接着，Momentum算法是为了改进SGD的收敛稳定性和跳出局部最优的能力。它引入了一个动量项，保留了部分前一次的更新方向，更新公式为：Δθn = ρΔθn−1 + gn−1，θn = θn−1 − αΔθn。ρ是动量系数，通常在[0, 1]之间，可以避免SGD的剧烈震荡。 Nesterov Momentum（NAG）进一步优化了Momentum，它提前预测了一步后的梯度方向，使得更新更加前瞻。NAG的更新公式为：Δθn = ρΔθn−1 + g(θn−1−αΔθn−1)，θn = θn−1 − αΔθn。这种方式利用了二阶导数信息，可以更快地收敛于最优解。 共轭梯度法（Conjugate Gradient）针对线性方程组的优化，它在每次迭代中选取与之前梯度共轭的方向进行更新，减少了计算步骤，尤其适用于低维度问题。CG的优点在于不需要矩阵逆运算，适用于大型稀疏矩阵，但不适用于高维问题。 这些优化算法各有优缺点，适应不同的场景。例如，梯度下降法简单易用，但可能陷入局部最优；Momentum和NAG提高了收敛速度，但增加了超参数的选择难度；共轭梯度法在某些情况下效率高，但不适合高维空间。在实际应用中，通常需要结合问题特性及实验效果来选择合适的优化算法。 总结来说，机器学习中的优化算法是模型训练的关键，它们通过迭代更新参数来最小化损失函数，包括梯度下降法及其变体如Momentum和NAG，以及特定情况下的高效算法如共轭梯度法。理解这些算法的工作原理和特点，有助于我们更好地解决实际的机器学习问题。