7.3兰伯特余弦定理1

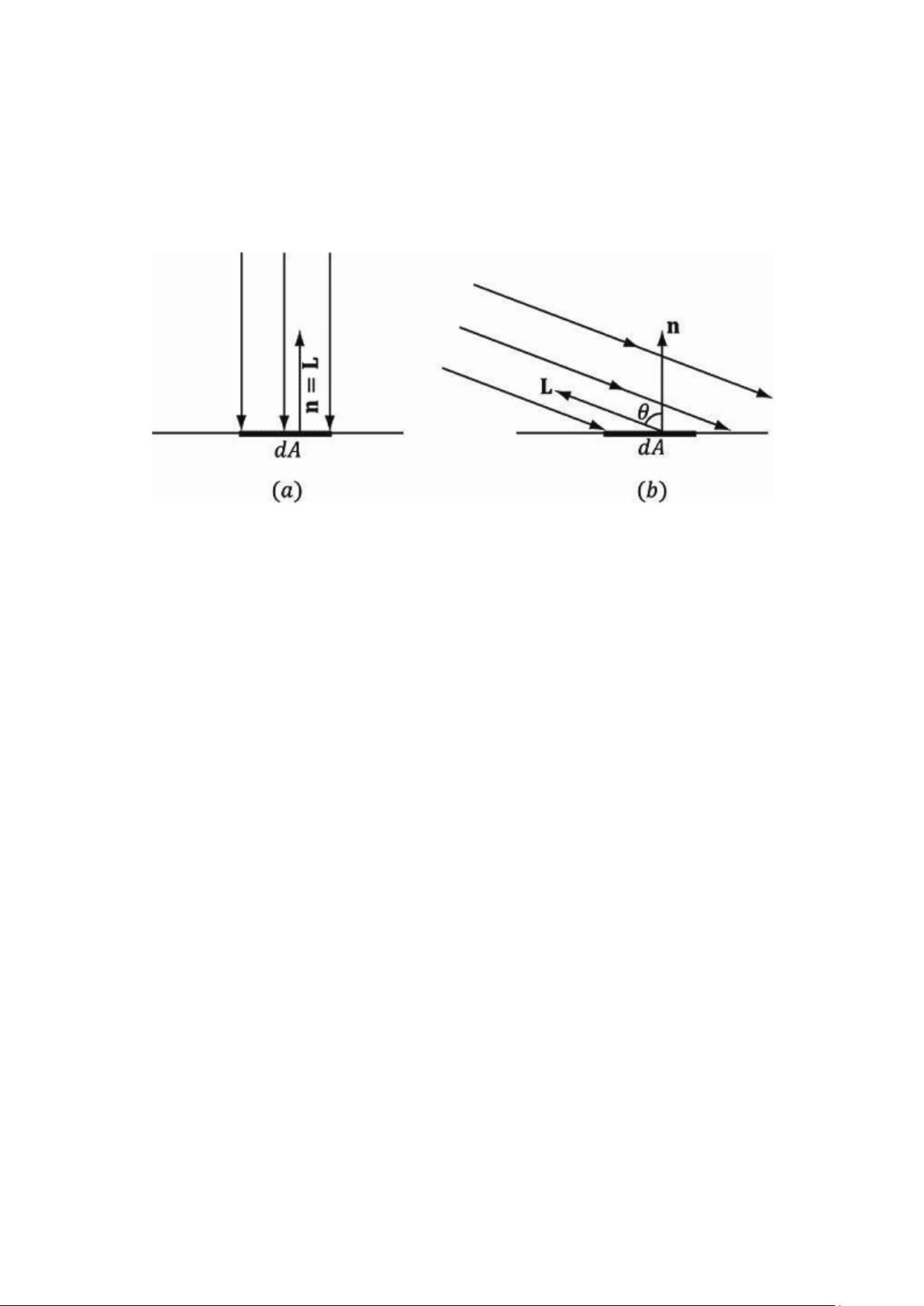
兰伯特余弦定理是计算机图形学中用于模拟真实世界光照效果的重要理论，尤其在三维渲染和物理基础光照模型的构建中起着关键作用。这个定理涉及到光线与物体表面之间的相互作用，以及如何根据它们之间的相对角度来计算接收到的光强。 在描述中提到，兰伯特余弦定理解释了为何垂直于光源的表面接收到的光强比侧面照射的要强。这是因为光线与表面法线之间的夹角决定了有多少光线能直接投射到表面。法线是指垂直于表面的向量，而光照向量是从光源指向表面的向量。当这两个向量之间的夹角θ增大时，有更多的光线偏离了表面，导致照射到表面的光线减少。 兰伯特余弦定理的数学表示为： \[ f(\theta) = \max(\cos\theta, 0) = \max(\mathbf{L} \cdot \mathbf{n}, 0) \] 在这个公式中，\( \mathbf{L} \) 是单位向量表示光照向量，\( \mathbf{n} \) 是单位向量表示法线向量，\( \theta \) 是这两个向量之间的夹角。\( \mathbf{L} \cdot \mathbf{n} \) 是向量的点积，其结果是两个向量之间夹角的余弦值。由于点积的结果范围在 -1 到 1 之间，当夹角为 0º 时（即 \( \mathbf{L} \) 与 \( \mathbf{n} \) 同向），余弦值为 1，表示最大的光照强度；而当夹角为 90º 或更大时，余弦值为 0 或负数，表示没有光线直接照射到表面。因此，我们用 \( \max \) 函数确保当夹角超过 90º 时，光照强度为 0，这意味着光线来自物体的背面，不会产生光照。 图 7.9 显示了 \( f(\theta) \) 随 \( \theta \) 变化的曲线，表明当角度在 -90º 到 90º 之间变化时，光照强度在 0%（0.0）到 100%（1.0）之间变化。请注意，角度是以弧度表示的，因此 π/2（约 1.57）对应 90º。 在实际应用中，兰伯特余弦定理常用于基本的漫反射（diffuse）光照模型，它简化了计算，使我们能够快速估算物体表面的亮度。在游戏开发、虚拟现实、电影特效等领域，这个定理是实现逼真光照效果的基础之一。通过结合其他光照模型，如镜面反射（specular reflection）和环境光（ambient light），我们可以创建更加复杂的光照效果，进一步提升视觉体验。