新教材_zyj_chapter+8+New1

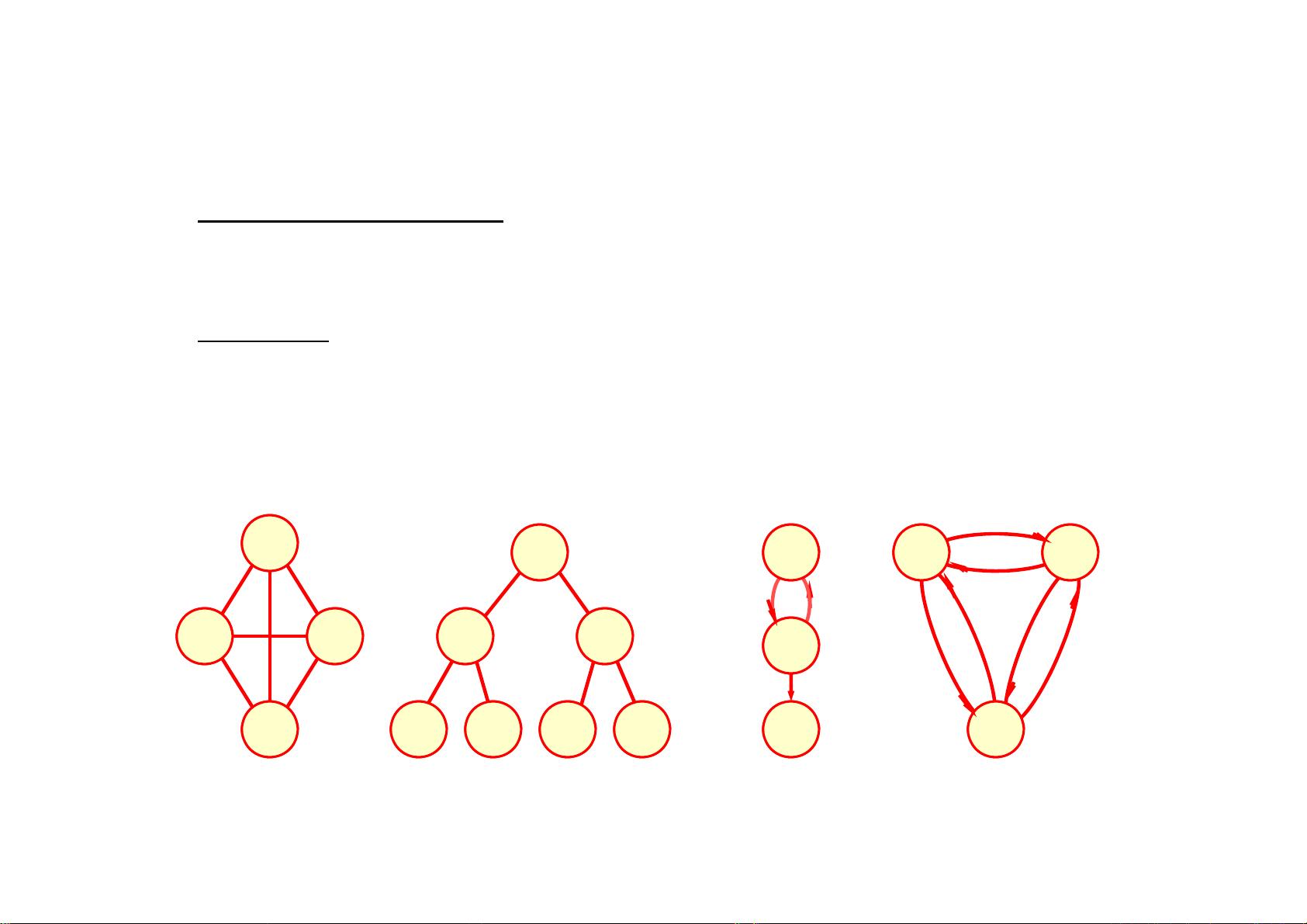
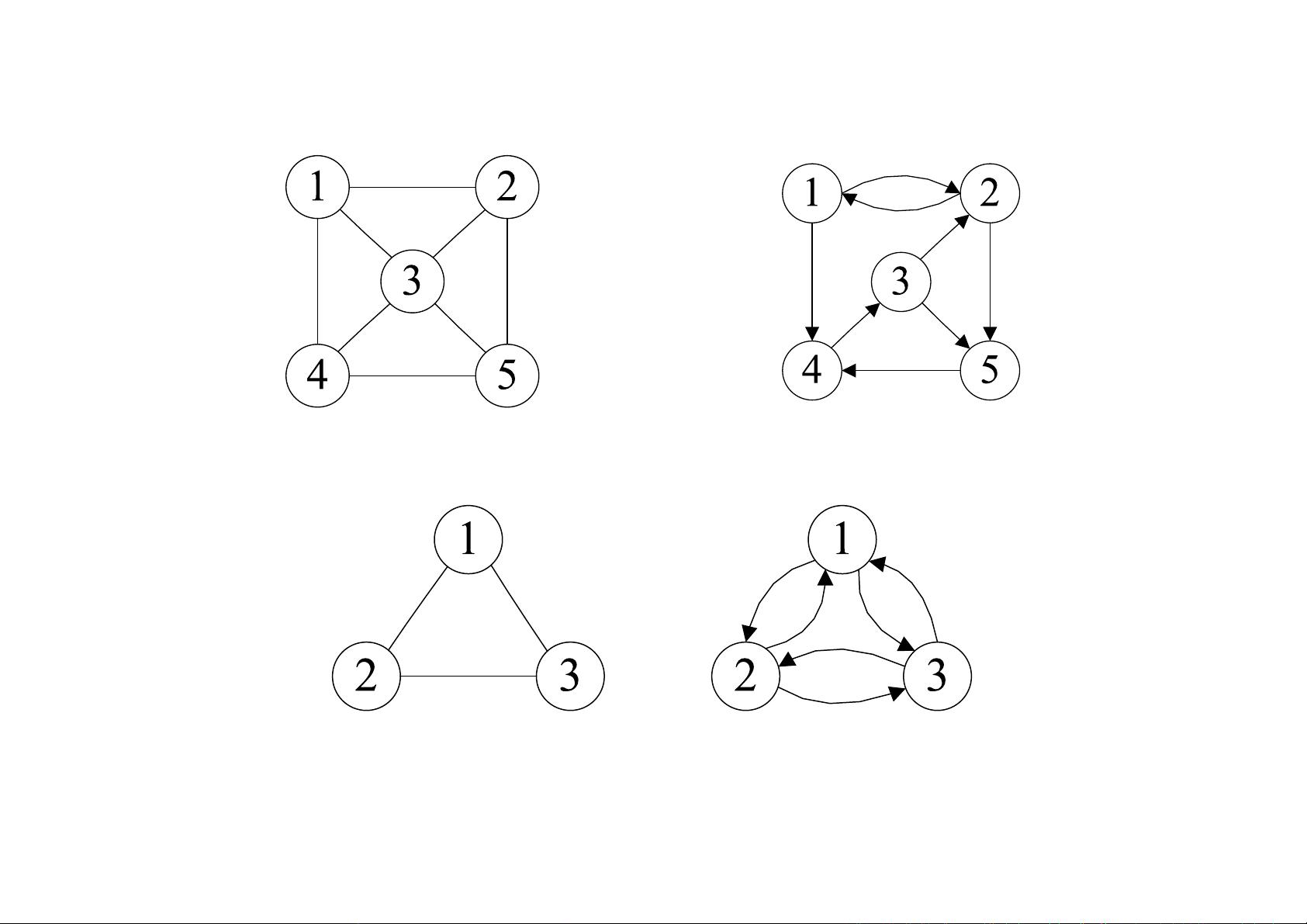
"图的基本概念和存储结构" 图是由顶点集合(vertex)及顶点间的关系集合组成的一种数据结构：Graph＝(V, E)其中，V={x|x某个数据对象}是顶点的有穷非空集合；E={(x, y)|x, yV}或E={<x, y>|x, yV && Path(x, y)}是顶点之间关系的有穷集合，也叫做边(edge)集合。Path(x, y)表示从x到 y的一条单向通路，它是有方向的。 图可以分为有向图和无向图两种。在有向图中，顶点对<x, y>是有序的。在无向图中，顶点对<x, y>是无序的。完全图是指有n个顶点的无向图有n(n-1)/2条边的图，有n个顶点的有向图有n(n-1)条边的图。 图中有两个重要概念：邻接顶点和子图。邻接顶点是指(u, v)是E(G)中的一条边，则称u与v互为邻接顶点。子图是指设有两个图G＝(V, E)和G’＝(V’, E’)，若V’V且E’E，则称图G’图G的子图。 权是一些图的边具有与它相关的数，称之为权。这种带权图叫做网络。在图中，每个顶点都有一个度，表示与它相关联的边的条数。顶点的度等于该顶点的入度与出度之和。在有向图中，顶点的入度是以v为终点的有向边的条数，顶点的出度是以v为始点的有向边的条数。 路径是在图G＝(V, E)中，若从顶点vi出发，沿一些边经过一些顶点vp1, vp2, …, vpm，到达顶点vj，则称顶点序列(vi vp1 vp2 ... vpm vj)为从顶点vi到顶点vj的路径。路径长度非带权图的路径长度是指此路径上边的条数。带权图的路径长度是指路径上各边的权之和。简单路径是指路径上各顶点v1, v2, ..., vm均不互相重复的路径。回路是指路径上第一个顶点v1与最后一个顶点vm重合的路径。 图的连通性是一个重要概念。在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与v2是连通的。如果图中任意一对顶点都是连通的，则称此图是连通图。非连通图的极大连通子图叫做连通分量。在有向图中，若对于每一对顶点vi和vj，都存在一条从vi到vj和从vj到vi的路径，则称此图是强连通图。非强连通图的极大强连通子图叫做强连通分量。如果有向图G的每对顶点v和w，有一个由不同顶点组成的顶点序列<v0,v1, …, vk>，其中v0=v, vk=w且<vi, vi+1>∈E(G)或者<vi+1, vi>∈E(G) (0≤i<k)，则称有向图G是弱连通的。非弱连通图的极大弱连通子图叫做弱连通分量。 图的存储结构有多种，邻接矩阵是一种常用的存储结构。设图A=(V, E)是一个有n个顶点的图，图的邻接矩阵是一个二维数组A.edge[n][n]，定义：邻接矩阵 (Adjacency Matrix) , ),( , ,]][[ .否则或者如果0><1AEjiEj 生成树是图的一种重要应用。生成树是指一个连通图的生成树是其极小连通子图，在n个顶点的情形下，有n-1条边。强连通图和弱连通图的生成树也是一种重要的应用。 拓扑排序是指在一个有向无环图中，对所有顶点进行排序，使得对于每一对顶点u和v，如果有从u到v的路径，则u在v之前出现。关键路径是指在一个有向无环图中，从源点到达汇点的最长路径。最短路径是指在一个有向图中，从源点到达汇点的最短路径。