20151910042-刘鹏-IT实验1-图形绘制1
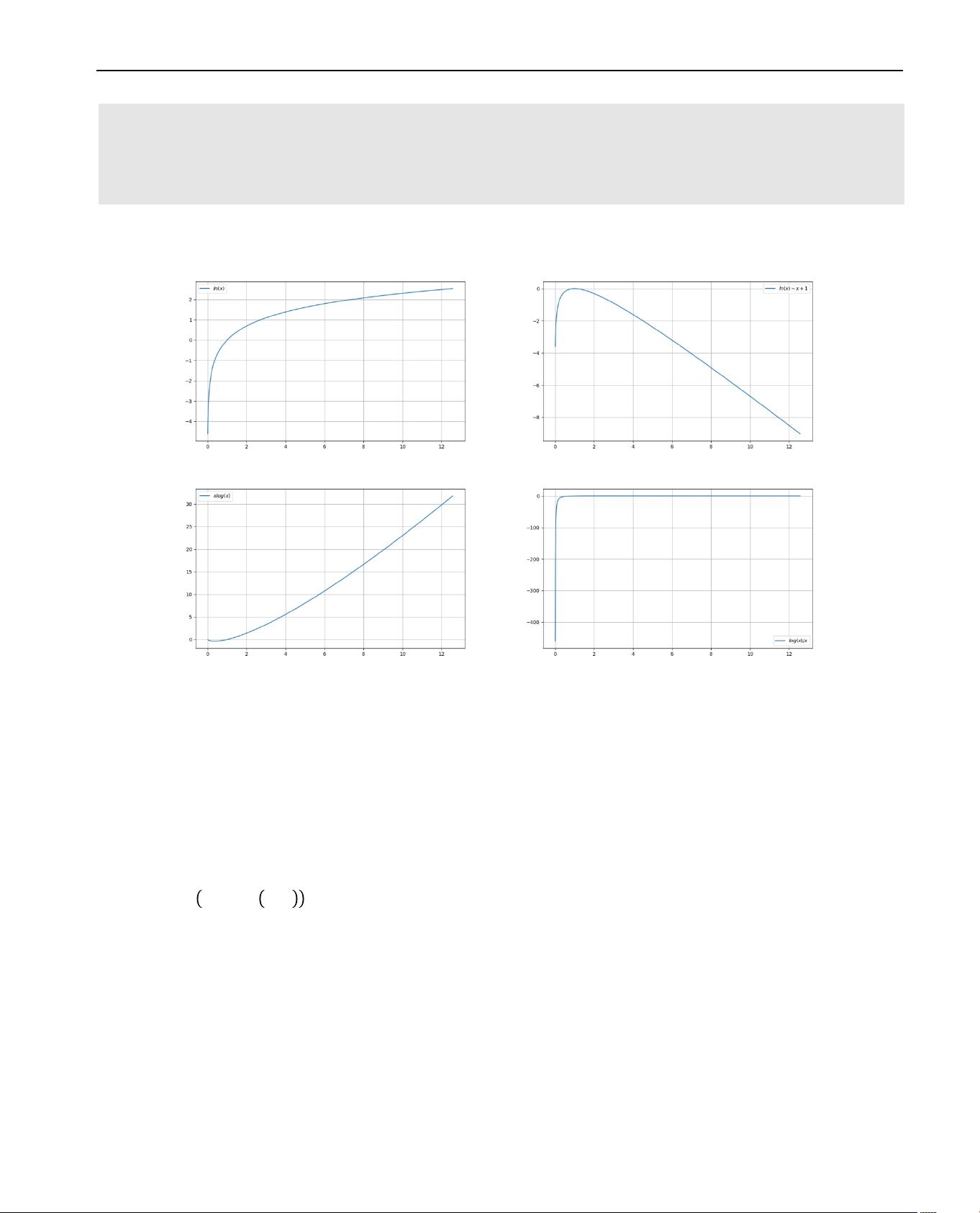
这篇文档是关于云南大学数学与统计学院数学系信息与计算科学专业的一次上机实践报告,主题是“信息论基础实验”,由学生刘鹏完成。实验的主要目的是通过绘制信息论中常用的函数图形来熟悉这些函数的特性,并为后续学习提供直观的理解。实验使用了Windows 10操作系统,Python 3.6.0编程语言,以及Wing IDE Professional 6.0.5-1作为集成开发环境。 实验内容涵盖了九个函数的图形绘制,其中包括对数函数及其变体,熵(Entropy)H(x),相对熵(Kullback-Leibler Divergence)D(p||q),以及互信息(Mutual Information)I(X;Y)。以下是每个函数的简要介绍: 1. **y = ln(x)**:自然对数函数,随着x值的增加,y值从负无穷逐渐逼近正无穷,曲线在x=0处没有定义,但随着x趋近于0,y趋近于负无穷。 2. **y = ln(x) - x + 1**:这是对数函数与线性函数的组合,其图形在x=1处有极大值。 3. **y = xln(x)**:这是x与ln(x)的乘积,图形在x=0处没有定义,随着x的增大,y值先增加后减小,具有一个最大值。 4. **y = ln(x)x**:这个函数的图形在x=1时达到最大值,且在x=0时没有定义。 5. **y = H(x) = ―xln(x) ― (1 ― x)ln(1 ― x)**:熵函数,表示信息的不确定性,它在x=0.5时达到最小值,反映了均匀分布的不确定性最高。 6. **D(p||q)**:相对熵,衡量两个概率分布p和q的差异,无法直接画图,因为需要具体定义p和q。 7. **D(p||p)**:当两个分布相同时,相对熵为0,表示没有差异。 8. **I(X;Y) given p(y|x)**:条件互信息,衡量X和Y在已知Y的条件下相互依赖的程度。 9. **I(X;Y) given p(x)**:互信息,衡量X和Y的独立程度,即使得其他变量不变时,X和Y的联合熵与它们的边际熵之差。 在实验过程中,刘鹏使用了Python的numpy库生成数据,并用matplotlib的pyplot库绘制了前四个函数的图形,展示了如何用编程方法可视化这些信息理论中的关键函数。然而,对于后面几个涉及概率分布的函数,由于需要具体定义概率分布,因此没有直接的图形展示,需要更复杂的分析和计算。 这次实验是信息论学习的一个基础练习,通过可视化手段加深了对信息理论中核心概念的理解。这种实践教学方法有助于学生掌握理论知识并提升实际操作能力。


剩余19页未读,继续阅读
- 粉丝: 42
- 资源: 342
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 02-【管理流程】-30-薪酬发放流程图.docx
- 行为驱动开发 (BDD) 和 Tes 质量指标的比较数据集-最新出炉.zip
- IMF分量显著性检验:EEMD分解中的真实信号判别与能量谱属性分析,imf的显著性检验 对输入信号进行eemd分解,然后对imf分量进行显著性检验 文中的蓝线是0.05置信区间,红线是0.01置信
- 基于MPC与ADRC的车速控制算法研究:实现期望加速度与节气门制动控制,适用于燃油汽车,可用于实车试验与车速需求控制,附带复现资料 ,基于模型预测MPC和自抗扰adrc实现的车速控制,控制目标为燃油汽
- 各种企业与员工解除和终止劳动合同通知书.docx
- 《解除劳动合同协议书》两范本及说明.doc
- 解除劳动合同的情形及程序.xlsx
- 解除或终止劳动合同通知书.doc
- 解除劳动合同通知工会函.doc
- 解除劳动合同通知书(单方解除).docx
- 解除劳动合同协议书.doc
- 解除劳动合同书(最新).doc
- 解除劳动合同协议书(正常离职版).doc
- 旷工解除劳动合同的模板-公告、通知书.docx
- 劳动合同解除协议(主动离职).doc
- 终止解除劳动合同通知书(全套).doc


 信息提交成功
信息提交成功
评论0