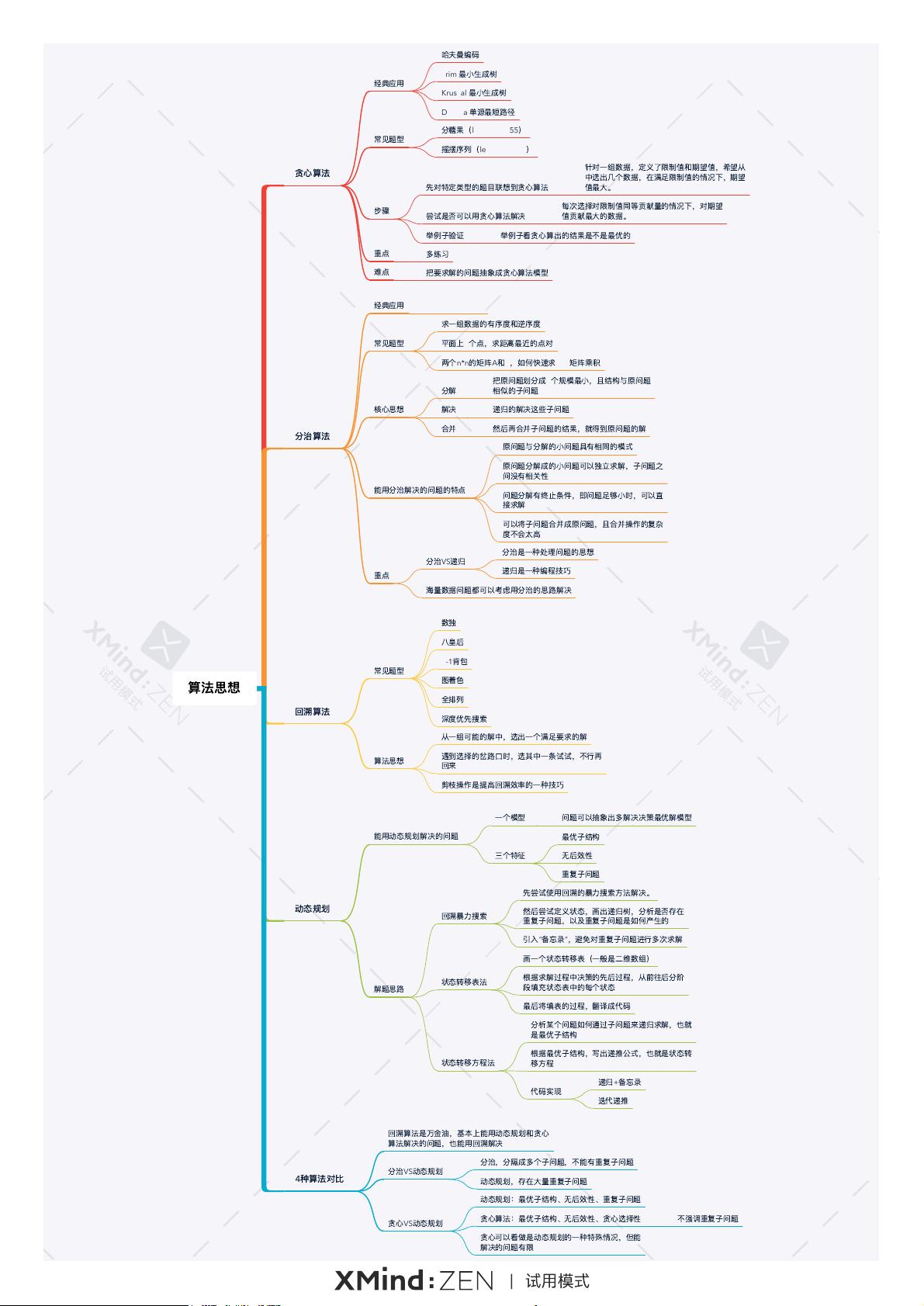
四大算法思想1
需积分: 0 191 浏览量
更新于2022-08-03
收藏 267KB PDF 举报
在计算机科学中,算法是解决问题的关键工具,它们指导着程序如何高效地执行任务。本文将深入探讨四种重要的算法思想:贪心算法、分治算法、回溯算法和动态规划。
贪心算法是一种策略,它在每一步选择局部最优解,期望最终达到全局最优解。在实际应用中,贪心算法常用于资源优化问题,如哈夫曼编码,它构建最高效的二进制前缀码。此外,Prim和Kruskal算法用于寻找图的最小生成树,Dijkstra算法则用于寻找图中单源最短路径。在解决这类问题时,我们需要先定义问题的限制值和期望值,然后尝试通过贪心策略选择最优解。例如,分糖果问题(LeetCode 455)和摇摆序列问题(LeetCode 376),都可以用贪心算法求解。关键在于正确地抽象问题并设计合适的贪心策略,但贪心算法并不总是能保证得到全局最优解,因此需要通过实例验证其有效性。
分治算法的核心是将大问题分解为小问题,然后递归解决这些小问题,最后将结果合并。这种方法在处理规模相同且相互独立的子问题时非常有效,如MapReduce框架就体现了分治思想。常见的分治问题包括计算数据的有序度和逆序度、寻找平面上最近的点对,以及快速矩阵乘法。分治算法的关键在于问题必须有终止条件,且子问题的解能够合并为原问题的解,而合并操作的复杂度相对较低。
回溯算法是一种试探性的解决问题的方法,它尝试所有可能的解决方案,遇到无效的解时会回退到上一步,继续尝试其他分支。典型的回溯问题包括数独、八皇后、0-1背包、图着色和全排列。回溯算法通常结合深度优先搜索(DFS)使用,并通过剪枝技术减少无效的搜索。为了提高效率,可以使用记忆化搜索,即备忘录技术,避免重复计算已解决的子问题。
动态规划是解决具有最优子结构、无后效性和重复子问题的问题的有效手段。动态规划通过构建状态转移表或状态转移方程,逐步求解问题。例如,斐波那契数列、最长公共子序列和背包问题都可以用动态规划解决。在实际应用中,我们首先尝试暴力回溯,然后定义状态,分析最优子结构和重复子问题,最后使用备忘录或迭代递推的方式实现算法。动态规划与贪心算法的区别在于,贪心算法不考虑后续决策的影响,而动态规划则需要考虑到整个决策过程。
总结起来,这四种算法思想各有特点,回溯算法适用于多种问题,但效率相对较低;分治算法适用于可分解为独立子问题的问题;贪心算法在满足特定条件下能找到局部最优解,但不保证全局最优;动态规划则能解决存在大量重复子问题的问题,通过存储子问题的结果避免重复计算。理解并熟练掌握这些算法,对于解决复杂的编程问题至关重要。在实践中,需要根据问题的具体特性灵活选用合适的算法,以实现最有效的解决方案。
挽挽深铃
- 粉丝: 19
- 资源: 274
最新资源
- 电动汽车模型的各模块的Simulink模型,包括驾驶员模块,整车控制器模块,电机模块,变速器模块,主减速器模块,车轮模块,车速模块以及BMS模块 附有说明文档,文档详细的描述了模型的建模过程及功能
- 西门子200smart与东元Teco N310变频器通讯实战程序 器件:西门子s7 200 smart PLC,东元Teco N310变频器,昆仑通态触摸屏(带以太网),中途可以加路由器
- 三菱FX3U 485ADP与东元TECO变频器N310通讯实战程序 功能:通过三菱fx3u 485ADP-MB板对东元Teco N310变频器进行modbus通讯,实现频率设定,启停控制,输出
- 【Matlab Simulink】电动汽车双向充电桩电路仿真 交流侧采用普通三相桥式变电路,SVPWM控制生成开关信号,控制系统采用电压外环电流内环控制 可实现整流,逆变以及指定功率输出,无功补偿 直
- 基于MATLAB的圆形检测算法:在MATLAB中实现的,利用图像边缘的梯度信息 进行圆形检测的算法m文件可直接运行 相比于传统的霍夫变检测圆的算法速度有极大提升
- 电动汽车充电站选址定容Matlab程序代码实现 在一定区域内的电动汽车充电站多目标规划选址定容的Matlab程序 使用PSO和Voronoi图联合求解
- 基于遗传算法的电动汽车有序充电优化调度 软件:Matlab 利用遗传算法对电动汽车有序充电进行优化;优化目标包括充电费用最低,电动汽车充到足够的电,负荷峰谷差最小 分别利用传统、精英和变异遗传算法进
- 无迹卡尔曼滤波UKF,平方根无迹卡尔曼滤波SRUKF,自适应平方根无迹卡尔曼滤波ASRUKF估算电池SOC
- 多目标粒子群算法CCHP联供综合能源系统 说明书MATLAB代码:基于多目标粒子群算法冷热电联供综合能源系统运行优化关键词:综合能源 冷热电三联供 粒子群算法 多目标优化参考文档:基于多目标算法的
- 运用Matlab,LBP分割脸部特征,从而达到识别人物面部表情的效果
- FPGA Verilog 舵机驱动代码,FPGA驱动舵机
- 西门子S7-1500PLC与西门子V90 PN伺服通讯控制项 西门子S7-1500PLC与西门子V90 PN伺服通讯控制项目程序项目程序包含S7-1500 PLC,KTP系列触摸屏,西门子V90 PN
- 碳交易机制下考虑需求响应的综合能源系统优化运行 首先,根据负荷响应特性将需求响应分为价格型和替代型 2 类,分别建立了基于价格弹性矩阵的价格型需求响应模型,及考虑用能侧电能和热能相互转的替代型需求响应
- 质子交膜燃料电池系统模型(PEMFC),基于MATLAB simulink开发 主要部分有空压机模型,供气系统模型(阴极和阳极),背压阀模型,电堆模型等 可进行控制策略等仿真开发工作
- 基于.net6的跨平台物联网网关 通过可视化配置,轻松的连接到你的任何设备和系统(如PLC、扫码枪、CNC、数据库、串口设备、上位机、OPC Server、OPC UA Server、Mqtt Se
- 不确定性决策理论及其军事与自动化应用