D11_6高斯公式1

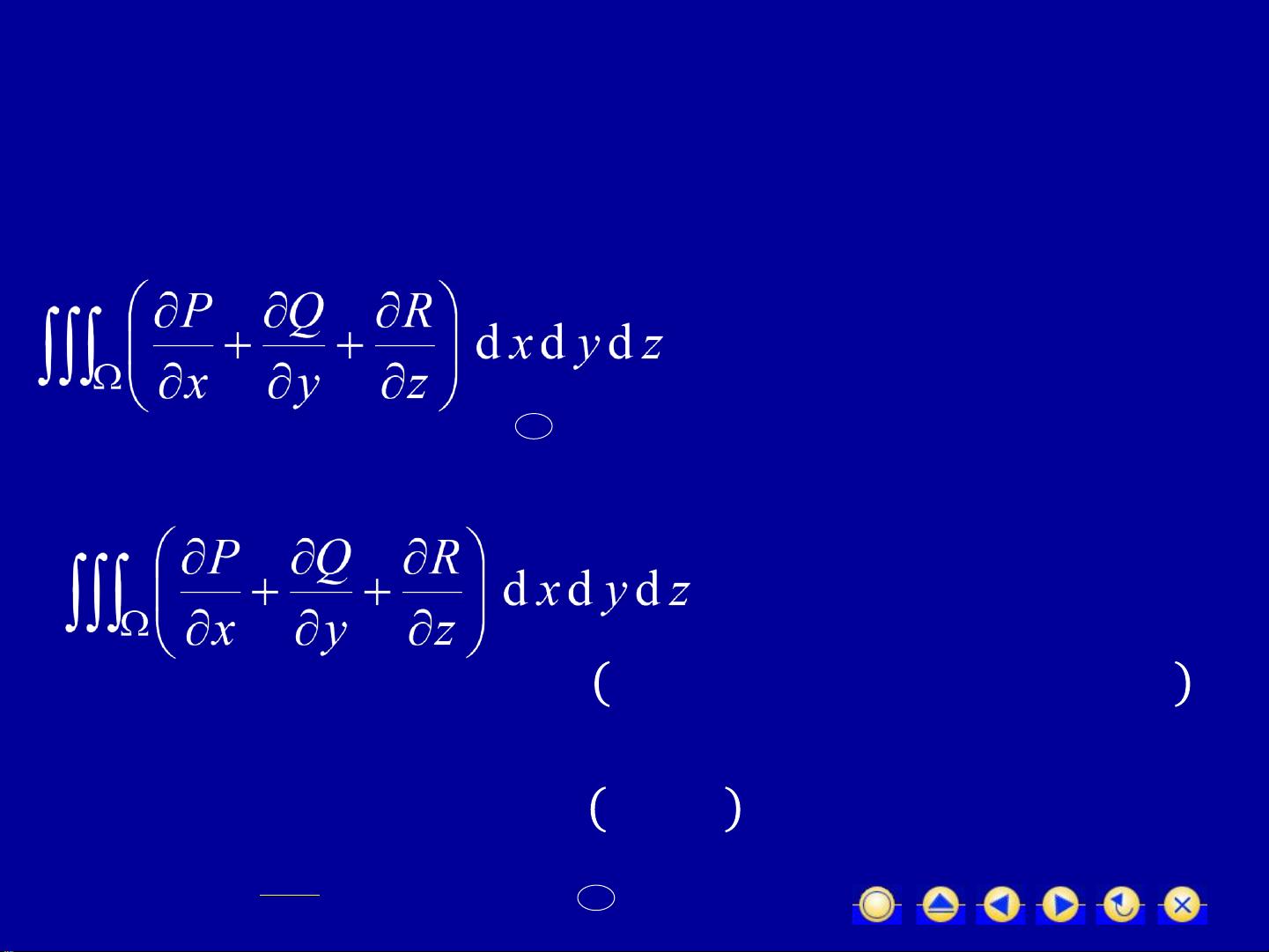
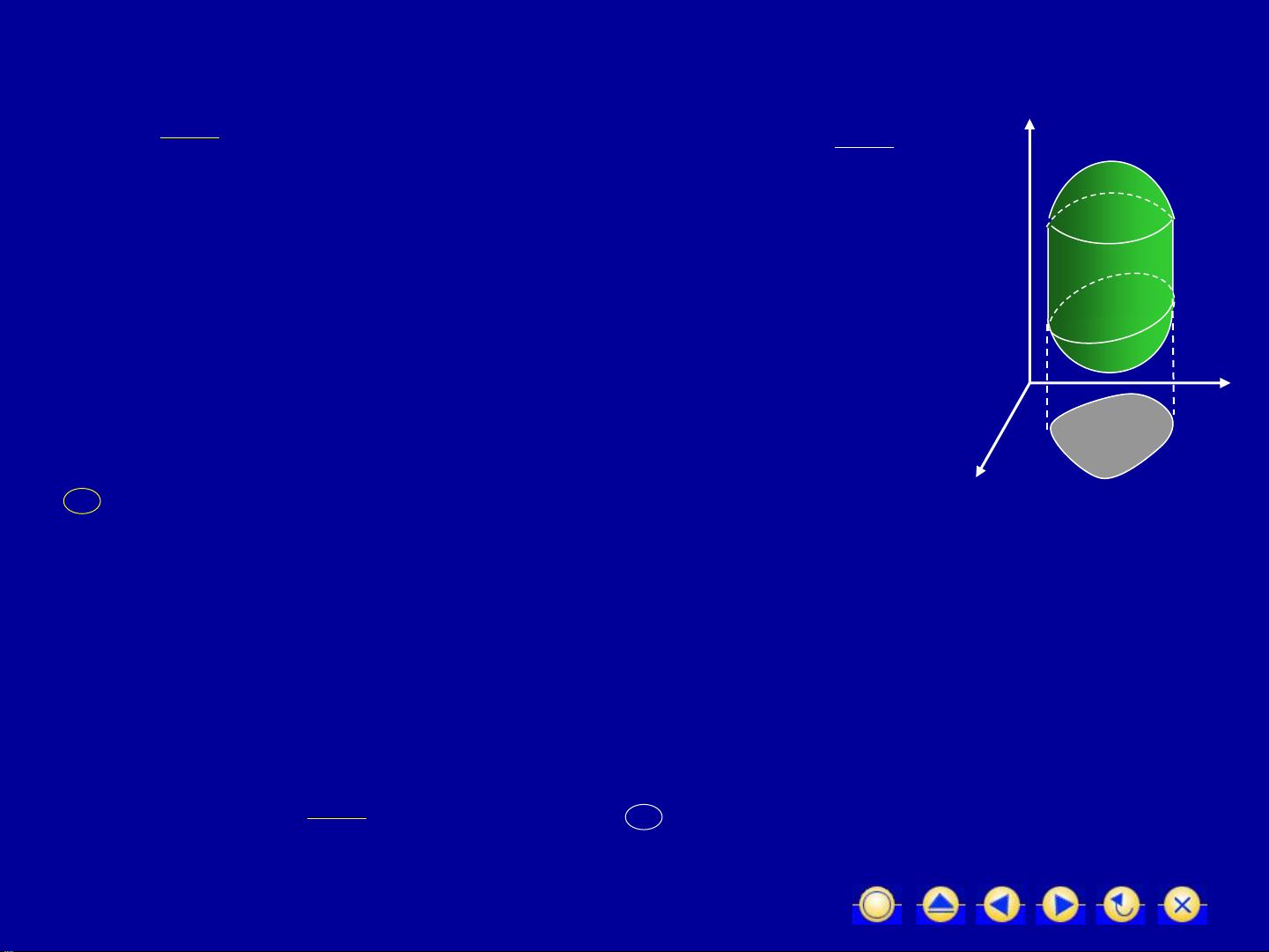
高斯公式是多元微积分中的一个核心定理，它建立了空间闭区域上的三重积分与其边界曲面上的曲面积分之间的关系。这个公式是Green公式和Stokes公式的三维版本，对于理解和应用数学物理中的积分变换有着至关重要的作用。 标题中的"D11_6高斯公式1"可能指的是课程或者教材的章节编号，其中"6"可能是第六节，而"D11"可能是该系列课程的第11单元。描述中提到的是Green公式和Gauss公式的推广，这通常出现在高等数学或流形微积分的教学中。 高斯公式的基本形式可以表示为： 如果函数P, Q, R在闭区域Ω上有连续的一阶偏导数，并且Ω由分片光滑的封闭曲面Σ所包围，那么有： \[ \iiint_{\Omega} (\frac{\partial R}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial P}{\partial z}) dV = \iint_{\Sigma} (P \cos \alpha + Q \cos \beta + R \cos \gamma) dS \] 其中，\( \alpha, \beta, \gamma \) 是Σ上每一点处外法向量的方向余弦，dS表示曲面Σ上的微元面积，dV是体积元素。 这个公式表明，一个闭区域内的三重积分可以转化为该闭区域边界曲面上的曲面积分。这在计算某些复杂的积分问题时提供了便利，尤其是在处理涉及散度的物理问题时，如电场通量、流体的流量等。 标签"平面"提示我们讨论的主要是二维情况，但高斯公式是在三维空间中的概念，它扩展了平面Green公式的思想，将积分从二维区域扩展到三维空间。 部分内容中列举了几个例子，展示了如何应用高斯公式来计算曲面积分。例如，第一个例子中，计算锥面和平面所围成的区域的边界曲面积分，第二个例子使用高斯公式计算柱面闭域的边界曲面积分，第三个例子则是在球形区域内的积分转换。 总结来说，高斯公式是微积分中用于连接三维区域内部积分和其边界表面积分的重要工具，它使得我们可以把复杂体积问题转化为边界上的面积问题，简化了计算过程。在实际应用中，需要注意函数的连续性和偏导数的存在性，以及正确识别曲面的内外侧，以确保公式适用。