1、 不可或缺的风险模型:协方差矩阵应用领域介绍 ........................... 3
1.1 组合绝对风险估计....................................................... 3
1.2 组合相对风险估计....................................................... 3
1.3 因子组合构建........................................................... 5
1.4 最大化 ICIR 因子合成.................................................... 5
2、 协方差矩阵的估计方法 .............................................. 6
2.1 样本协方差矩阵估计..................................................... 6
2.2 因子模型............................................................... 7
2.2.1 市场指数模型(单因子模型) ....................................................................................... 7
2.2.2 多因子模型 ....................................................................................................................... 8
2.2.3 统计因子模型 ................................................................................................................... 8
2.2.4 因子模型小结 ................................................................................................................... 8
2.3 压缩矩阵估计(LW 估计法) ............................................. 9
2.4 其他协方差矩阵估计方法................................................ 11
2.4.1 估计量组合 ..................................................................................................................... 11
2.4.2 GARCH+时变模型.......................................................................................................... 11
2.4.3 其他压缩方法 ................................................................................................................. 11
3、 协方差矩阵估计效果的评价方法 ...................................... 12
3.1 需要“真实协方差矩阵”的评价方法...................................... 12
3.1.1 MAD、RMSE 等统计指标............................................................................................. 12
3.1.2 组合绝对风险度量 ......................................................................................................... 12
3.1.3 基于特征距离的评价方法 ............................................................................................. 13
3.1.4 小结 ................................................................................................................................. 13
3.2 不需要“真实协方差矩阵”的评价方法 ...................................... 14
3.2.1 组合的预测波动和实际波动 ......................................................................................... 14
3.2.2 GMV 组合样本外表现.................................................................................................... 14
3.2.3 均值方差最优(MVO)组合样本外表现.................................................................... 14
4、 实证检验结果 .................................................... 15
4.1 估计方法介绍.......................................................... 15
4.2 组合未来风险预测...................................................... 15
4.3 最小风险 GMV 组合样本外表现 .......................................... 17
4.4 均值方差优化 MVO 组合样本外表现 ...................................... 18
4.5 小结.................................................................. 21
5、 总结与展望 ...................................................... 21
6、 风险提示 ........................................................ 22
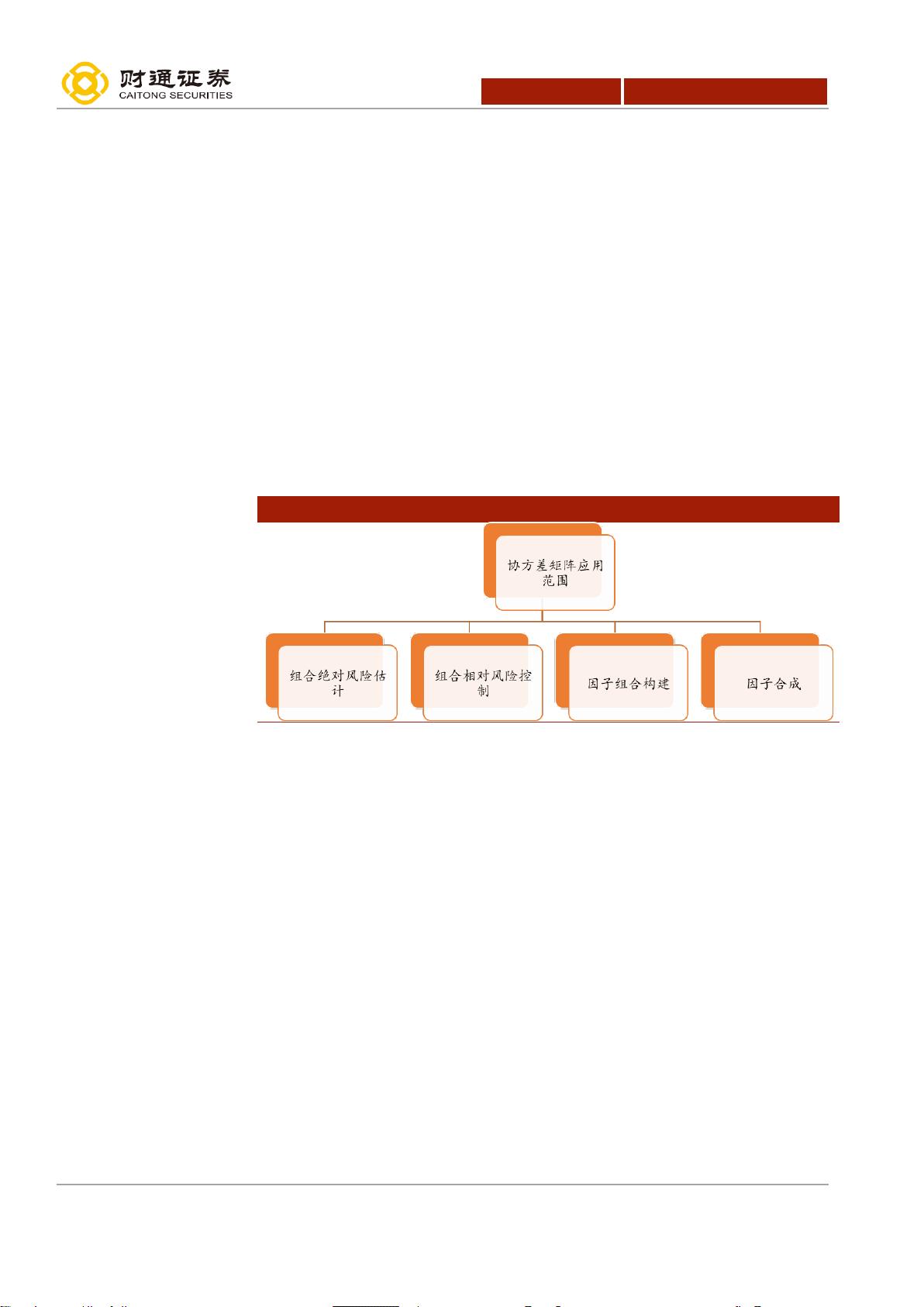
图 1:协方差矩阵应用范围 ....................................................... 3
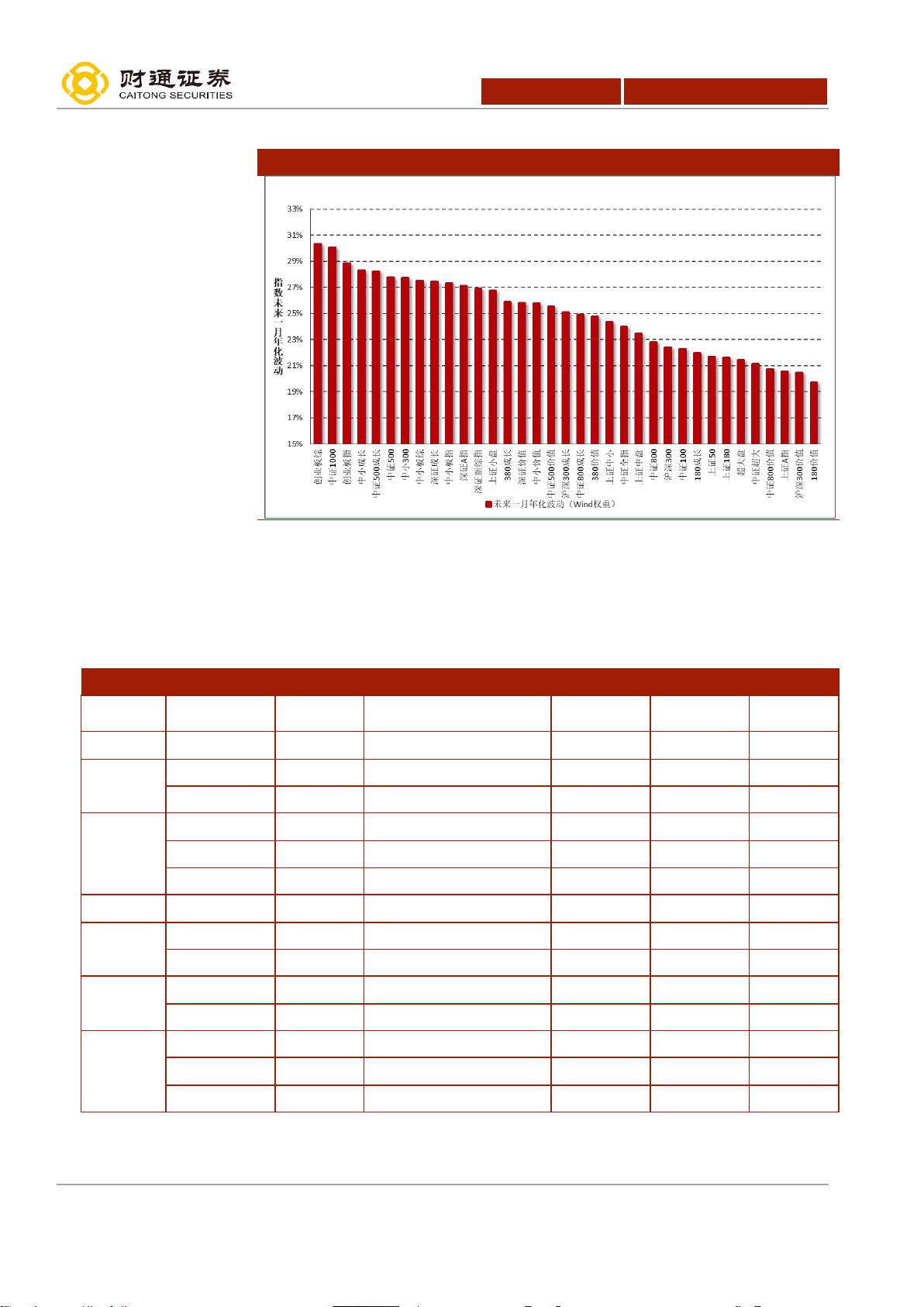
图 2:财通金工样本指数未来一个月波动预测(年化) ............................... 4
图 3:协方差矩阵估计方法汇总 ................................................... 6
图 4:压缩矩阵估计示意图 ....................................................... 9
图 5:协方差矩阵估计效果评价方法分类 .......................................... 12
图 6:Wind 全 A 指数实际风险与预测风险走势图 ................................... 16
图 7:多因子风险模型与压缩矩阵估计模型股票样本数量 ............................ 17
图 8:基准组合预期波动与 GMV 组合预期波动 .................................... 18
图 9:多因子模型风险矩阵构建的指数增强及对冲组合走势 .......................... 20
图 10:对冲组合的净值走势(行业市值中性 VS 非中性) .......................... 21
表 1:部分指数增强型基金跟踪偏离度阈值 ......................................... 4
表 2:不同协方差矩阵评价方法比较 .............................................. 15
表 3:采用的协方差矩阵估计方法 ................................................ 15
表 4:各类指数未来风险预测与实际风险相关系数(2009.12.31-2019.8.30) .......... 16
表 5:最小风险 GMV 组合样本外表现 .............................................. 17
表 6:用于组合构建的 Alpha 因子定义及基本信息 .................................. 19
表 7:指数增强对冲组合样本外表现(2010.2.26-2019.6.28) 不加行业及风格限制 .... 19
表 8:指数增强对冲组合样本外表现(2010.2.26-2019.6.28) 中性一级行业及市值中性 20