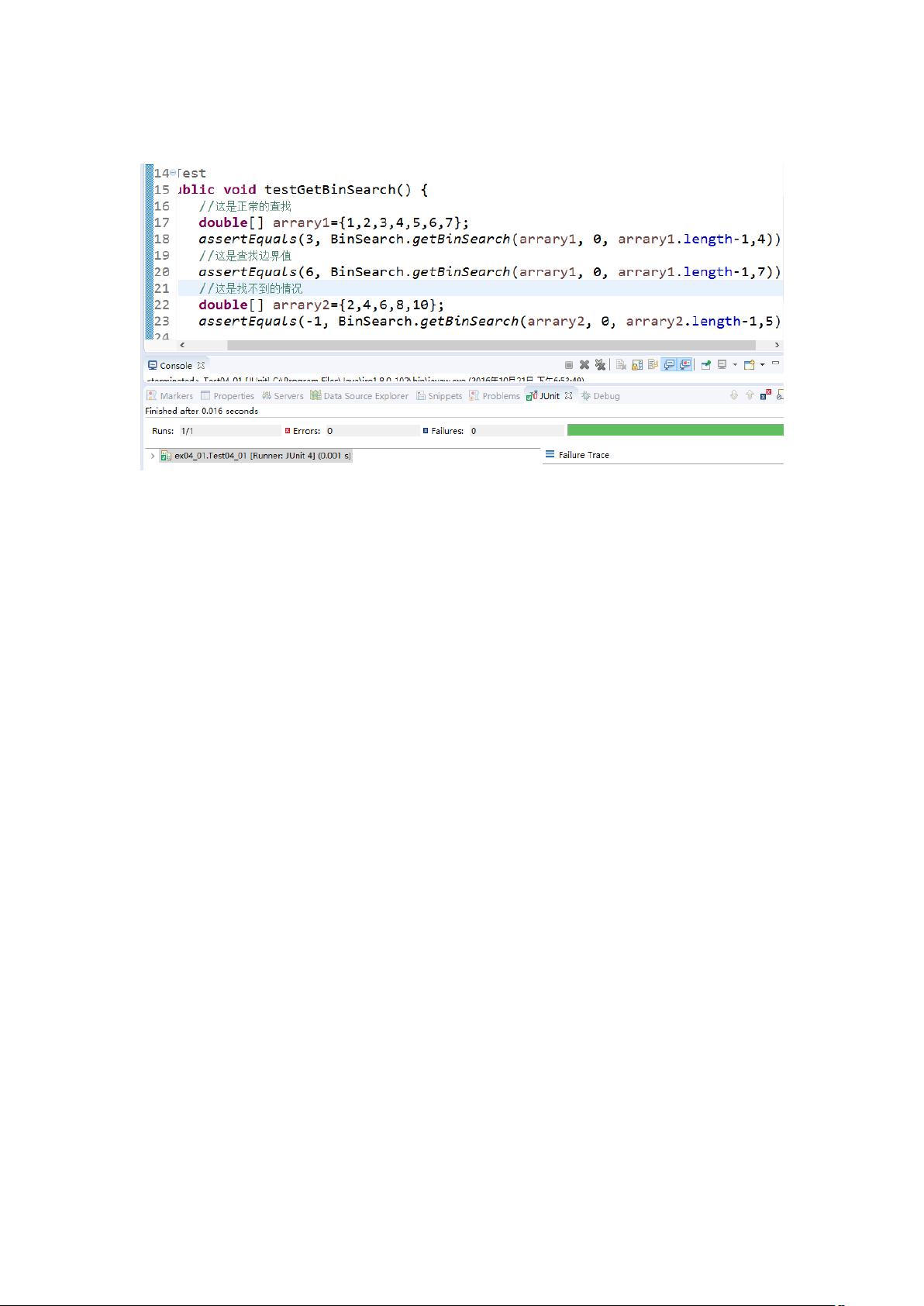
二分检索，也称为折半查找，是一种在有序数组中查找特定元素的高效算法。它的基本思想是将数组分成两半，每次比较中间元素与目标值，根据比较结果决定是在左半部分还是右半部分继续查找，直到找到目标元素或者搜索范围为空。这种算法的时间复杂度为O(log n)，比线性查找的效率更高。
在Java中，二分检索的递归实现通常会涉及以下步骤：
1. **定义递归函数**：我们需要定义一个接受数组、目标值、起始索引和结束索引作为参数的递归函数。例如，可以命名为`binarySearchRecursively`。
2. **基本情况**：递归函数需要处理两种基本情况：
- 如果起始索引大于结束索引，表示搜索范围为空，返回-1，表示未找到目标元素。
- 如果数组中间元素等于目标值，返回中间索引，表示找到了目标元素。
3. **递归情况**：如果目标值小于中间元素，对左半部分数组（起始索引到中间索引-1）调用递归函数；如果目标值大于中间元素，对右半部分数组（中间索引+1到结束索引）调用递归函数。
4. **JUnit单元测试**：为了确保代码的正确性，我们通常会使用JUnit进行单元测试。JUnit是一个用于Java的单元测试框架，它允许开发者编写断言来验证代码的预期行为。在二分检索的测试中，我们可以设置多个样例，包括目标元素在数组中、不在数组中以及在数组边界等不同情况。
5. **断言**：在JUnit测试中，断言是用来验证程序行为是否符合预期的关键部分。例如，我们可以使用`assertEquals`断言来检查二分检索的结果是否与预期相符。对于每个测试样例，我们创建一个目标值，然后调用二分检索函数并传入有序数组，最后用`assertEquals`检查返回的索引或-1（未找到）是否正确。
以下是一个简单的二分检索递归实现和相应的JUnit测试样例：
```java
public class BinarySearch {
public int binarySearchRecursively(int[] array, int target, int start, int end) {
// 递归函数实现
}
}
public class BinarySearchTest {
@Test
public void testBinarySearch() {
int[] array = {1, 2, 3, 4, 5, 6, 7, 8, 9};
assertEquals(1, binarySearchRecursively(array, 2, 0, array.length - 1)); // 成功找到
assertEquals(-1, binarySearchRecursively(array, 10, 0, array.length - 1)); // 未找到
assertEquals(4, binarySearchRecursively(array, 5, 0, array.length - 1)); // 成功找到
}
}
```
在这个例子中，我们创建了一个有序数组`array`，然后对三个不同的目标值进行测试：一个存在于数组中，一个不在数组中，另一个在数组的边界。所有样例都通过了断言，表明二分检索的递归实现是正确的。
通过这种方式，我们不仅理解了二分检索的递归实现，还了解了如何使用JUnit进行单元测试和断言来验证代码的正确性。这在软件开发中是非常重要的实践，可以确保我们的算法在实际应用中能够准确无误地工作。
