基于米勒拉宾算法的RSA密码系统_3180102927_曹逸芃1

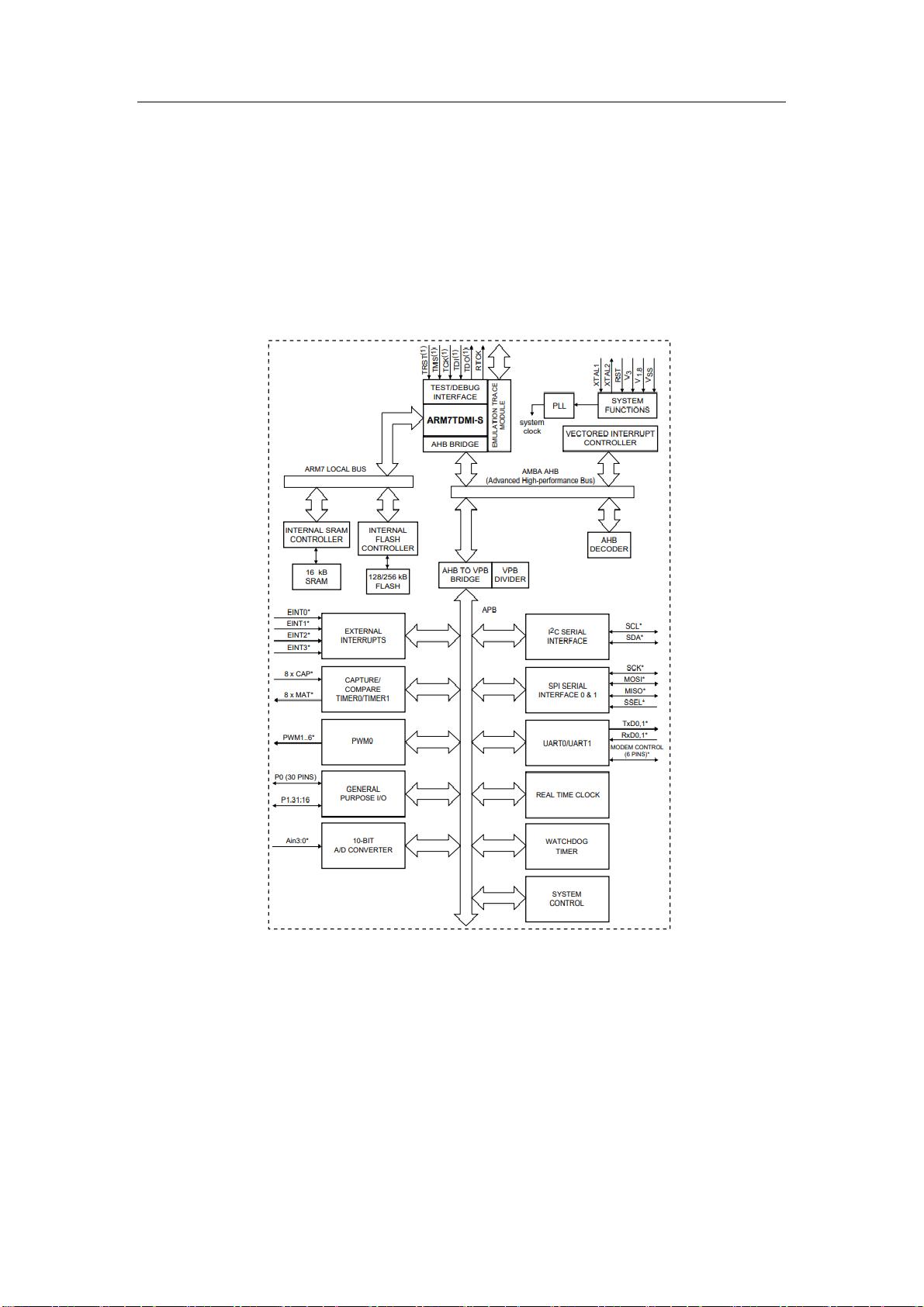
**基于米勒拉宾算法的RSA密码系统** RSA是一种非对称加密算法，它基于大数因子分解的困难性，广泛应用于网络安全领域。米勒拉宾算法则是一种用于测试大整数是否为素数的有效概率算法。在RSA系统中，米勒拉宾算法可以用于快速验证公钥的素数性质，提高加密过程的效率。 **1. 微控制器选择** 在选择微控制器时，项目选择了NXP的LPC2114型微处理器。这款微控制器基于32位ARM7TDMI-S核心，具备128KB的高速Flash存储器，支持16位Thumb模式，以减少代码大小但几乎不损失性能。LPC2114的特点还包括： - LQFP64封装，体积小巧。 - 内置SRAM和Flash存储器，支持高速操作。 - 实时仿真和跟踪功能。 - 多种外设接口，如A/D转换器、定时器、PWM输出、UART、I2C和SPI接口。 - 高达60MHz的CPU操作频率。 - 向量中断控制器和低功耗模式。 **2. 开发平台** 为了开发基于米勒拉宾算法的RSA系统，项目采用了两个主要的开发平台： - **Keil5**：这是一个完整的ARM开发工具链，包含C编译器、宏汇编、链接器、库管理器和仿真调试器。Keil5支持多种ARM内核，如ARM7、ARM9、Cortex-M系列，适合微控制器开发。其优点包括支持多种器件、丰富的例程和启动文件、用户友好的界面、大量的教程资源以及C文件编译功能，尤其适合MCU应用开发。 - **Proteus8**：这是一款电子设计自动化(EDA)工具，主要用于电路仿真。在项目中，Proteus8与Keil5配合，可以进行微控制器与外部硬件的协同仿真，验证硬件设计的正确性。 **3. 米勒拉宾算法与RSA** 米勒拉宾算法是基于伪素数测试的，它通过一系列步骤判断一个大数是否可能是素数。在RSA系统中，公钥由两个大素数p和q的乘积组成，因此在选取p和q时，可以使用米勒拉宾算法进行初步筛查，确保选取的数是素数。这样可以避免因选取合数而导致的安全性问题。 **4. RSA密码系统的实现** 实现RSA系统的关键步骤包括： - 选择两个大素数p和q，计算n=p*q，n是模数。 - 计算φ(n)=(p-1)*(q-1)，φ(n)是欧拉函数值。 - 选择一个整数e，满足1<e<φ(n)且e与φ(n)互质，e是公钥。 - 计算e的模逆数d，即存在d使得(e*d) mod φ(n) = 1，d是私钥。 - 加密过程：明文m通过公式c=m^e mod n计算得到密文c。 - 解密过程：密文c通过公式m=c^d mod n计算得到明文m。 通过在微控制器LPC2114上实现米勒拉宾算法和RSA加解密过程，可以构建一个安全的嵌入式加密系统，用于保护敏感数据的传输和存储。 总结来说，基于米勒拉宾算法的RSA密码系统利用了高效的素数检测方法，结合微控制器LPC2114的强大处理能力，以及Keil5和Proteus8开发环境的支持，实现了嵌入式环境下的安全加密解决方案。这种方法在物联网设备和嵌入式系统中有着广泛的应用前景，确保了数据在传输和存储过程中的安全性。