Introduction to Linear Algebra, 4th edition--Gilbert Strang 要点1
《线性代数入门》第四版——吉尔伯特·斯特朗的核心概念解析 线性代数是现代数学和工程学的基础,它涉及到向量、矩阵、线性方程组等多个核心概念。以下是对该书部分内容的详细解读。 1. 向量与线性组合 向量是线性代数的基本元素,它具有两个或更多分量,并在二维或三维空间中定义。向量的线性组合是指将一个向量乘以标量,然后将多个这样的结果相加。例如,在三维空间中,一个向量的线性组合可表示为cv+du+ew,其中c、d和e是标量,v、u和w是向量。向量的加法和标量乘法遵循特定规则,例如,两个向量相加等于它们的分量分别相加,而标量与向量相乘则按分量逐个乘以标量。 1. 向量长度与点积 向量的长度,也称为模,可以通过对其各分量平方后求和再开平方根得到。点积是两个向量之间的乘积,其结果是标量。若两个向量的点积为零,则它们垂直。此外,余弦公式揭示了向量之间夹角的余弦值与它们的点积和长度的关系,这在几何问题和不等式证明中非常有用。 1. 矩阵 矩阵是线性代数中的另一个关键概念,它由多个标量组成并按行和列排列。矩阵乘以向量(Ax)可以理解为矩阵的列向量对向量x的线性组合。如果矩阵A可逆,那么存在逆矩阵A-1,使得Ax=b的方程有唯一解x=A-1b。矩阵的加减操作反映了它们的效果,如差矩阵相当于逆向操作,而加矩阵则是正向操作的组合。 2. 求解线性方程组 线性方程组的求解是线性代数的核心任务。从向量的角度看,线性方程组可以通过找到适当的向量线性组合来解决。矩阵乘法的列视图强调寻找一个向量x,使得A的列向量组合成目标向量b。行视图则强调将方程组视为一系列在高维空间中的平面或超平面,解是这些平面的交点。 消元法是解决线性方程组的常用策略,它通过行变换将方程组化为上三角形式,然后通过回带法求解。消元过程中,行交换、乘以标量以及行加减都是允许的操作。无法转化为上三角形式的方程组可能无解或有无穷多解。无解的情况通常对应于行视图中的平行线,而无穷解则对应于列向量的线性相关。 通过矩阵表示消元过程,我们可以利用基础变换矩阵(如单位矩阵、消元矩阵、排列矩阵和除法矩阵)来简化计算。这些矩阵分别代表了不做任何操作、行消元、行交换和除法操作。矩阵的左乘影响行,右乘影响列,它们都从单位矩阵出发经过特定变换得到。 线性代数是理解和解决涉及向量、矩阵和线性方程组问题的基石,其理论和技巧广泛应用于物理学、工程学、计算机科学等多个领域。深入学习和掌握这些概念,对于进一步研究更高级的数学和应用问题至关重要。


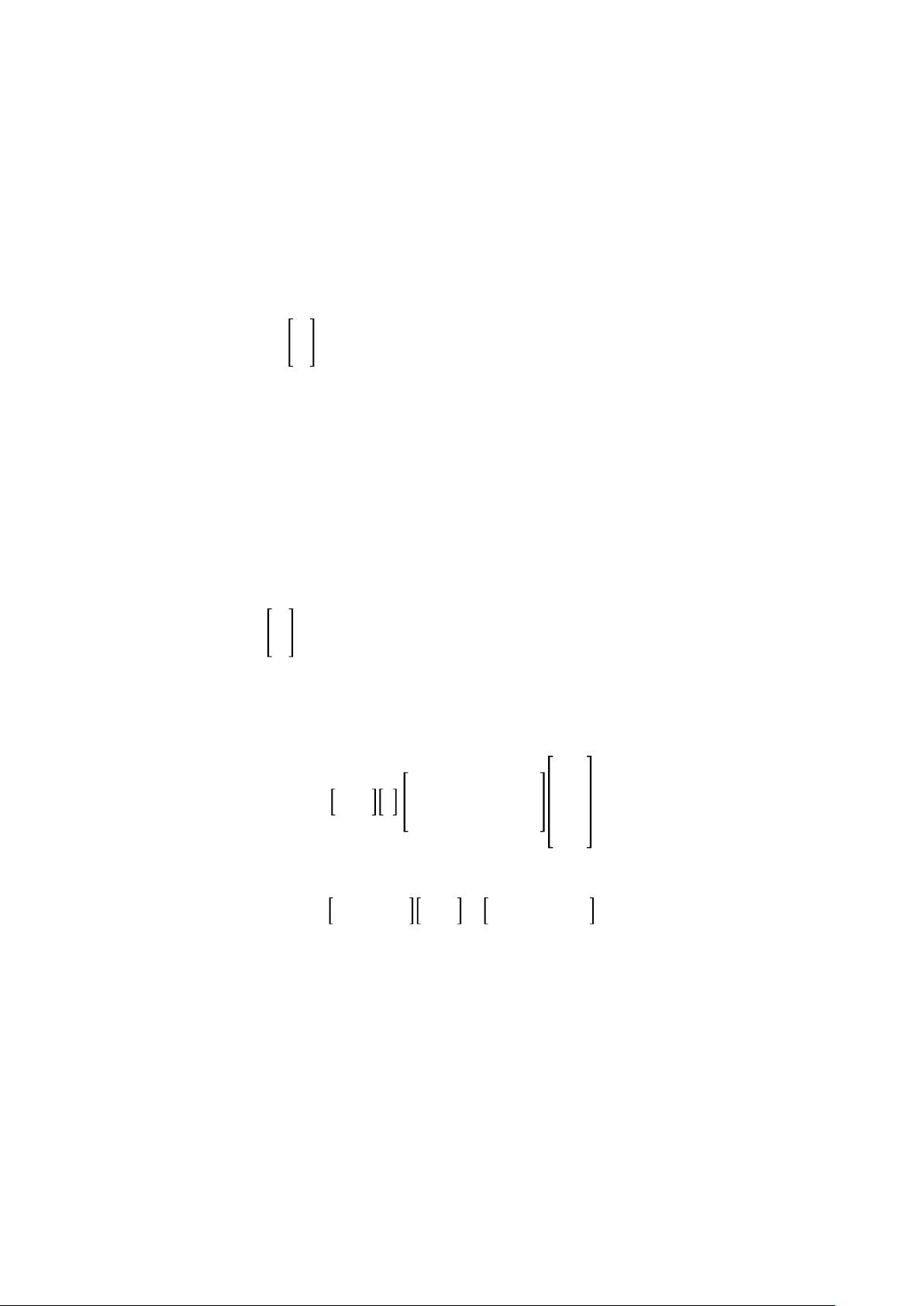
剩余19页未读,继续阅读

- 粉丝: 34
- 资源: 289
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- (源码)基于Spring Boot和MyBatis的社区问答系统.zip
- (源码)基于Spring Boot和WebSocket的人事管理系统.zip
- (源码)基于Spring Boot框架的云网页管理系统.zip
- (源码)基于Maude和深度强化学习的智能体验证系统.zip
- (源码)基于C语言的Papageno字符序列处理系统.zip
- (源码)基于Arduino的水质监测与控制系统.zip
- (源码)基于物联网的智能家居门锁系统.zip
- (源码)基于Python和FastAPI的Squint数据检索系统.zip
- (源码)基于Arduino的图片绘制系统.zip
- (源码)基于C++的ARMA53贪吃蛇游戏系统.zip


 信息提交成功
信息提交成功