Dijkstra算法图解1

Dijkstra算法是一种经典的图论算法，用于寻找图中从源节点到所有其他节点的最短路径。该算法由荷兰计算机科学家艾兹格·迪科斯彻在1956年提出，广泛应用于路由选择、网络优化等领域。在这个算法中，我们逐步构建一个最短路径树，确保每一步都扩展出当前已知的最短路径。 算法的基本步骤如下： 1. **初始化**：定义一个集合N，开始时N仅包含源节点（在例子中为节点1）。对于所有不在集合N中的节点v，设置它们的距离D(v)为无穷大（在计算机实现中通常用一个非常大的数值替代）。源节点自身的距离D(1)设置为0。 2. **寻找最小距离节点**：在N之外的节点中，选取距离D最小的节点w，并将其加入N。然后，对于所有不在N中的节点v，更新它们的距离D(v)。如果通过节点w到达节点v的路径比当前已知的路径更短，就采用这条新路径，即D(v) = min(D(v), D(w) + l(w, v))，其中l(w, v)表示节点w到v的边的权重（在这个例子中，权重即为边的长度）。 3. **重复过程**：重复步骤2，直到集合N包含了所有的节点。这意味着每个节点的最短路径已经被找到。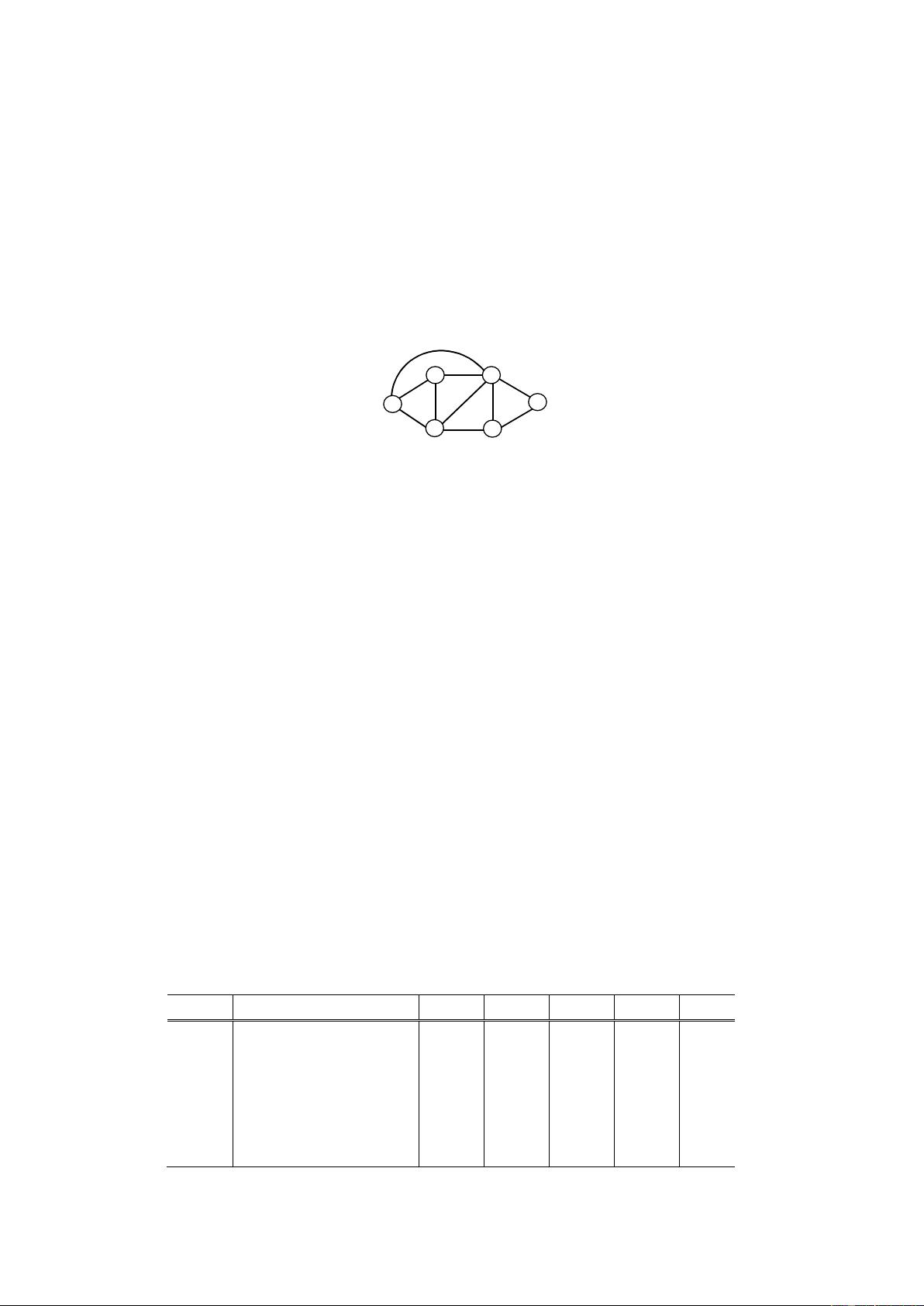 在图E-1的例子中，算法的执行过程如下： - 初始化时，N={1}，D(2)=2，D(3)=5，D(4)=1，D(5)=D(6)=∞。 - 第一步，选择D值最小的节点4加入N，更新其他节点距离，得到N={1, 4}，D(2)=2，D(3)=4，D(5)=2。 - 接下来，选择节点5加入N，更新D值，得到N={1, 4, 5}，D(3)=3。 - 然后，选择节点2加入N，更新D值，得到N={1, 2, 4, 5}，D(3)=1。 - 再次选择节点3加入N，得到N={1, 2, 3, 4, 5}，D(3)保持不变。 - 选择节点6加入N，算法结束，得到所有节点的最短路径。 这个过程确保了每次都是扩展最短的未访问路径，最终得到从源节点1到所有其他节点的最短路径树。Dijkstra算法的时间复杂度在最坏情况下为O((V+E)logV)，其中V是节点数量，E是边的数量。虽然它不能处理负权边，但在无负权边的图中，Dijkstra算法是非常高效的。