没有合适的资源?快使用搜索试试~ 我知道了~
资源详情
资源评论
资源推荐

一、图论
1.Dijkstra
1.1严格次短路计数
2.SPFA
2.1判断负环
2.2玄学优化
3.Floyd
3.1邻接矩阵快速幂
3.2传递闭包
3.3求带权无向图最小环
4.最小生成树
4.1每条边在最小生成树中的出现情况
4.2严格次小生成树
5.拓扑排序
6.差分约束
6.1区间
7.倍增求LCA
8.有向图的强联通分量
8.1有源汇DP
9.无向图的双联通分量
9.1边的双联通分量
9.2点的双联通分量
9.2.1每个点删除后剩余多少连通块
9.2.2矿场搭建
10.染色法判定二分图
11.二分图
11.1概念和性质
11.2匈牙利算法
12.网络流
12.1Dinic求最大流
12.2二分图的最大匹配
12.3无源汇上下界可行流
12.4有源汇上下界最大流
12.5最大流关建边
12.6最小路径覆盖问题
12.7最大权闭合子图
11.8最大密度子图
12.9二分图的最小权点覆盖&&最大权独立集
12.10最小费用最大流
12.11最小费用上下界可行流
12.12二分图的最大权匹配
13. 2-SAT问题
14.朱刘算法
二、数据结构
1.树状数组
2.线段树
2.1区间加/区间乘/区间求和取模
2.2区间加/区间gcd
2.3扫描线
2.4线段树维护字符串哈希
2.5三次方和
2.6线段树合并
3.树链剖分
3.1轻重链剖分
4.平衡树

4.1无旋treap
4.2链表合并
4.3维护序列
4.4静态去重的区间最大子段和
5.可持久化数据结构
5.1主席树
5.2可持久化01Trie
6.ST表
7.分块
8.莫队
8.1普通莫队
8.2带修莫队
8.3回滚莫队
8.4树上莫队
9.树套树
9.1二逼平衡树
10.整体二分
11.CDQ分治
12.Dancing Links
13.点分治
三、字符串
1.KMP
2.Trie
3.AC自动机
3.1在文中出现过的单词数量
3.2单词在文中的出现次数
3.3.计数DP
4.字符串哈希
5.循环同构串的最小表示法
6.马拉车算法
7.后缀数组
四、数学
1.筛素数
1.1线性筛
1.2埃氏筛
1.3分段筛
2.约数个数
3.约数之和
3.1 int范围求约数之和 $O(\sqrt n)$
3.2 求 $A^B$ 的约数之和
4.欧拉函数
4.1欧拉函数
4.2线性筛求欧拉函数
4.3求gcd为素数的对数
5.欧几里得算法
5.1gcd
5.2exgcd
5.3exgcd求解线性同余方程组
6.中国剩余定理
6.1中国剩余定理
6.2扩展中国剩余定理
7.高斯消元
7.1高斯消元解线性方程组
7.2高斯消元解异或线性方程组
8.求组合数
8.1杨辉三角 $O(n^2)$ 预处理
8.2 $O(n)$ 预处理阶乘
8.3卢卡斯定理

8.4高精度
8.5卡特兰数
8.6大施罗德数
9.容斥原理
10.快速幂
10.1快速幂求逆元
10.2龟速乘
11.矩阵乘法
11.1斐波那契数列前n项和
四、搜索
1.双向搜索
1.1双向BFS
1.2双向DFS
2.迭代加深
2.1加成序列
3.爆搜剪枝
3.1小猫爬山
3.2数独
3.3小木棍
3.4生日蛋糕
4.A*
4.1第k短路
4.2八数码
5.IDA*
5.1排书
5.2回转游戏
五、动态规划
1.最长上升子序列
1.1最长上升子序列
1.2拦截导弹
1.3最长公共上升子序列
2.单调队列优化DP
2.1多重背包3
2.2理想的正方形
3.状态压缩DP
3.1小国王
3.2蒙德里安的梦想
4.区间DP
4.1棋盘分割
5.树形DP
6.数位DP
6.1数位统计
6.2不降数
6.3数位之和能被n整除的数
6.4不要62
7.斜率优化DP
8.约瑟夫环
六、杂项
1.对拍
2.高精度
2.1高精度加法
2.2高精度减法
2.3高精度乘法
2.4高精度除法
3.快读
4.指令优化
5.矩阵
5.1矩阵旋转
5.2蛇形矩阵
5.3菱形前缀和
6.01分数规划
一、图论
1.Dijkstra
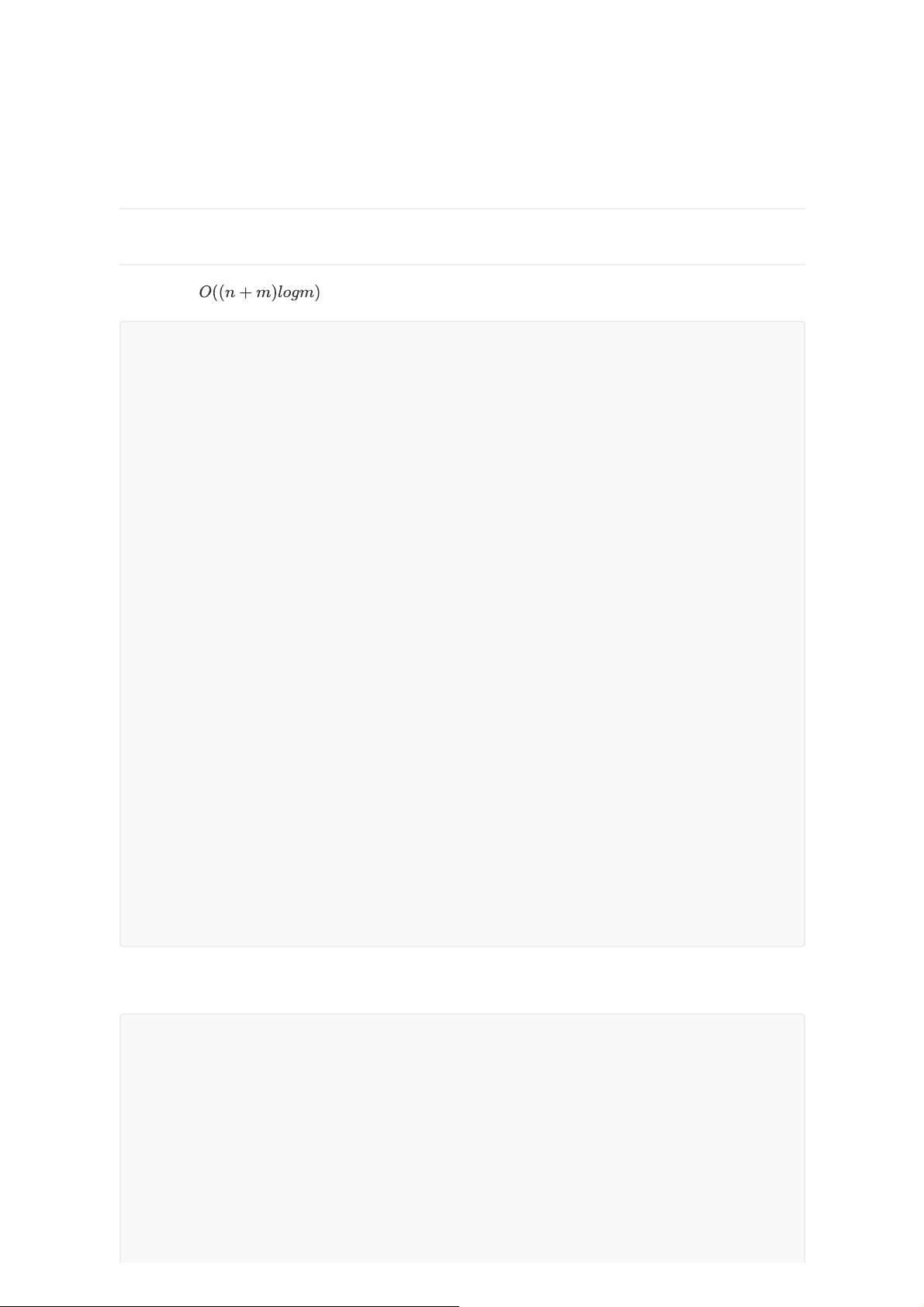
时间复杂度
1.1严格次短路计数
int d[N];
bool st[N];
void dijkstra(int root)
{
memset(st, 0, sizeof st);
memset(d, 0x3f, sizeof d);
d[root] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push((PII){0, root});
while(!heap.empty())
{
int u = heap.top().second; heap.pop();
if(st[u]) continue;
st[u] = true;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i], dist = d[u] + w[i];
if(dist < d[j])
{
d[j] = dist;
heap.push((PII){d[j], j});
}
}
}
}
int n, m, S, T;
int d[N][2], cnt[N][2]; // d[u][0]最短路, d[u][1]次短路
bool st[N][2];
int dijkstra()
{
for(int i = 1; i <= n; i ++)
d[i][0] = d[i][1] = INF, cnt[i][0] = cnt[i][1] = st[i][0] = st[i][1] =
0;
d[S][0] = 0;
cnt[S][0] = 1;
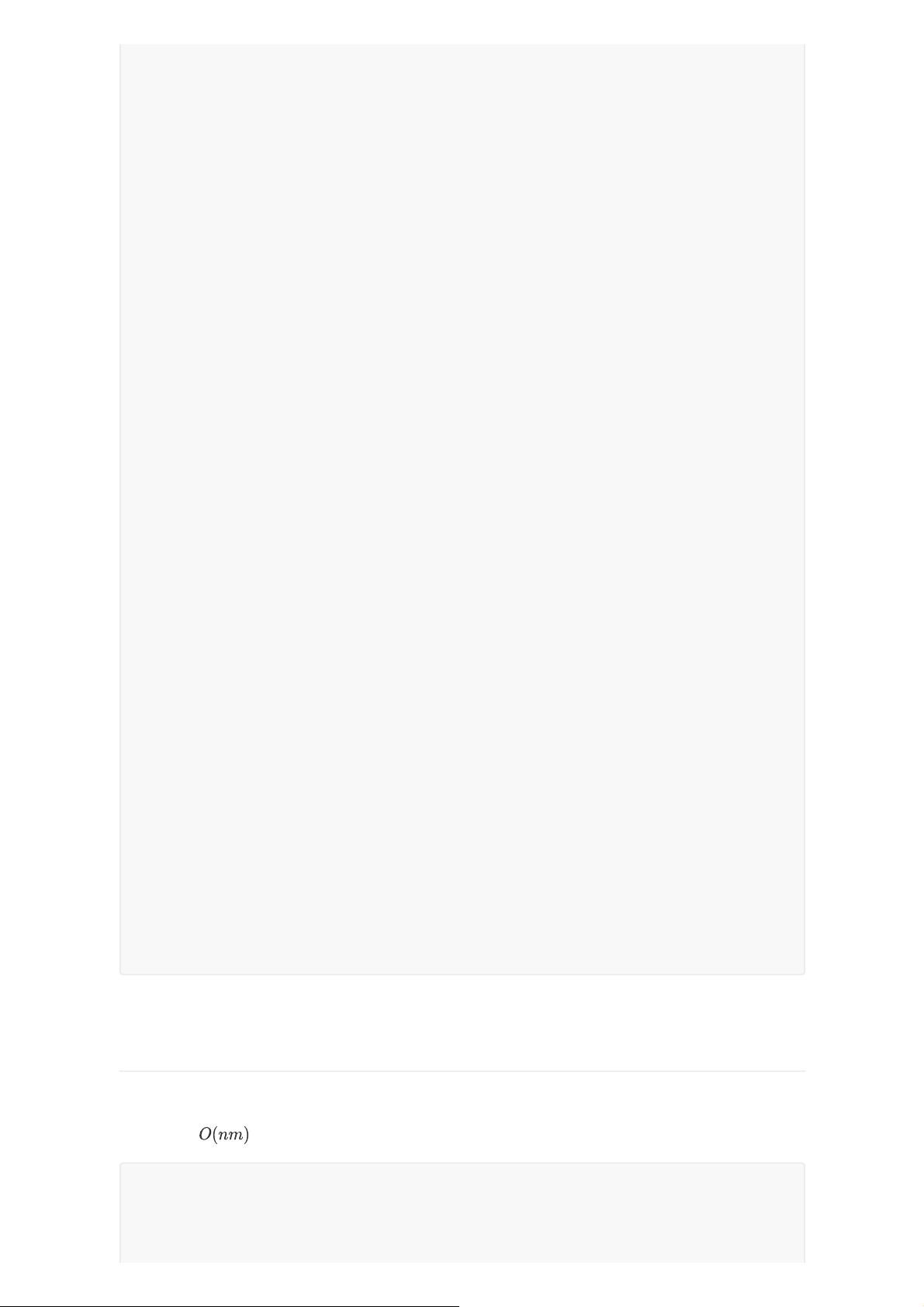
2.SPFA
手写循环队列
时间复杂度
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, S});
while(heap.size())
{
int t = heap.top().first;
int u = heap.top().second; heap.pop();
int k;
if(t == d[u][0]) k = 0;
else if(t == d[u][1]) k = 1;
else continue;
if(st[u][k]) continue;
st[u][k] = true;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i], dist = d[u][k] + w[i];
if(dist < d[j][0])
{
d[j][1] = d[j][0], cnt[j][1] = cnt[j][0];
d[j][0] = dist, cnt[j][0] = cnt[u][k];
heap.push({dist, j});
}
else if(dist == d[j][0])
{
cnt[j][0] += cnt[u][k];
}
else if(dist < d[j][1])
{
d[j][1] = dist, cnt[j][1] = cnt[u][k];
heap.push({dist, j});
}
else if(dist == d[j][1])
{
cnt[j][1] += cnt[u][k];
}
}
}
if(d[T][1] == d[T][0] + 1) cnt[T][0] += cnt[T][1];
return cnt[T][0];
}
int d[N], q[N];
bool st[N];
void spfa(int root)
{
剩余174页未读,继续阅读
神康不是狗
- 粉丝: 39
- 资源: 336
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
评论0