【免费】C余弦退火热启动1资源-CSDN文库

需积分: 0 119 浏览量 2022-08-03 14:05:48 上传评论收藏 1.47MB PDF 举报

在机器学习领域，尤其是深度神经网络（DNNs）的训练过程中，优化算法扮演着至关重要的角色。C 余弦退火（Cosine Annealing）热启动策略是一种旨在提高训练效率的技术，尤其适用于处理大型数据集时的深度学习模型。本论文在ICLR 2017会议上发表，其主要贡献是提出了一种简单而有效的随机梯度下降（Stochastic Gradient Descent, SGD）的热启动技术，用于改进训练深神经网络时的“任何时候”性能。传统的SGD优化方法中，学习率ηt通常是固定的或逐步减小的，这可能导致在训练后期收敛速度变慢，尤其是在处理高条件数函数时。为了解决这个问题，部分热启动（partial warm restarts）策略被引入到基于梯度的优化中，以提高加速梯度方案的收敛速度。C 余弦退火热启动则是在这个基础上发展出的一种新方法。该方法的核心思想是周期性地调整学习率，使其按照余弦退火曲线变化。在每个周期开始时，学习率会从一个较高的初始值开始，然后随着迭代次数增加逐渐减小，当接近周期结束时，学习率不再线性下降，而是按照余弦函数快速衰减至接近零，然后在下一个周期重新开始，即“热启动”。这种策略使得模型能够在每次周期的初期快速探索权重空间，而在后期更专注于精细调整，从而改善整体的训练效果。论文在CIFAR-10和CIFAR-100数据集上进行了实验，这两个数据集常用于评估图像分类任务的性能。通过应用C 余弦退火热启动，研究人员实现了3.14%和16.21%的分类误差率，分别刷新了这两个数据集上的最好成绩。此外，他们还在脑电图（EEG）记录数据集和ImageNet数据集的下采样版本上展示了该方法的优势。 C 余弦退火热启动的实现代码已在GitHub上公开，这为其他研究者提供了方便，使他们能够直接在自己的项目中应用这一优化策略。由于深度学习模型的训练通常需要大量计算资源，任何可以加速训练过程的方法都具有实际价值。因此，C 余弦退火热启动技术的提出，不仅在理论层面丰富了优化算法的研究，也在实践中对提升深度学习模型的训练效率做出了重大贡献。

资源详情

资源评论

资源推荐

Published as a conference paper at ICLR 2017

SGDR: STOCHASTIC GRADIENT DESCENT WITH

WARM RESTARTS

Ilya Loshchilov & Frank Hutter

University of Freiburg

Freiburg, Germany,

{ilya,fh}@cs.uni-freiburg.de

ABSTRACT

Restart techniques are common in gradient-free optimization to deal with multi-

modal functions. Partial warm restarts are also gaining popularity in gradient-

based optimization to improve the rate of convergence in accelerated gradient

schemes to deal with ill-conditioned functions. In this paper, we propose a sim-

ple warm restart technique for stochastic gradient descent to improve its anytime

performance when training deep neural networks. We empirically study its per-

formance on the CIFAR-10 and CIFAR-100 datasets, where we demonstrate new

state-of-the-art results at 3.14% and 16.21%, respectively. We also demonstrate

its advantages on a dataset of EEG recordings and on a downsampled version of

the ImageNet dataset. Our source code is available at

https://github.com/loshchil/SGDR

1 INTRODUCTION

Deep neural networks (DNNs) are currently the best-performing method for many classiﬁcation

problems, such as object recognition from images (Krizhevsky et al., 2012a; Donahue et al., 2014)

or speech recognition from audio data (Deng et al., 2013). Their training on large datasets (where

DNNs perform particularly well) is the main computational bottleneck: it often requires several

days, even on high-performance GPUs, and any speedups would be of substantial value.

The training of a DNN with n free parameters can be formulated as the problem of minimizing a

function f : IR

→ IR. The commonly used procedure to optimize f is to iteratively adjust x

∈ IR

(the parameter vector at time step t) using gradient information ∇f

) obtained on a relatively

small t-th batch of b datapoints. The Stochastic Gradient Descent (SGD) procedure then becomes

an extension of the Gradient Descent (GD) to stochastic optimization of f as follows:

t+1

= x

− η

∇f

), (1)

where η

is a learning rate. One would like to consider second-order information

t+1

= x

− η

−1

∇f

), (2)

but this is often infeasible since the computation and storage of the inverse Hessian H

−1

is in-

tractable for large n. The usual way to deal with this problem by using limited-memory quasi-

Newton methods such as L-BFGS (Liu & Nocedal, 1989) is not currently in favor in deep learning,

not the least due to (i) the stochasticity of ∇f

), (ii) ill-conditioning of f and (iii) the presence

of saddle points as a result of the hierarchical geometric structure of the parameter space (Fukumizu

& Amari, 2000). Despite some recent progress in understanding and addressing the latter problems

(Bordes et al., 2009; Dauphin et al., 2014; Choromanska et al., 2014; Dauphin et al., 2015), state-of-

the-art optimization techniques attempt to approximate the inverse Hessian in a reduced way, e.g.,

by considering only its diagonal to achieve adaptive learning rates. AdaDelta (Zeiler, 2012) and

Adam (Kingma & Ba, 2014) are notable examples of such methods.

arXiv:1608.03983v5 [cs.LG] 3 May 2017

Published as a conference paper at ICLR 2017

20 40 60 80 100 120 140 160 180 200

−4

−3

−2

−1

Epochs

Learning rate

Learning rate schedule

Default, lr=0.1

Default, lr=0.05

= 50, T

mult

= 1

= 100, T

mult

= 1

= 200, T

mult

= 1

= 1, T

mult

= 2

= 10, T

mult

= 2

Figure 1: Alternative schedule schemes of learning rate η

over batch index t: default schemes

with η

= 0.1 (blue line) and η

= 0.05 (red line) as used by Zagoruyko & Komodakis (2016);

warm restarts simulated every T

= 50 (green line), T

= 100 (black line) and T

= 200 (grey line)

epochs with η

decaying during i-th run from η

max

= 0.05 to η

min

= 0 according to eq. (5); warm

restarts starting from epoch T

= 1 (dark green line) and T

= 10 (magenta line) with doubling

mult

= 2) periods T

at every new warm restart.

Intriguingly enough, the current state-of-the-art results on CIFAR-10, CIFAR-100, SVHN, Ima-

geNet, PASCAL VOC and MS COCO datasets were obtained by Residual Neural Networks

(He et al., 2015; Huang et al., 2016c; He et al., 2016; Zagoruyko & Komodakis, 2016) trained with-

out the use of advanced methods such as AdaDelta and Adam. Instead, they simply use SGD with

momentum

t+1

= µ

− η

∇f

), (3)

t+1

= x

+ v

t+1

, (4)

where v

is a velocity vector initially set to 0, η

is a decreasing learning rate and µ

is a momentum

rate which deﬁnes the trade-off between the current and past observations of ∇f

). The main

difﬁculty in training a DNN is then associated with the scheduling of the learning rate and the

amount of L2 weight decay regularization employed. A common learning rate schedule is to use a

constant learning rate and divide it by a ﬁxed constant in (approximately) regular intervals. The blue

line in Figure 1 shows an example of such a schedule, as used by Zagoruyko & Komodakis (2016)

to obtain the state-of-the-art results on CIFAR-10, CIFAR-100 and SVHN datasets.

In this paper, we propose to periodically simulate warm restarts of SGD, where in each restart the

learning rate is initialized to some value and is scheduled to decrease. Four different instantiations

of this new learning rate schedule are visualized in Figure 1. Our empirical results suggest that SGD

with warm restarts requires 2× to 4× fewer epochs than the currently-used learning rate schedule

schemes to achieve comparable or even better results. Furthermore, combining the networks ob-

tained right before restarts in an ensemble following the approach proposed by Huang et al. (2016a)

improves our results further to 3.14% for CIFAR-10 and 16.21% for CIFAR-100. We also demon-

strate its advantages on a dataset of EEG recordings and on a downsampled version of the ImageNet

dataset.

More speciﬁcally, they employ Nesterov’s momentum (Nesterov, 1983; 2013)

Published as a conference paper at ICLR 2017

2 RELATED WORK

2.1 RESTARTS IN GRADIENT-FREE OPTIMIZATION

When optimizing multimodal functions one may want to ﬁnd all global and local optima. The

tractability of this task depends on the landscape of the function at hand and the budget of func-

tion evaluations. Gradient-free optimization approaches based on niching methods (Preuss, 2015)

usually can deal with this task by covering the search space with dynamically allocated niches of

local optimizers. However, these methods usually work only for relatively small search spaces,

e.g., n < 10, and do not scale up due to the curse of dimensionality (Preuss, 2010). Instead, the

current state-of-the-art gradient-free optimizers employ various restart mechanisms (Hansen, 2009;

Loshchilov et al., 2012). One way to deal with multimodal functions is to iteratively sample a large

number λ of candidate solutions, make a step towards better solutions and slowly shape the sampling

distribution to maximize the likelihood of successful steps to appear again (Hansen & Kern, 2004).

The larger the λ, the more global search is performed requiring more function evaluations. In order

to achieve good anytime performance, it is common to start with a small λ and increase it (e.g., by

doubling) after each restart. This approach works best on multimodal functions with a global funnel

structure and also improves the results on ill-conditioned problems where numerical issues might

lead to premature convergence when λ is small (Hansen, 2009).

2.2 RESTARTS IN GRADIENT-BASED OPTIMIZATION

Gradient-based optimization algorithms such as BFGS can also perform restarts to deal with mul-

timodal functions (Ros, 2009). In large-scale settings when the usual number of variables n is on

the order of 10

− 10

, the availability of gradient information provides a speedup of a factor of

n w.r.t. gradient-free approaches. Warm restarts are usually employed to improve the convergence

rate rather than to deal with multimodality: often it is sufﬁcient to approach any local optimum to

a given precision and in many cases the problem at hand is unimodal. Fletcher & Reeves (1964)

proposed to ﬂesh the history of conjugate gradient method every n or (n + 1) iterations. Powell

(1977) proposed to check whether enough orthogonality between ∇f (x

t−1

) and ∇f (x

) has been

lost to warrant another warm restart. Recently, O’Donoghue & Candes (2012) noted that the iterates

of accelerated gradient schemes proposed by Nesterov (1983; 2013) exhibit a periodic behavior if

momentum is overused. The period of the oscillations is proportional to the square root of the local

condition number of the (smooth convex) objective function. The authors showed that ﬁxed warm

restarts of the algorithm with a period proportional to the conditional number achieves the optimal

linear convergence rate of the original accelerated gradient scheme. Since the condition number is

an unknown parameter and its value may vary during the search, they proposed two adaptive warm

restart techniques (O’Donoghue & Candes, 2012):

• The function scheme restarts whenever the objective function increases.

• The gradient scheme restarts whenever the angle between the momentum term and the

negative gradient is obtuse, i.e, when the momentum seems to be taking us in a bad direc-

tion, as measured by the negative gradient at that point. This scheme resembles the one of

Powell (1977) for the conjugate gradient method.

O’Donoghue & Candes (2012) showed (and it was conﬁrmed in a set of follow-up works) that these

simple schemes provide an acceleration on smooth functions and can be adjusted to accelerate state-

of-the-art methods such as FISTA on nonsmooth functions.

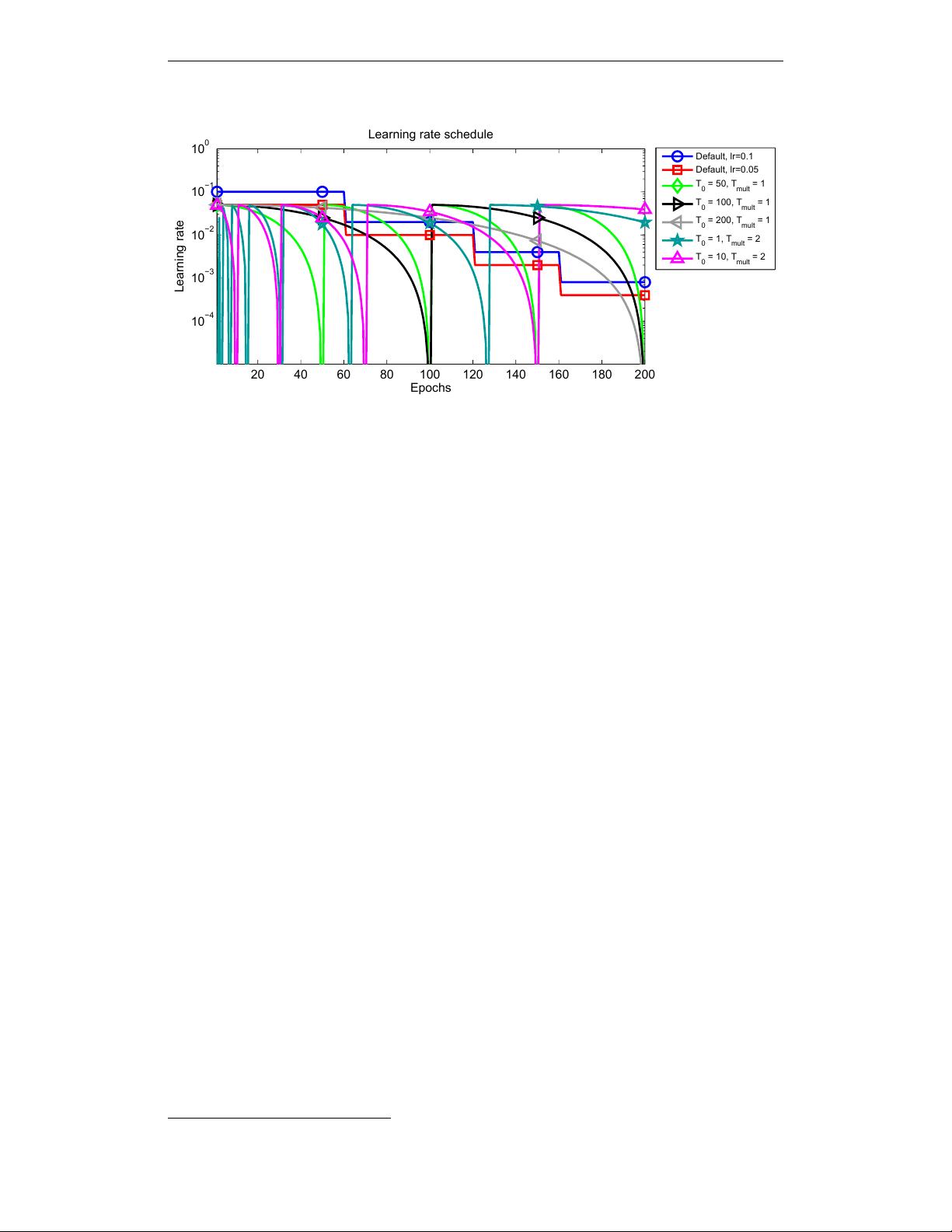
Smith (2015; 2016) recently introduced cyclical learning rates for deep learning, his approach is

closely-related to our approach in its spirit and formulation but does not focus on restarts.

Yang & Lin (2015) showed that Stochastic subGradient Descent with restarts can achieve a linear

convergence rate for a class of non-smooth and non-strongly convex optimization problems where

the epigraph of the objective function is a polyhedron. In contrast to our work, they never increase

the learning rate to perform restarts but decrease it geometrically at each epoch. To perform restarts,

they periodically reset the current solution to the averaged solution from the previous epoch.

剩余15页未读，继续阅读

评论收藏

内容反馈

赶路的稻草人

粉丝: 32
资源: 330

C 余弦退火热启动1

评论0

最新资源

C 余弦退火热启动1

评论0

c语言编写的余弦曲线

升余弦滤波器和根升余弦滤波器

有趣简单必学基础的C语言控制台案例-输出正余弦函数，直线，圆图像

C语言绘制余弦、正弦曲线

C语言正余弦函数分段查表计算器

离散余弦变换以及c代码

正余弦函数曲线的C语言绘制方法

C语言：使用函数求余弦函数的近似值

余弦相似度算法实现

根升余弦滤波器.rar_升余弦_成型滤波_根生余弦频域_频域成型_频域滤波器

余弦相似度算法(python代码)

2.9.5 余弦相似度-明鉴1

余弦定理求第三边.cpp

余弦相似度算法计算方法

余弦相似度计算代码

Java基于余弦方法实现的计算相似度算法示例

浅谈正余弦编码器及细分

离散余弦变换原理和JPEG压缩算法

升余弦滤波器.docx

升余弦信号的时域波形

MATLAB升余弦滤波器

余弦相似度MATLAB代码

余弦曲线的图像

升余弦滚降系统,升余弦滚降系统结论

机器学习-余弦相似度计算图片相似性

余弦相似度

升余弦滚降滤波程序MatLAB

MATLAB 升余弦 滚降系统 设计

最新资源

MATLAB 升余弦滚降系统设计