31-图算法-单源最短路径-BellmanFord1

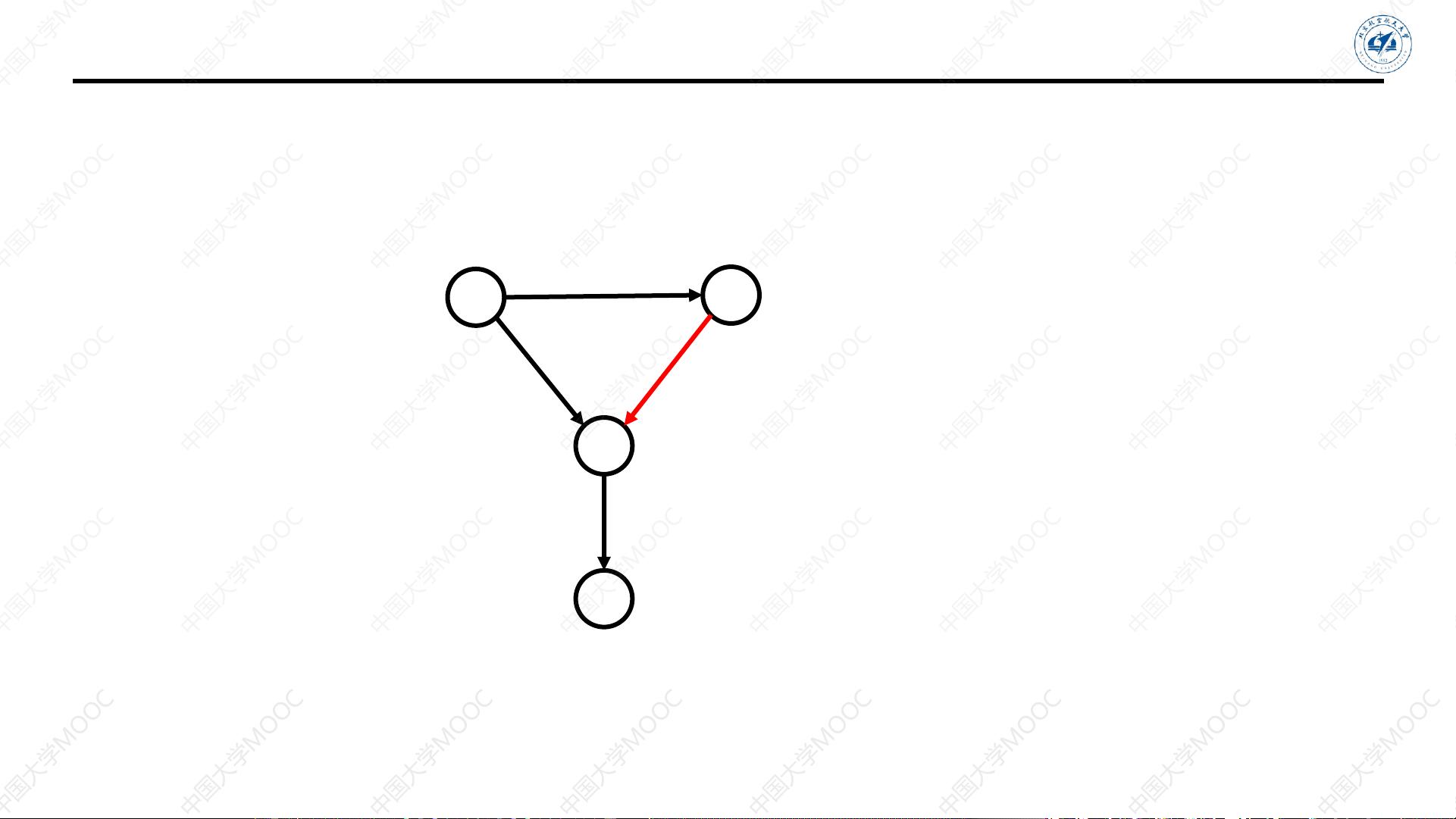
【正文】 在图算法的研究中，单源最短路径问题是一个重要的议题，它涉及到寻找从图中的一个特定顶点（源点）到其他所有顶点的最短路径。在这个问题中，"31-图算法-单源最短路径-BellmanFord1" 提到了一种解决方案——贝尔曼-福特（Bellman-Ford）算法。该算法是由理查德·贝尔曼在1958年提出的，它可以处理带有负权边的图，这是它与Dijkstra算法的一个显著区别。 **问题背景** 在实际应用中，图模型常用于表示各种网络结构，如道路网络、计算机网络、社交网络等。在这些网络中，我们可能需要找出从某个起点出发，到达其他所有点的最短路径。例如，在道路网络中，我们可能想知道从一个城市出发到其他所有城市的最短驾驶路线；在网络路由中，我们希望找到数据包从源头到目的地的最小跳数路径。然而，如果边的权重可以为负，如表示优惠或费用减免，那么Dijkstra算法就不再适用，因为其假设边的权重非负。此时，贝尔曼-福特算法就能派上用场。 **算法思想** 贝尔曼-福特算法的核心思想是松弛操作（relaxation），即通过不断更新顶点间的距离来逐步逼近最短路径。算法初始时，将源点到自身的距离设为0，其他所有顶点的距离设为无穷大。然后进行V-1轮迭代，每轮迭代中遍历所有边，如果发现一条边可以缩短某个顶点的最短路径，就进行更新。如果在V-1轮迭代后仍然有边可以缩短路径，说明存在负权环，这是算法的一个重要特性，因为在有向图中，负权环会导致路径长度无限减小。 **算法实例** 以一个简单的有向图为例，假设源点是A，图中有边(A,B)：-3，(B,C)：2，(C,A)：-4。初始时，A到A的距离是0，到B和C的距离是无穷大。第一轮迭代中，发现(A,B)可以缩短A到B的距离，更新为-3；接着(B,C)缩短了A到C的距离，更新为1。第二轮迭代，(C,A)使得A到C的距离缩短，更新为-1。由于没有负权环，所以经过两轮迭代，所有顶点的最短路径已经找到。 **算法分析** 贝尔曼-福特算法的时间复杂度是O(V*E)，其中V是顶点的数量，E是边的数量。虽然比Dijkstra算法的O(E+V*logV)要慢，但它的优势在于能够处理含有负权边的情况。然而，如果图中确实不存在负权边，Dijkstra算法通常会更快。 **算法性质** 1. **负权边处理**：贝尔曼-福特算法能够正确处理图中存在负权边的情况，包括识别负权环。 2. **V-1轮迭代**：算法需要进行V-1轮迭代才能确保找到最短路径，除非在某轮迭代中发现负权环。 3. **正确性**：每次松弛操作都确保了当前路径是最短的，因此在没有负权环的情况下，最终得到的结果一定是全局最短路径。 4. **检测负权环**：如果在V-1轮迭代后仍然存在边可以缩短路径，说明图中存在负权环。 **应用场景** 贝尔曼-福特算法广泛应用于需要考虑负权重的场景，如交通网络分析、金融交易系统中的成本计算，以及路由协议中处理带宽限制和优先级的场景。 总结起来，贝尔曼-福特算法是解决单源最短路径问题的一种重要方法，尤其适用于包含负权边的图。尽管其时间复杂度相对较高，但其对负权边和负权环的处理能力使其在特定领域具有不可替代的价值。在学习和应用图算法时，理解和掌握贝尔曼-福特算法是非常关键的。