1. Pinhole Model
1.1. 针孔模型简介
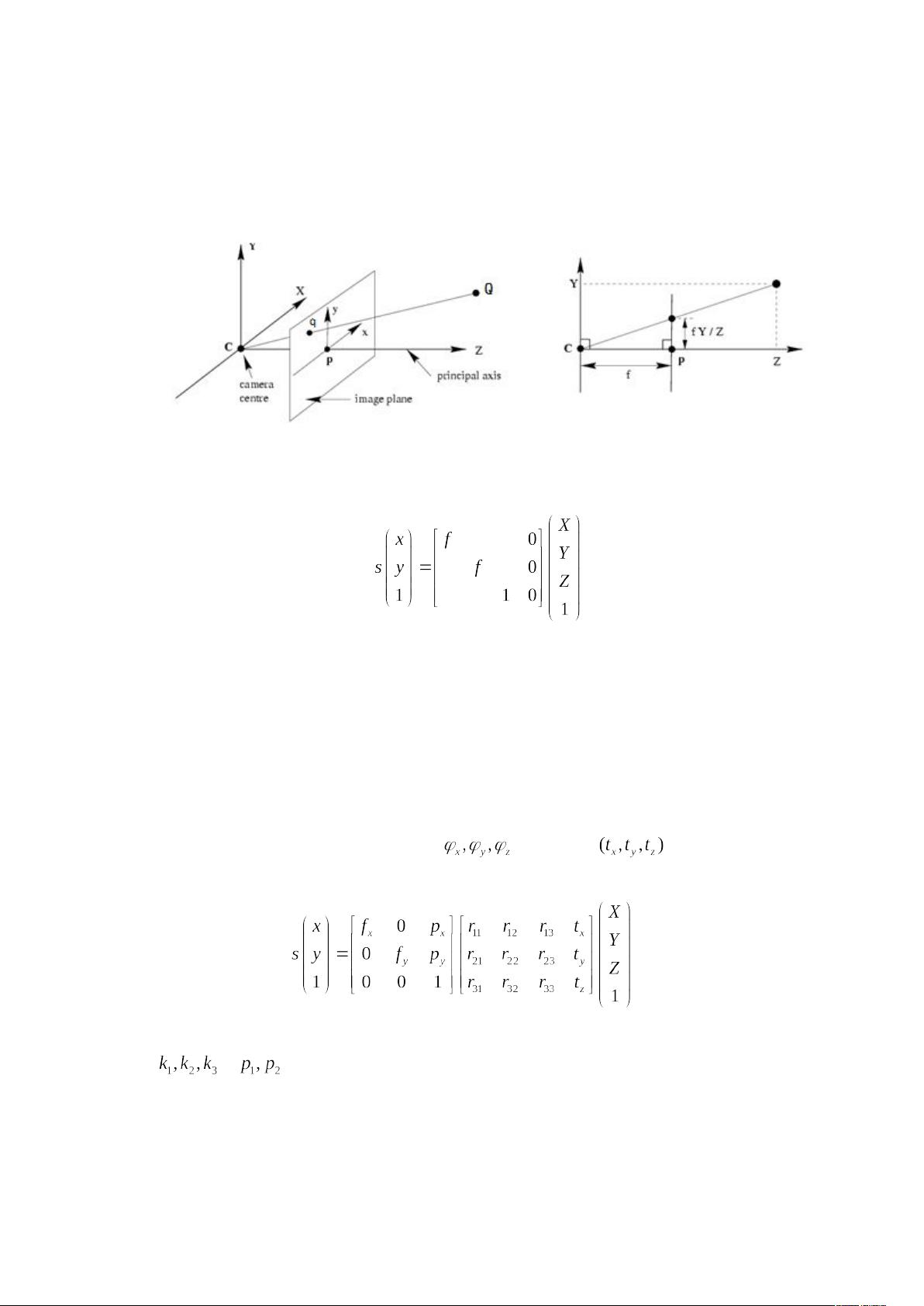
针孔模型是摄像机模型中较为简单的一种。它有一种等价形式,也就是把成像表面放
到针孔前面,如下图所示。
点 Q(X,Y,Z) 由通过投影中心的光线投影到图像平面上,对应的点为 q(x,y,z)。由相似三
角形的定理,得到 Q 和 q 的如下关系:(x,y) = (fX/Z, fY/Z),其中 f 是摄像机的焦距。为了使
表达式线性,采用齐次坐标表达:
1.2. 摄像机参数
在利用摄像机进行任何任务之前,获得摄像机拍摄到的图像与实际景物之间的关系都
是重要的。为此需要在针孔模型的基础上建立一个能够描述摄像机特性的模型。首先,由
于制造上的误差,投影中心在图像平面上的对应点 P 不一定在图像中心,设其为(px,py)。
其次,点 q 的单位是像素,而 Q 的单位是米,因此 f 的单位是像素/m。而我们不能保证感
光器件上像素是正方形的,这就是说 x 方向和 y 方向上的 f 可能不一样,设其分别为 fx,
fy。以上参数称为摄像机的内参数。
当景物不动、摄像机旋转或平移时,或者相反时,景物坐标还需要乘以一个旋转 /平移
矩阵才能够进行下一步运算。旋转的角度 和平移向量 称为摄像机的外
参数。因此我们有
[1]
:
实际的透镜往往会有少量畸变,影响较大的畸变有径向畸变和切向畸变,可分别用参
数 和 表示。具体的表达式可见[2]。
2. Camera Calibration
2.1. 概述
我们假定无法拆开相机观察其参数,只能通过图像标定来计算。微软研究院的张正友



















- 1
- 2
前往页