ch06 动态规划（二）.pdf

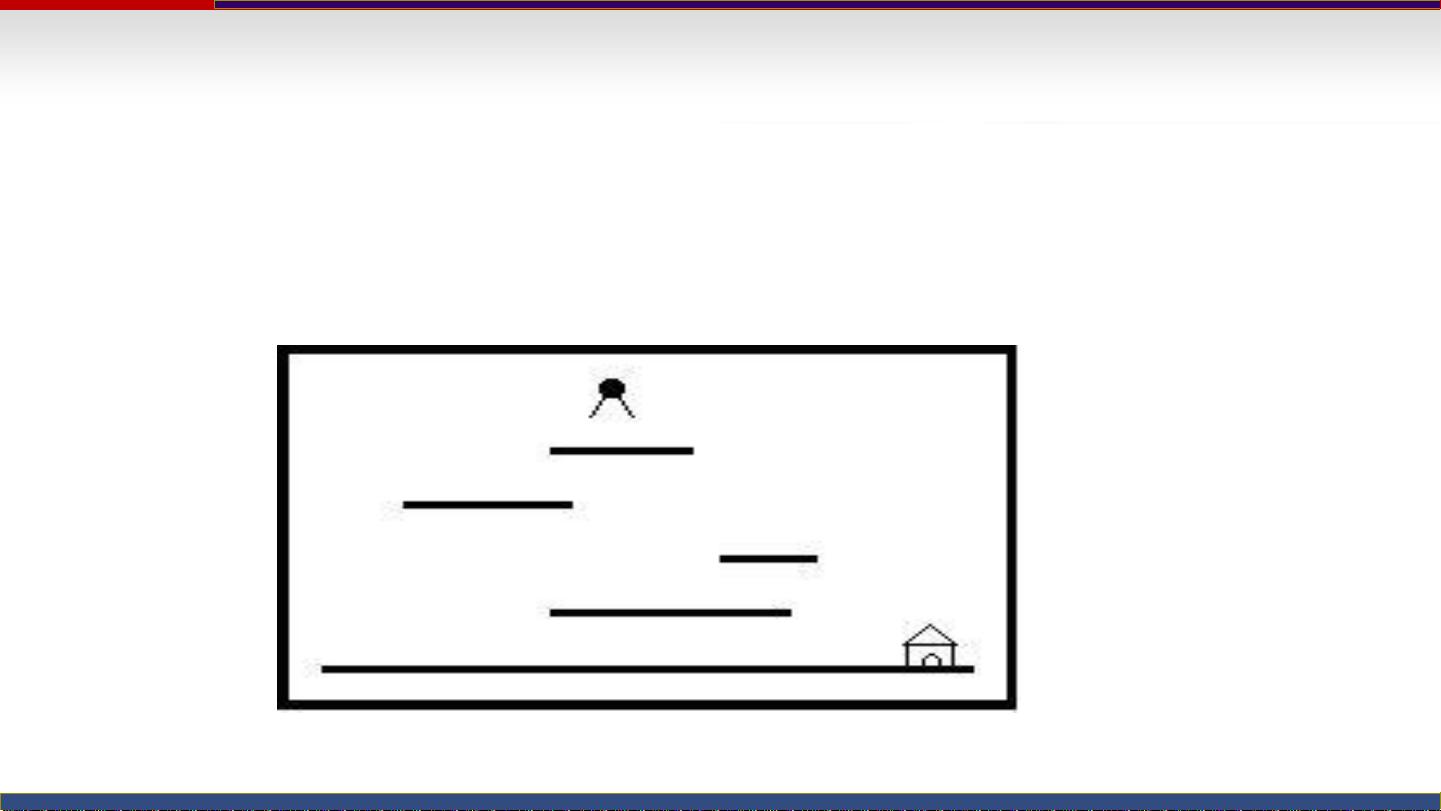
从提供的文件内容来看，知识点主要围绕动态规划算法在解决特定问题上的应用。文件中详细描述了两个案例：“HelpJimmy”游戏和“神奇的口袋”问题，并提出了相应的算法实现思路。 ### HelpJimmy游戏 #### 问题描述： HelpJimmy游戏的目标是计算Jimmy老鼠从某一高度下落到地面的最短时间。在这个游戏场景中，存在多个长度和高度不同的平台，Jimmy每次下落的高度不能超过一个预设的最大值，否则游戏结束。游戏者需要决定在Jimmy落到每个平台上时，向左还是向右跑动。 #### 解题思路： 动态规划在这里被用来求解如何通过平台到达地面的最短时间。具体方法是将问题分解成两个子问题：从平台左端到地面的最短时间和从平台右端到地面的最短时间。通过构建函数LeftMinTime(k)和RightMinTime(k)来分别代表这两个子问题的解，并通过递归关系式来逐步求解。最后求解LeftMinTime(0)即可得到Jimmy从起始位置到达地面的最短时间。 #### 时间复杂度分析： 算法的时间复杂度为O(n^2)，因为每个平台的左右两端最小时间的计算都需要遍历所有平台一次，总共有n个平台。 ### 神奇的口袋问题 #### 问题描述： 有一个神奇的口袋，其容积为40。John有一系列物品，每个物品的体积不同，介于1到40之间。John需要挑选出一些物品，使得这些物品的总体积正好等于40。需要计算出John能够以多少种不同的方式做到这一点。 #### 解题思路： 这个问题可以通过组合数学中的组合问题来解决。可以使用一个数组dp来记录每个体积下能达到的方式数。初始化dp[0]为1，表示体积为0的情况下总是有一种方式（即不取任何物品）。对于每个物品，更新dp数组，即遍历所有可能的体积，加上当前物品的体积后的状态，更新为之前状态加上当前物品的值。最终，dp[40]即为所求解。 #### 时间复杂度分析： 使用动态规划解决问题的时间复杂度为O(n)，其中n是物品的数量。因为每添加一个物品，只更新dp数组中的一个元素，所以总的操作次数与物品数量线性相关。 ### 总结 上述内容涉及的动态规划知识点包括： 1. 动态规划的基本原理：将复杂问题分解为子问题，并构建状态转移方程求解。 2. 通过递归关系式的构建来求解问题，正确使用边界条件（如Jimmy游戏的LeftMinTime(0)）。 3. 状态数组的构建与初始化，确保动态规划过程能正确运行。 4. 动态规划的时间复杂度分析，包括子问题数量和每个子问题解决所需时间的计算。 5. 组合问题的解决方法，使用动态规划来计数，以及如何更新状态转移方程。 6. 不同类型的问题如何使用动态规划进行建模和求解。 通过这两个案例，我们不仅学习到了动态规划算法在解决实际问题中的应用，还了解了如何通过动态规划来优化问题求解的时间复杂度。