没有合适的资源?快使用搜索试试~ 我知道了~
基于非线性时间序列分析经验模态分解和小波分解异同性的研究.pdf
需积分: 18 1 下载量 96 浏览量
2020-06-30
16:37:32
上传
评论
收藏 521KB PDF 举报
温馨提示
据龚志强等人的研究认为:(1)EMD方法是波动上、下包络的平均值去确定“瞬时平衡位置”,进而分解IMF分量;WD方法是带通滤波器,分解得到的各个细节分量一般与固定频带相对应,故分解的结果不及EMD精确,但WD方法能够解决EMD各个IMF分量的正交性较差问题。因此,可以将EMD和WD方法结合,更加有效地识别数据的特征信息。(2)EMD方法,既适用于线性序列分析,又适用于非线性序列分析;WD方法对线性序列的分析效果较好,对非线性序列的效果一般,尤其是对高频的分辨率较差,其小波系数方差可能会掩盖一些高频的周期。
资源推荐
资源详情
资源评论

基于非线性时间序列分析经验模态分解和
小波分解异同性的研究
!
龚志强
!
)
"
)
邹明玮
!
)
#
)
高新全
"
)
董文杰
"
)
!
)
(扬州大学物理科学与技术学院,扬州
""$%%&
)
"
)
(国家气候中心气候研究开放实验室,北京
!%%%’!
)
#
)
(中国科学院大气物理研究所,北京
!%%%"&
)
(
"%%(
年
!"
月
#
日收到;
"%%$
年
"
月
"!
日收到修改稿)
基于经验模态分解(
)*+
)的希尔伯特变换(
,-
),是对非线性时间序列基于
)*+
进行分解,然后通过
,-
获得
频谱
.
利用理想时间序列和青藏高原古里雅冰芯
!’
/
时间序列,系统地分析比较了
)*+
和小波分解(
0+
)以及
,-
和
小波变换在非线性时间序列处理中的优劣,并针对它们各自的缺点提出了可能改进的设想
.
研究结果表明,将基于
)*+
的方法和基于
0+
的方法有机结合起来应用,可以更有效地识别原时间序列的特征信息
.
关键词:经验模态分解,小波分解,理想时间序列,古里雅冰芯
!"##
:
&"1%2
!
国家重点基础研究发展规划(批准号:
"%%(34(!’#%%
)和国家自然科学基金(批准号:
&%(!!%%’
,
(%"#!%%1
)资助的课题
.
!5
引 言
!&&’
年
,6789
提出希尔伯特
:
黄变换(
,,-
)
[
!
]
,
随后又对其进行了改进
[
"
]
. ,,-
本质上是对一个信
号(或其导数,视所需的分解精度而定)进行平稳化
处理,其结果是可以把不同特征尺度或层次的波动
或趋势从原信号中分解出来,得到一系列具有不同
特征尺度的本征模函数(
;*<
)分量,然后各个分量
经希尔伯特变换(
,-
)得到希尔伯特谱
.
该方法被认
为是近年来以傅里叶变换为基础的线性和稳态谱分
析的一个重大突破
.
小波变换(
0-
)是泛函分析、傅里叶变换、样条
分析、调和分析、数值分析的完美结晶,其在时频域
中具有良好的局部化特征,能够比较有效地从变化
的信号中提取突变信息,通过对基函数的伸缩、平移
运算,达到对信号的多分辨率分析
[
#
—
1
]
.
本文利用基
于经验模态分解(
)*+
)和基于小波分解(
0+
)的分
析方法
[
=
,
’
]
对由正弦函数和余弦函数构建的理想时
间序列
!
(
"
)(
!%
个周期,每个 周期
!%%
点,共计
!%%%
点)和青藏高原古里雅冰芯
!’
/
时间序列
#
!’
/
(公元
#%!
—
!&&%
年)资料进行分析处理,系统地比
较了两种方法的优劣,并针对它们各自的缺点提出
了可能改进的设想
.
"5
理想时间序列的构建和分析
理想时间序列为
!
(
"
)
>
#?@8
(
"
!
A
%." "
)
B
CD?
(
"
!
A
%.’ "
)
.
(
!
)
该时间序列由频率为
%5" ,E
的正弦函数和
%5’ ,E
的余弦函数叠加而成,原序列以
%5" ,E
为基频,采
集
!%
个周期,每个周期
!%%
点,共计
!%%%
点(见
图
!
)
.
图
"
为
!
(
"
)基于
)*+
的
;*<
分量的时域图
.
;*<!
是从原序列中分解出的振幅
$
最小、频率
%
最
高的
;*<
分量,各
;*<
分量的振幅依次逐渐增大、
频率逐渐降低,直到频率很低的
;*<1. ;*<=
的振幅
明显比
;*<1
的振幅大,这种异常是
)*+
中经常会
出现的情况,但只可能出现在较低频的部分,不会影
响整体的变化趋势
. ;*<
分量的这种分布状况是由
其本身的特性决定的,
)*+
总是把最主要的信息先
提取出来,即最先由
)*+
方法分解出的几个
;*<
分
量,包含了原序列最主要的信息,所以
)*+
方法也
是一种新的主成分分析法
[
!
,
&
]
.
图
"
中
;*<!
,
;*<"
即
为原序列最主要的
;*<
分量
. ;*<!
频率最高,振幅
较小,对应原序列
%5’ ,E
的余弦部分;
;*<"
频率略
第
$(
卷 第
’
期
"%%$
年
’
月
!%%%:#"&%F"%%$F$(
(
%’
)
F#&(=:!!
物 理 学 报
G3-G H,IJ;3G J;K;3G
LDM.$(
,
KD. ’
,
G696?N
,
"%%$
"
"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
"%%$ 3O@8. HOP?. JDC.
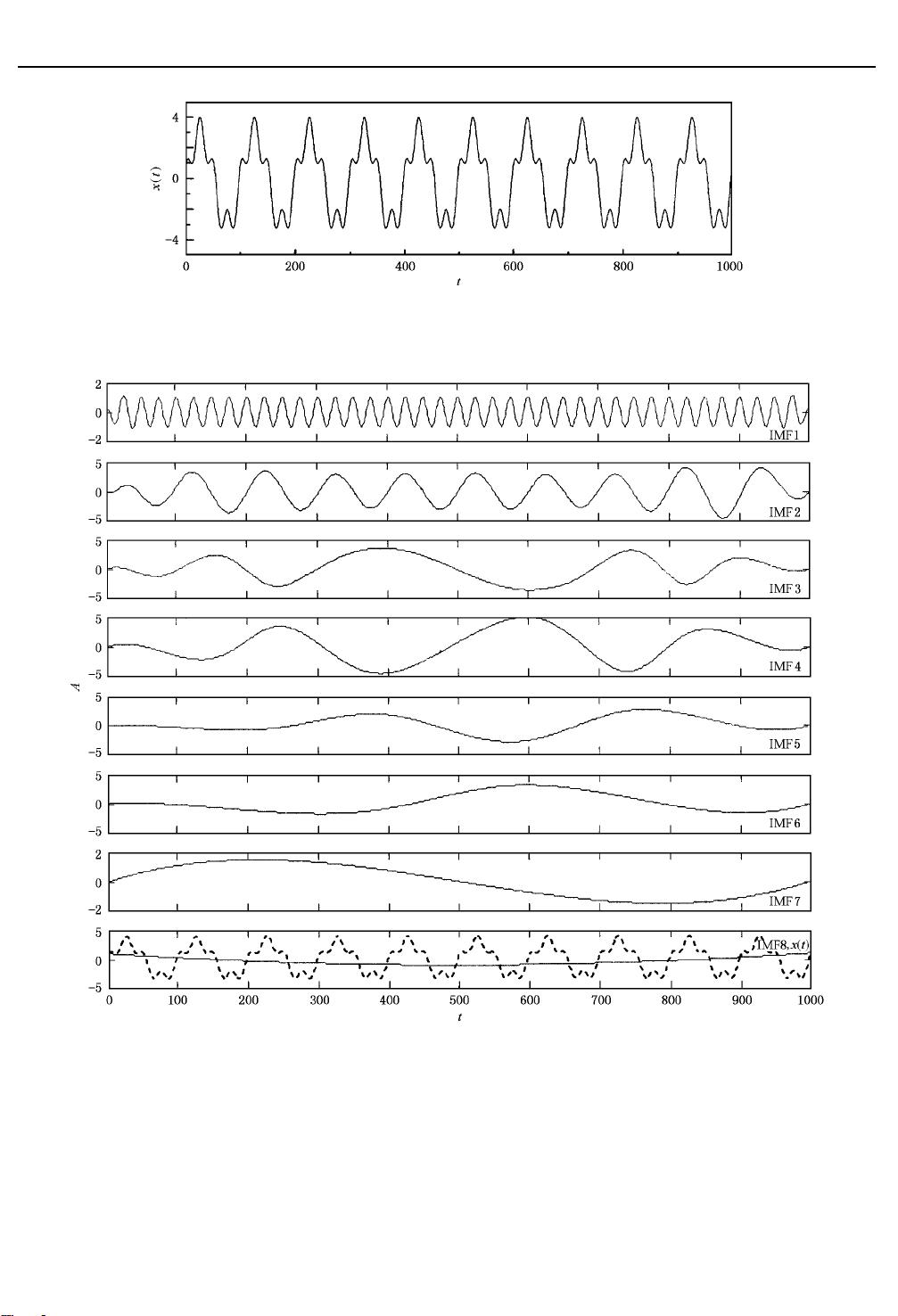
图
!
理想时间序列
图
" !
(
"
)基于
#$%
的
&$’
分量的时域图
&$’!
—
&$’(
依次为
#$%
的
(
个
&$’
分量
) &$’(
,
!
(
"
)中实线为
&$’(
,虚线为
!
(
"
)
低于
&$’!
,振幅较大,对应原序列
* + " ,-
的正弦部
分
) &$’"
的振幅和频率有微小的波动,主要原因是
在分解中采用了
.
次样条拟合近似,分解得到的分
量并不是真正的原序列波形,但这些小的波动不会
影响对原序列总体性质的分析
) &$’(
是一个近似单
调变化的序列,表征原序列的整体趋势,即平常所说
的线性趋势项,它具有非常明确的物理含义
)
图
.
为
!
(
"
)基于
/%
的细节分量和近似分量
的时域图
)
小波基函数采用
%012345637
小波,重构滤
波器的阶数为
8
,分解滤波器的阶数为
9 ) %!
—
%.
这
.
层细节分量所包含的信息,无论是频率还是振幅
都不能体现原序列的特点,故
/%
并不是将最主要
的分量最先提取出来,相反,最初的细节分量往往包
含了干扰和噪声等一些无用的信息,所以这
.
个分
(:9.
物 理 学 报
8:
卷
剩余10页未读,继续阅读
资源评论

青溪
- 粉丝: 0
- 资源: 3
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- C# winform -类火车头采集器、采集工具、任务新建和编辑、网址采集、 标签编辑、数据采集、数据发布、发布配置的修改,编辑和测试、发布模块的修改和
- 全国铁路线路数据.rar
- Vue开源项目Pure Admin二次开发:实现前后端柱状图
- 2000-2023年全国各市CPI数据集.xlsx
- 2000-2023年全国+各省通货膨胀率数据集.xlsx
- 纯电动汽车电池系统HIL测试库
- Java+JSP+Mysql实现Web学生图书管理系统源码+数据库
- 基于SSM框架的农业信息管理系统的实现
- 自己毕业论文配套代码,B站有讲解 和运行效果
- Java+JSP+Mysql实现Web学生图书管理系统源码
- 可靠有效springboot使用netty搭建TCP服务器
- Firefox-latest.exe
- Modbus测试与仿真.rar
- PCIE参考时钟架构详解:同源与非同源的区别
- Java+JSP+Mysql实现Web学生图书管理系统
- 新年海报,讲稿,文案封面
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功