一些经典算法

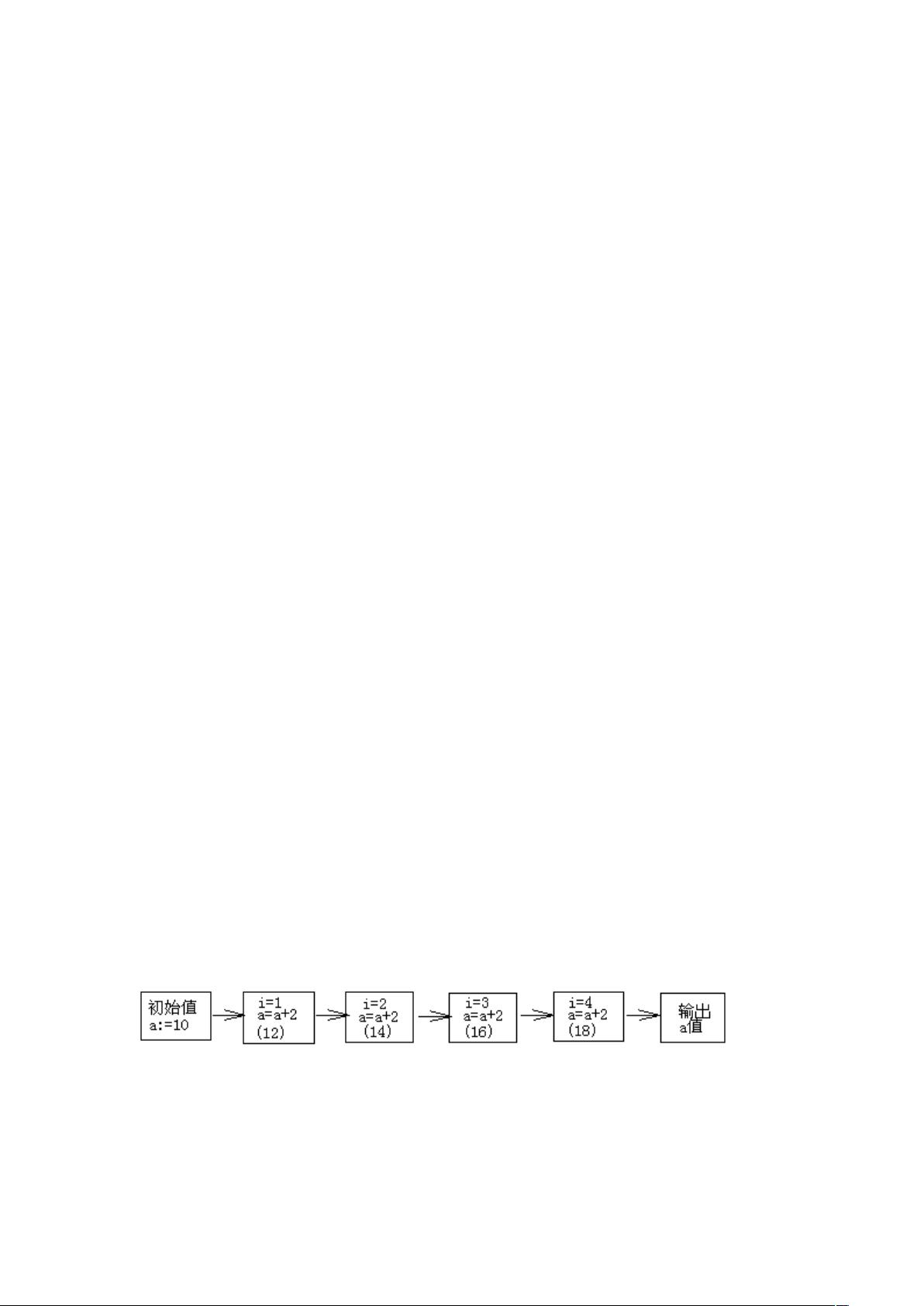
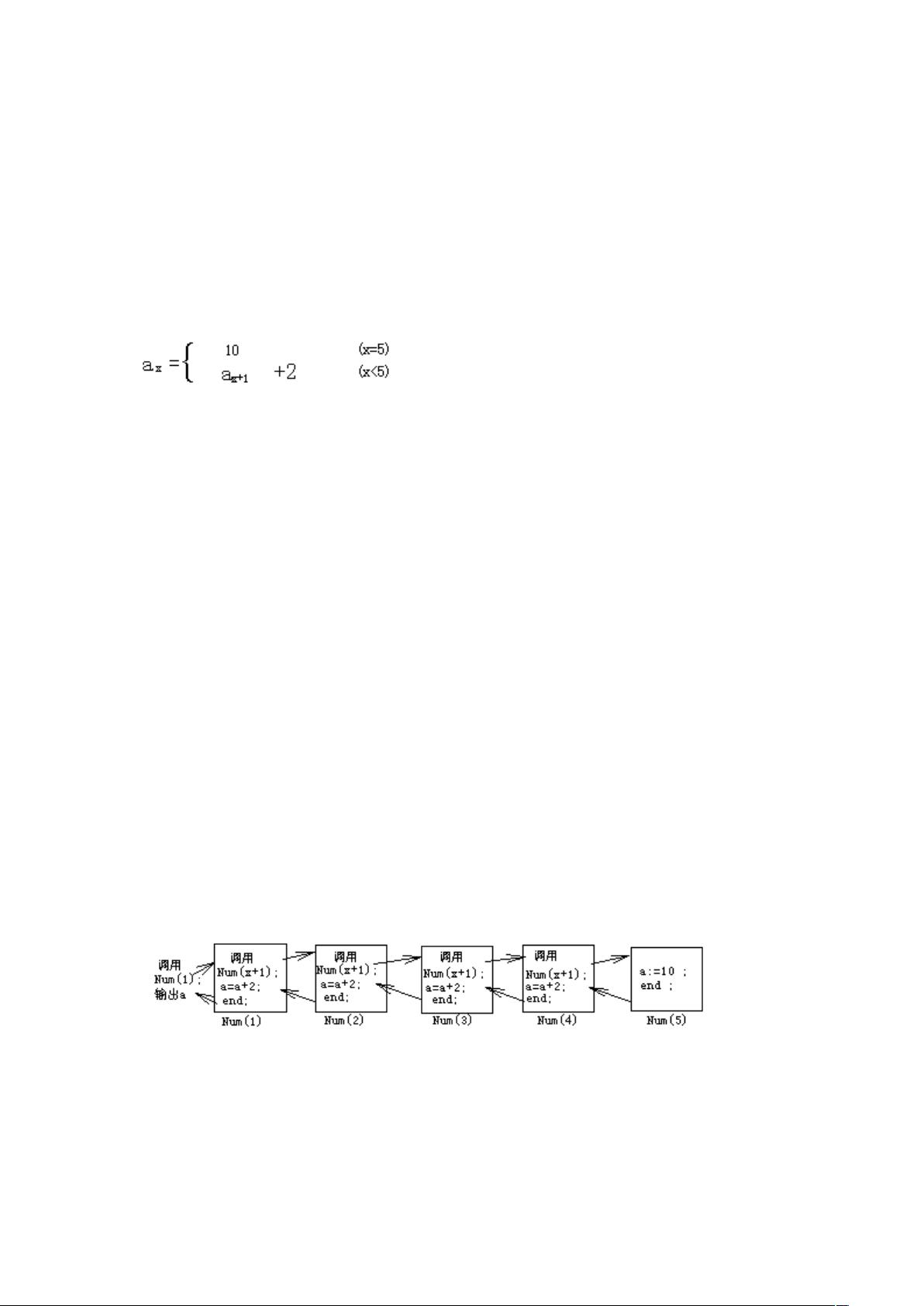
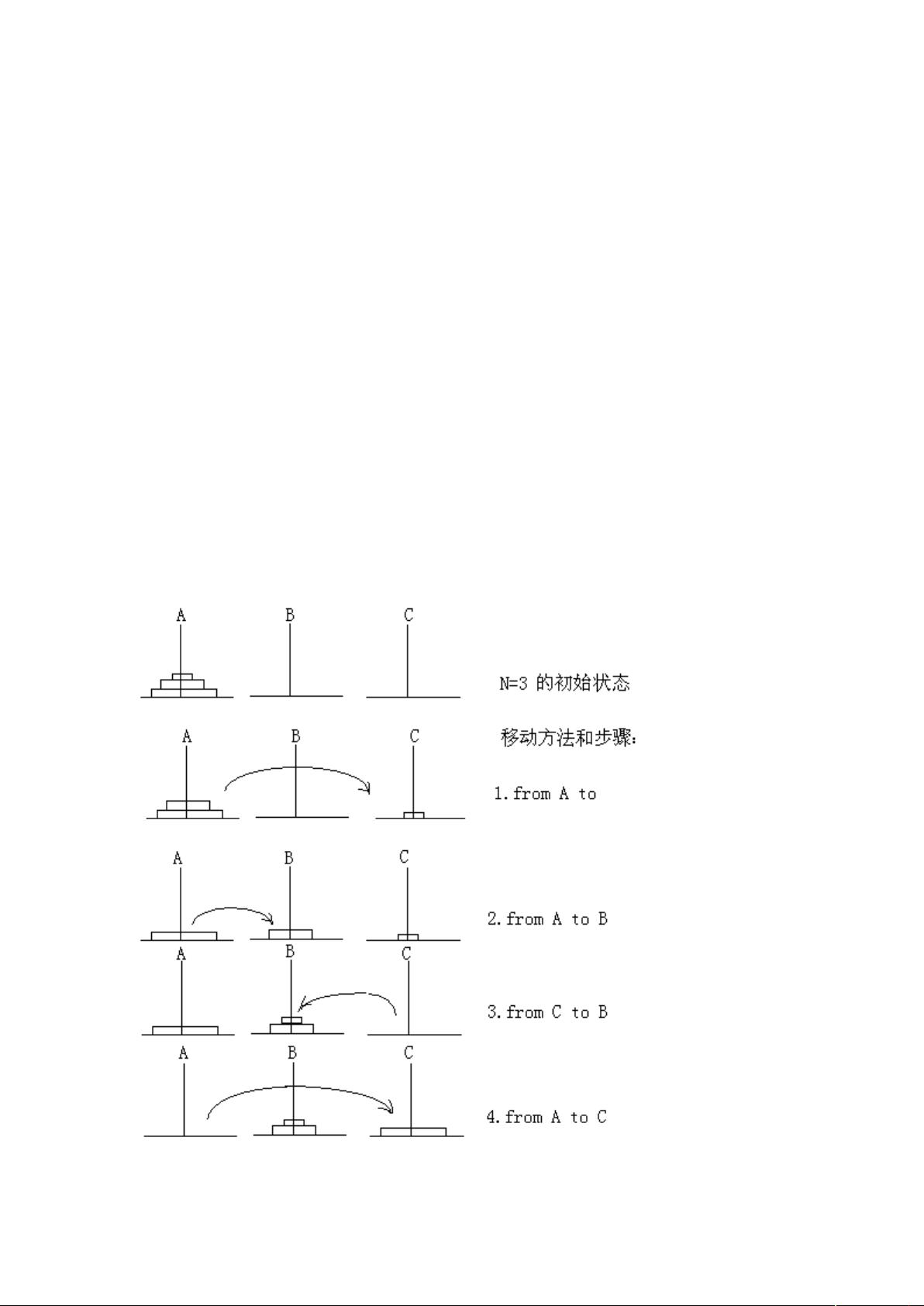
：“一些经典算法” ：“这是摘录的一部分算法，以Pascal语言描述。” ：“经典算法” 【部分内容】：涉及到递推与递归算法 在这个话题中，我们关注的是两种基本的编程算法：递推和递归。这两种方法在解决复杂问题时非常有用。 一、递推算法 递推算法是一种通过一系列简单的运算步骤来描述复杂问题的方法。例如，在一个植树活动的问题中，每位同学种植的树比前一位多两棵。通过递推，我们可以从最后一位同学的植树数量（10棵）开始，向前逐步推算每一位同学种植的树的数量。Pascal程序演示了如何使用循环实现这一递推过程： ```pascal Program Exam1; Var i, a: byte; begin a := 10; for i := 1 to 4 do a := a + 2; writeln('The Num is', a); readln end. ``` 递推的关键在于从一个初始值（起点）开始，遵循相同的运算规则，反复运算直到达到终止条件。它通常可以通过循环结构实现，呈现出单向推进的特性。 二、递归算法 递归算法是一种解决问题的方法，该方法定义为与原始问题的解决方案相同的过程，并在解决问题的过程中调用自身定义的函数或过程。以同一植树问题为例，我们可以将求解第一位同学植树数量的问题转化为一系列求解后续同学数量的子问题，最终通过递归调用来解决。Pascal程序如下： ```pascal Program Exam1_1; Var a: byte; Procedure Num(x: integer); begin if x=5 then a:=10 else begin Num(x+1); a:=a+2; end end; begin Num(1); writeln('The Num is ', a); readln end. ``` 递归的特点包括： 1. 调用过程时需要提供具体参数。 2. 子问题的调用中，参数会不断变化。 3. 每次递归调用都会创建一个新的程序执行层。 4. 边界条件满足时，不再调用，而是执行后续语句并返回上一层。 5. 整个递归过程就像双向运动，先递进到然后逐层返回并带回新的计算结果。 除了植树问题，递归还可以用于其他各种问题，如计算阶乘（X^n）。递归算法的解法可以表示为： ```pascal Procedure Factorial(n: integer; var fact: integer); begin if n = 0 then fact := 1 else begin Factorial(n - 1, fact); fact := fact * n; end; end; var num, fact: integer; begin num := 5; Factorial(num, fact); writeln('Factorial of ', num, ' is ', fact); readln; end. ``` 在这个例子中，计算X^n（5的阶乘）被分解为X^(n-1)，直到n=0时停止递归，并返回1作为基础情况。 总结： 递推和递归都是强大的算法工具，它们在程序设计中有着广泛的应用。递推适用于可以从已知状态推导出未知状态的情况，而递归则适用于问题可以分解为更小的相似子问题的场景。理解并熟练掌握这两种算法对于提升编程技能至关重要。