东北大学数值分析课件

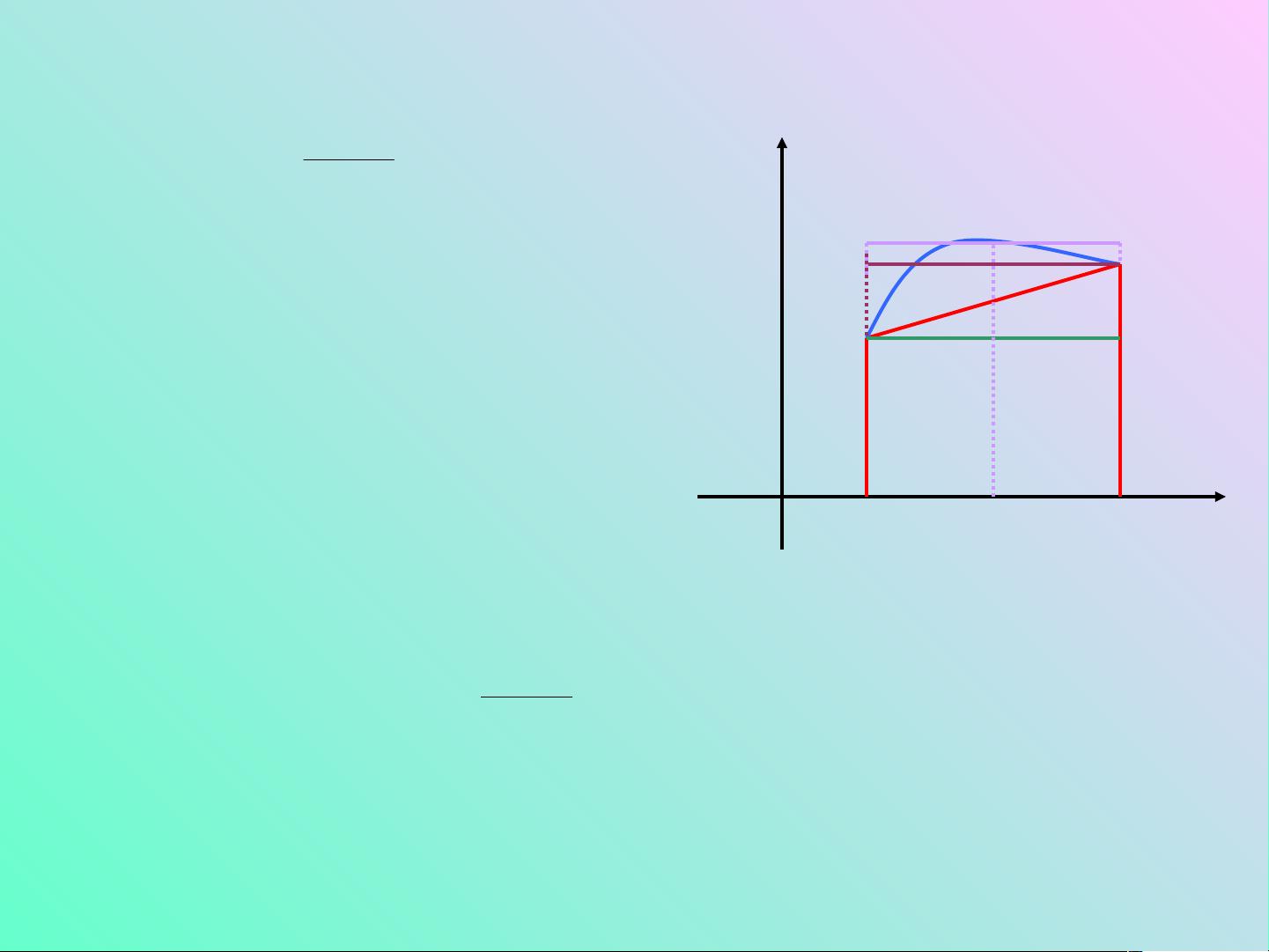
数值分析是数学的一个分支，它涉及使用数值方法来解决数学问题，特别是在计算机上处理复杂数学模型时。东北大学的这门数值分析课件很可能包含了一系列关于这个主题的讲义、幻灯片、练习题和可能的解答，旨在帮助学生理解和应用数值计算技术。 在数值分析中，我们关注的主要知识点包括但不限于以下几个方面： 1. **误差分析**：在实际计算过程中，由于浮点运算的有限精度、舍入误差以及近似方法的使用，误差是不可避免的。数值分析探讨如何量化这些误差并控制它们对结果的影响。 2. **线性代数问题的解法**：如高斯消元法、LU分解、QR分解、奇异值分解（SVD）等，这些都是解决线性方程组和矩阵问题的基本工具。 3. **非线性方程求解**：包括牛顿迭代法、二分法、割线法等，用于找到函数零点。 4. **插值与拟合**：如拉格朗日插值、牛顿插值、样条插值，以及最小二乘法在数据拟合中的应用。 5. **数值微积分**：包括梯形法则、辛普森法则、高斯积分等，用于近似求解定积分。 6. **常微分方程（ODE）求解**：Euler方法、龙格-库塔方法（如四阶Runge-Kutta）等，用于模拟动态系统。 7. **偏微分方程（PDE）的数值方法**：如有限差分法、有限元法、边界元法，用于求解物理、工程等领域中的复杂问题。 8. **最优化问题**：梯度下降法、牛顿法、拟牛顿法，以及在约束优化中的拉格朗日乘子法。 9. **随机数值方法**：蒙特卡洛方法在统计模拟和概率计算中的应用。 通过东北大学的数值分析课程，学生将深入理解这些概念，并学习如何在实践中运用它们。课件可能涵盖了理论讲解、实例分析、编程实践等内容，旨在提升学生的理论素养和解决实际问题的能力。对于工程、物理、经济、金融等领域的专业人员，掌握数值分析的方法和技术是至关重要的，因为这些领域经常需要处理复杂的数值计算问题。