隐马尔可夫模型简介
刘群
2001-6-11
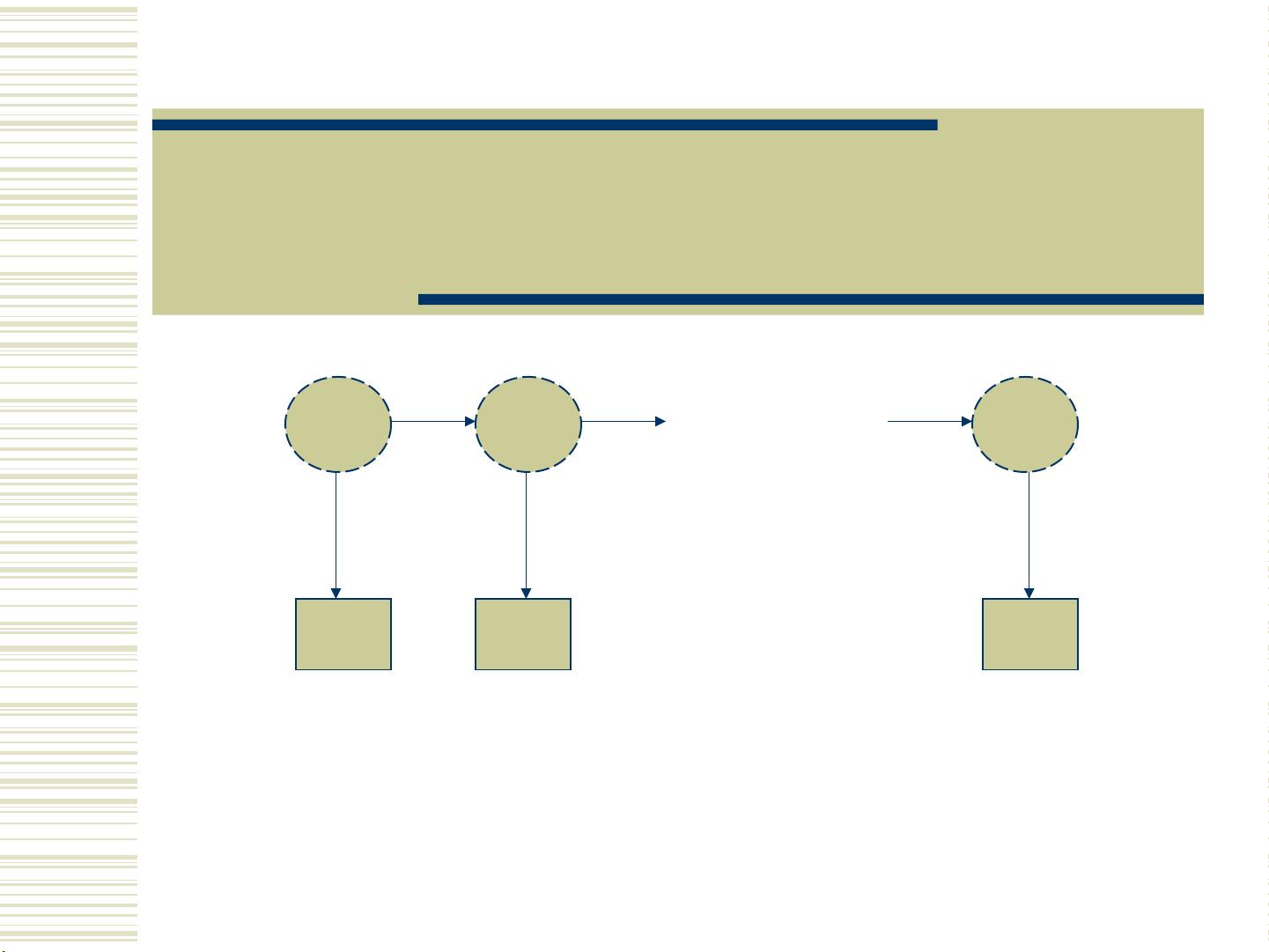
X
1
X
2
X
T
…………
O
1
O
2
O
T
…………
假设
对于一个随机事件,有一个观察值序列: O
1
,...,O
T
该事件隐含着一个状态序列: X
1
,...,X
T
假设 1 :马尔可夫假设(状态构成一阶马尔可夫链)
p(X
i
|X
i-1
…X
1
) = p(X
i
|X
i-1
)
假设 2 :不动性假设(状态与具体时间无关)
p(X
i+1
|X
i
) = p(X
j+1
|X
j
) ,对任意 i,j 成立
假设 3 :输出独立性假设(输出仅与当前状态有关)
p(O
1
,...,O
T
| X
1
,...,X
T
) = Π p(O
t
| X
t
)
定义
一个隐马尔可夫模型 (HMM) 是一个五元组:
(Ω
X
, Ω
O
, A, B, π )
其中:
Ω
X
= {q
1
,...q
N
} :状态的有限集合
Ω
O
= {v
1
,...,v
M
} :观察值的有限集合
A = {a
ij
} , a
ij
= p(X
t+1
= q
j
|X
t
= q
i
) :转移概率
B = {b
ik
} , b
ik
= p(O
t
= v
k
| X
t
= q
i
) :输出概率
π = {π
i
} , π
i
= p(X
1
= q
i
) :初始状态分布
问题
令 λ = {A,B,π} 为给定 HMM 的参数,
令 σ = O
1
,...,O
T
为观察值序列,
隐马尔可夫模型( HMM )的三个基本问题:
1. 评估问题:对于给定模型,求某个观察值序列的
概率 p(σ|λ) ;
2. 解码问题:对于给定模型和观察值序列,求可能
性最大的状态序列;
3. 学习问题:对于给定的一个观察值序列,调整参
数 λ ,使得观察值出现的概率 p(σ|λ) 最大。

















- 1
- 2
- 3
前往页