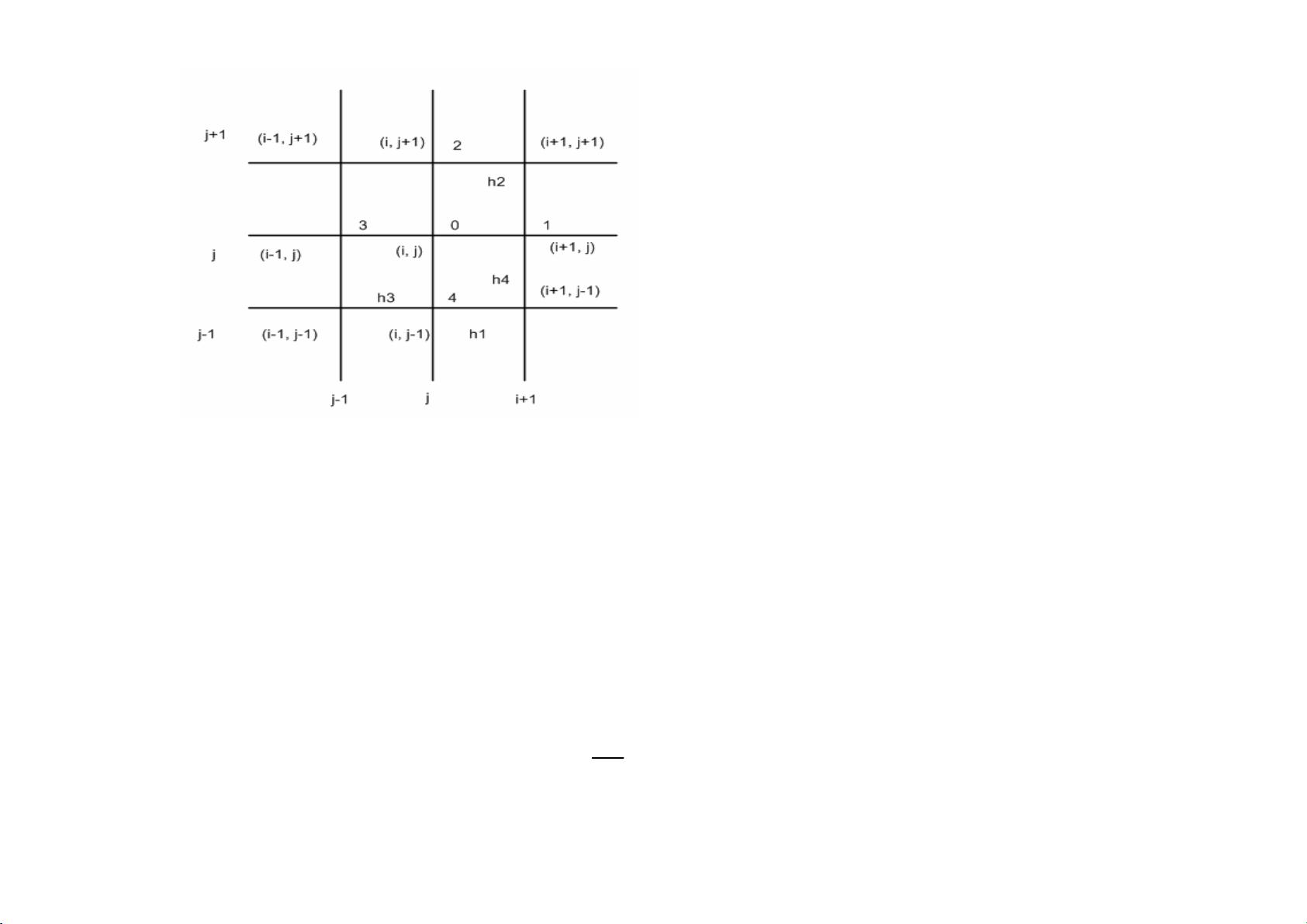
### 有限差分方法简介
#### 一、概述与基础知识
有限差分方法是一种广泛应用于数值分析中的技术，尤其在解决偏微分方程问题时非常有用。它通过将连续的微分方程转化为一系列离散的代数方程组来求解。这种方法的核心思想在于用差商来近似导数，从而将微分方程转化为可以在计算机上求解的形式。
#### 二、一阶微分的差分近似
在一阶微分的差分近似中，最常见的有三种方法：中心差分、向前差分和向后差分。
**中心差分**：
\[
f'(x_i) \approx \frac{f(x_i + h) - f(x_i - h)}{2h} \quad (4.1.3)
\]
这是一种二阶精度的近似，因为它消除了与\(h^1\)相关的误差项。
**向前差分**：
\[
f'(x_i) \approx \frac{f(x_i + h) - f(x_i)}{h} \quad (4.1.4)
\]
这是一种一阶精度的近似。
**向后差分**：
\[
f'(x_i) \approx \frac{f(x_i) - f(x_i - h)}{h} \quad (4.1.5)
\]
这也是一个一阶精度的近似。
#### 三、二阶微分的中心差分近似
对于二阶导数的近似，我们使用中心差分公式：
\[
f''(x_i) \approx \frac{f(x_i + h) - 2f(x_i) + f(x_i - h)}{h^2} \quad (4.1.6)
\]
#### 四、拉普拉斯算符的近似
拉普拉斯算符是对一个函数在各坐标方向上的二阶导数之和。在二维空间中，它可以被近似为：
\[
\nabla^2 f(0) \approx \frac{4}{h^2}(f_2 + f_3 + f_4 - 3f_0) \quad (4.1.7)
\]
这里的\(f_0, f_1, f_2, f_3, f_4\)分别是中心点及其四个相邻点上的函数值。
#### 五、有限差分法与偏微分方程
在处理偏微分方程时，有限差分法的应用尤为广泛。例如，在边界值问题中，我们需要找到满足一定边界条件的解。边界条件可以分为三种类型：
1. **第一类边界条件**（Dirichlet边界条件）：
\[
\phi|_{\Gamma} = g \quad (4.2.3)
\]
这里\(g\)是在边界\(\Gamma\)上的已知函数值。
2. **第二类边界条件**（Neumann边界条件）：
\[
\frac{\partial \phi}{\partial n}|_{\Gamma} = g \quad (4.2.4)
\]
这里\(g\)是在边界\(\Gamma\)上的已知法向导数。
3. **第三类边界条件**（混合边界条件）：
\[
a\phi|_{\Gamma} + b\frac{\partial \phi}{\partial n}|_{\Gamma} = g \quad (4.2.5)
\]
#### 六、泊松方程的有限差分形式
泊松方程是一个典型的椭圆型偏微分方程，其形式为：
\[
\Delta \phi = q(x,y) \quad (4.2.6)
\]
这里\(\Delta\)是拉普拉斯算子，\(q(x,y)\)是给定的源项。泊松方程的有限差分形式为：
\[
\phi_{i+1,j} + \phi_{i-1,j} + \phi_{i,j+1} + \phi_{i,j-1} - 4\phi_{i,j} = h^2 q_{i,j} \quad (4.2.21)
\]
当\(q(x,y) = 0\)时，泊松方程简化为拉普拉斯方程：
\[
\phi_{i+1,j} + \phi_{i-1,j} + \phi_{i,j+1} + \phi_{i,j-1} - 4\phi_{i,j} = 0 \quad (4.2.23)
\]
#### 七、边界条件的离散化处理
在二维情况下，边界条件的离散化处理包括以下几种方法：
1. **直接转移法**（零次插值法）：
当网格边界节点恰好位于物理边界上时，直接将边界条件赋予这些节点。
2. **线性插值法**：
如果边界节点不在物理边界上，可以通过线性插值来估计边界条件值。例如，在\(x\)方向上：
\[
\phi_0 \approx \phi_1 + \frac{(x_0 - x_1)}{(x_1 - x_2)} (\phi_2 - \phi_1)
\]
通过以上讨论，我们可以看到有限差分方法不仅能够有效地将复杂的微分方程转化为易于计算机求解的形式，而且还能够在处理边界条件时提供灵活多样的解决方案。这对于解决实际工程和科学计算问题具有重要意义。
