TCP_Programming_Tutorial.pdf资源-CSDN文库

需积分: 1 80 浏览量 2018-10-02 19:24:54 上传评论收藏 141KB PDF 举报

资源推荐

资源详情

资源评论

Fast Point-Feature Label Placement Algorithm for Real Time

Screen Maps

Missae Yamamoto, Gilberto Camara, Luiz Antonio Nogueira Lorena

National Institute of Space Research - INPE, São José dos Campos, SP, Brazil

São José dos Campos – SP – Brazil

{missae, gilberto}@dpi.inpe.br, lorena@lac.inpe.br

Abstract. The generation of good label placement arrangements is a frequent

problem when producing maps. The objective of a good label placement is to

display the geographic position of the features with their matching label in a

clear and harmonious fashion, following accepted cartographic conventions.

In this work, we propose the fast algorithm for label placement (FALP) for

generation of real time screen maps. FALP is a cost-effective choice, with

good quality performance and excellent runtime performance.

1. Introduction

Point label placement refers to insertion of text in maps and is a challenging problem in

geoinformatics and automated cartography (Wolff and Strijk 1996). Text positioning

requires avoiding overlaps and adherence to cartographic conventions and preferences.

There should be unambiguous association between each text and its matching feature.

Overall, good labeling needs harmony and quality in the resulting maps. The motivation

for research in automated label placement includes:

• Label placement is a fundamental part of producing good maps and essential

item to communicate spatial information;

• Placing text manually in maps is a laborious procedure;

• A good label placing algorithm brings a substantial increase in map productivity;

Label placement would be much simpler if labels could be pre-computed for

each layer at once and their position stored beforehand. Unfortunately, this is not

possible. Map production frequently requires information from more than one layer. It is

the last step in map production. After the user chooses the output layers, the scale and

the limits of the map, object labels need to be placed effectively.

Screen maps are created as answers to spatial queries on geographical

information systems (GIS), either in desktop or Web applications. To allow for a

smooth uninterrupted response, the maps must be produced “on the stroke of a key”.

Otherwise, the user gets impatient. Screen map production needs to balance the quality

of label placement with the processing time. Label placement techniques that are of

extremely good quality but need much processing time are not useful for screen maps.

The most common label placement problem is the point feature label placement

(PFLP) problem. Given a set of places associated to point locations, the PFLP consists

in placing the names of these places in the map with quality and efficiency. This work

describes the Fast Algorithm for Label-Placement (FALP) to solve the PFLP. Our

results show the FALP has good performance in label placement processing time and

presents a good label placement quality for a screen map. Given its relative simplicity of

implementation and efficient performance, we believe that FALP method is a good

solution to the PFLP problem for screen maps.

In Section 2 of the paper, we review the literature on label placement. In Section

3, we present the conflict graph, a structure that represents all conflicts between

candidate labels. Section 4 we introduce the FALP algorithm. Section 5 shows

computational results using instances formed by standard sets of randomly generated

points suggested in the literature.

2. Review of the point label placement problem

There are three different label-placement problems: labeling of point features (cities,

schools, hospital, mountain peaks …), line features (rivers, roads, …), and area features

(countries, states, oceans, …). In this article we focus on placing labels for point

features using combinatorial optimization. We will use three key notions, defined

below:

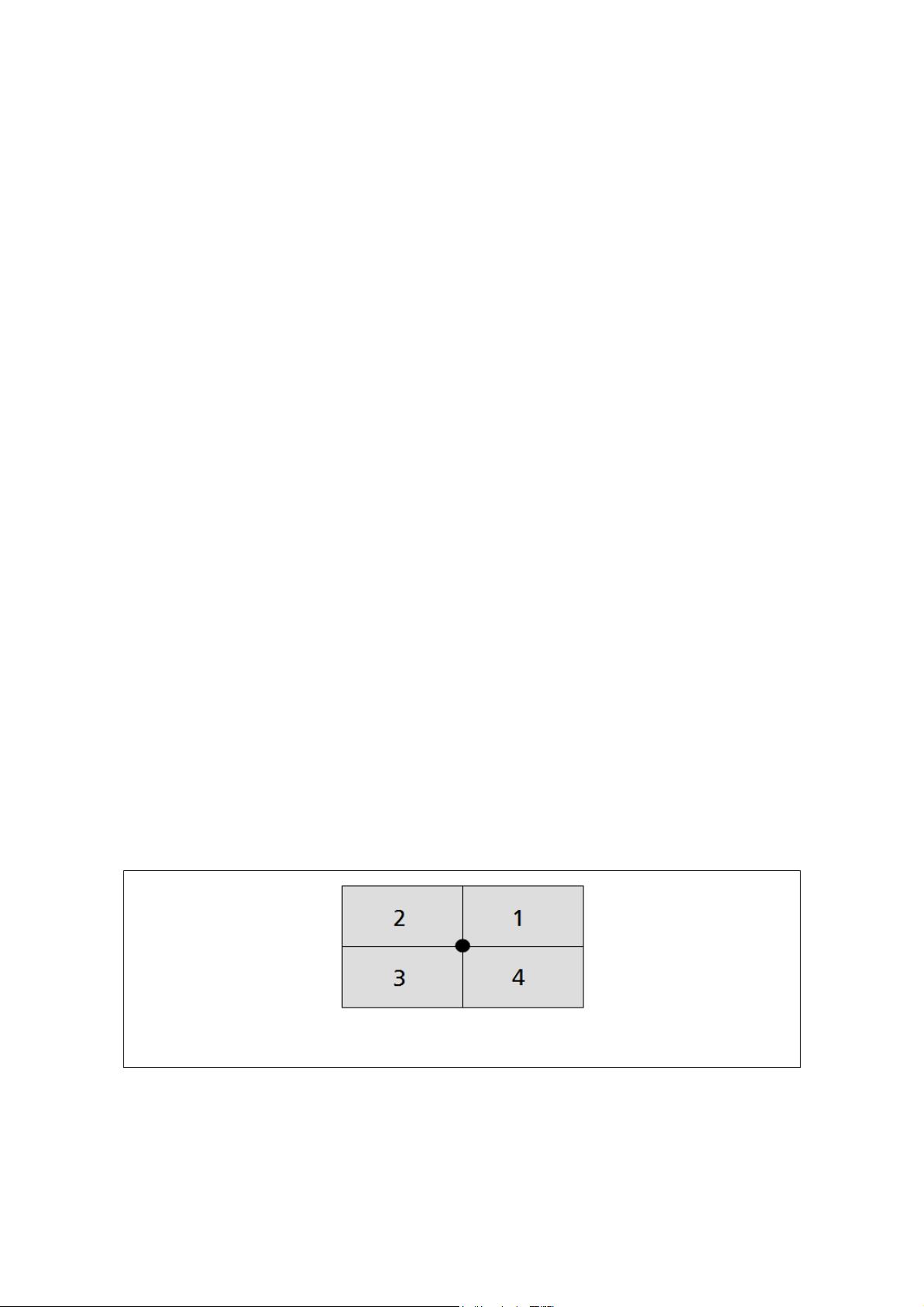
• Label positions for each point feature. Given a point, a label can be placed on

one of four positions relative to it (see Figure 1). Therefore, a label position is an

ordered pair (point location, relative position). In Figure 1, each box marks a

label position.

• Cartographic preference. Usually, we prefer to place labels at the upper right

corner of the point, and this preference decreases counterclockwise from this

position. The value inside each box in Figure 1 matches the order of

cartographical preference for placing a label. Lower values mark more desirable

positions.

• Objective function. The objective function (f) measures the quality of the label

placement. The quality of labeling depends on the number of overlaps between

labels and the cartographic preference for label placement.

Figure 1. A set of label positions and their cartographic preference (best = 1;

worse = 4)

We take npos as the number of label positions and take np as the total number of

point features. There are npos

possible arrangements, a number which increases

exponentially. Since the set of possible solutions is finite, theoretically we could select

the best solution by enumeration. As the number of points increases this becomes

unfeasible, because of the combinatorial explosion of possible solutions. Marks and

Scheiber (1991) have shown the point feature label placement (PFLP) problem is NP-

hard.

For screen maps, we need algorithms that seek a compromise solution in cost-

benefit, with good quality and a short response time. In our algorithm, we have

considered a limited set of four possible label positions. Our approach can be extended

to account for a larger number of positions. However, a larger set of the label positions

would result in a problem with larger number of possible solutions. In spite of the

apparent better looking results, the growth in problem complexity results in a much

higher computational effort. We consider that a set of four positions to be an acceptable

compromise in terms of cost-benefit analysis.

Several heuristics and metaheuristics have been used for the PFLP problem. For

an early review of methods, see Christensen et al. (1995), which includes Zoraster's

integer programming algorithm (Lagrangean relaxation) (Zoraster 1990) and Hirsch's

continuous gradient-descent algorithm (Hirsch 1982). Relevant recent proposals include

solutions based on simulated annealing (Christensen et al. 1995), genetic algorithms

(GA) (Verner et al. 1997) and tabu search (Yamamoto et al. 2002). The most recent

result is the constructive genetic approach (Yamamoto and Lorena 2005), that has better

results in label placement quality than all previous methods.

In this paper, we will consider the PFLP as the problem of placing labels in all

points. We will try to find out the largest subset of labels with no conflicts with good

quality at acceptable runtime. Our algorithm considers that a typical generation of screen

maps consists of three steps:

• The user requests an overview of the area of interest. The software

displays the area, with a suitable choice of labels depicted at that scale.

• The user requests a zoom in an area for detailed analysis. The software

displays the area, and labels invisible at the largest scale are made visible

at this scale.

• The user may zoom for further detail or pan for visualization of

neighboring areas. In the latter case, more labels will be made visible and

the software will try to display them.

Based on this conception, we consider that label placement on screen maps

needs a preparation stage, where the software will build a list of labels which will be

visible at different scales. This pre-processing phase is outside the scope of this paper.

The proposed algorithm will run at one particular scale, where the visible labels are

known in advance. Therefore, our algorithm should be embedded in a more general

visualization software. In the proposed method, the basic data structure is the conflict

graph, described in the next section.

3. The conflict graph

The conflict graph is a structure that describes conflicts due to label overlap. Each node

of the conflict graph is a label position. Recall from section 2 that we consider a label

position as a pair (point location, relative position). The edges of the graph link

conflicting label positions. Figure 2 shows two points with their label positions and the

剩余14页未读，继续阅读

评论收藏

内容反馈

suhebater

粉丝: 0
资源: 1

TCP_Programming_Tutorial.pdf

operating_system_tutorial.pdf

CMSIS_RTOS_Tutorial.zip

LoadRunner12_Chinese_tutorial.pdf.zip

2019_icip_tutorial.pdf

1_SimscapeMultibody_Tutorial.zip

4_cifar10_tutorial.ipynb

Lean_Software_Development_Tutorial.pdf

3_neural_networks_tutorial.ipynb

python_numpy_tutorial.ipynb

CMSIS_RTOS_Tutorial.pdf

System_Verilog_Tutorial_0315.doc.pdf

A_Genetic_Algorithm_Tutorial.Darrell_Whitley.[EN]

TCP_UDP_Tutorial.pdf

Linux_命令行_Bash_的基本用法和脚本编程_-_阮一峰__bash-tutorial.zip

dvcon_eu_2016_fv_tutorial.pdf

MSTAR(PD2_EMMI_Training_Pack_v2.0)

INCA_Tutorial_R7.2_R02_EN.pdf

OpenCV_object_detection_tutorial.ipynb

The_Java_EE5_Tutorial.rar_Java ee5 CHM_java ee5 tutorial_java e

Fluent_Workbench_Tutorial_Package_2021_R2.zip

1_tensor_tutorial.ipynb

Deep_Learning_Tutorial_0.1.pdf.pdf

soatest5.5_Tutorial.pdf&soatest_Tutorial.pdf

EDEM_add-in_for_ANSYS_Workbench_-_Dump_truck_tutorial .zip

TensorFlow_2.x_tutorial.ipynb

ANSYS_Fluent_Tutorial_Guide_2021_R1.pdf

neural_style_tutorial.py

char_rnn_generation_tutorial_CN.ipynb

5_data_parallel_tutorial.ipynb

最新资源