他姓許i
- 粉丝: 7
- 资源: 17
最新资源
- PS5游戏服务网站的设计与实现-springboot毕业项目,适合计算机毕-设、实训项目、大作业学习.zip
- 课程设计基于hadoop实现的图书推荐系统源码+项目说明(高分课设)
- springboot 电商书城平台系统(已调试)-springboot毕业项目,适合计算机毕-设、实训项目、大作业学习.zip
- 432JSP基于SSH2银行业务管理系统毕业课程源码设计+论文资料+任务书+开题报告+答辩ppt
- springboot校园一卡通_q7e7o--论文-springboot毕业项目,适合计算机毕-设、实训项目、大作业学习.zip
- springboot校园便利平台_1jxhb--论文-springboot毕业项目,适合计算机毕-设、实训项目、大作业学习.zip
- 基于vue+python实现在线教育网站的设计与开发
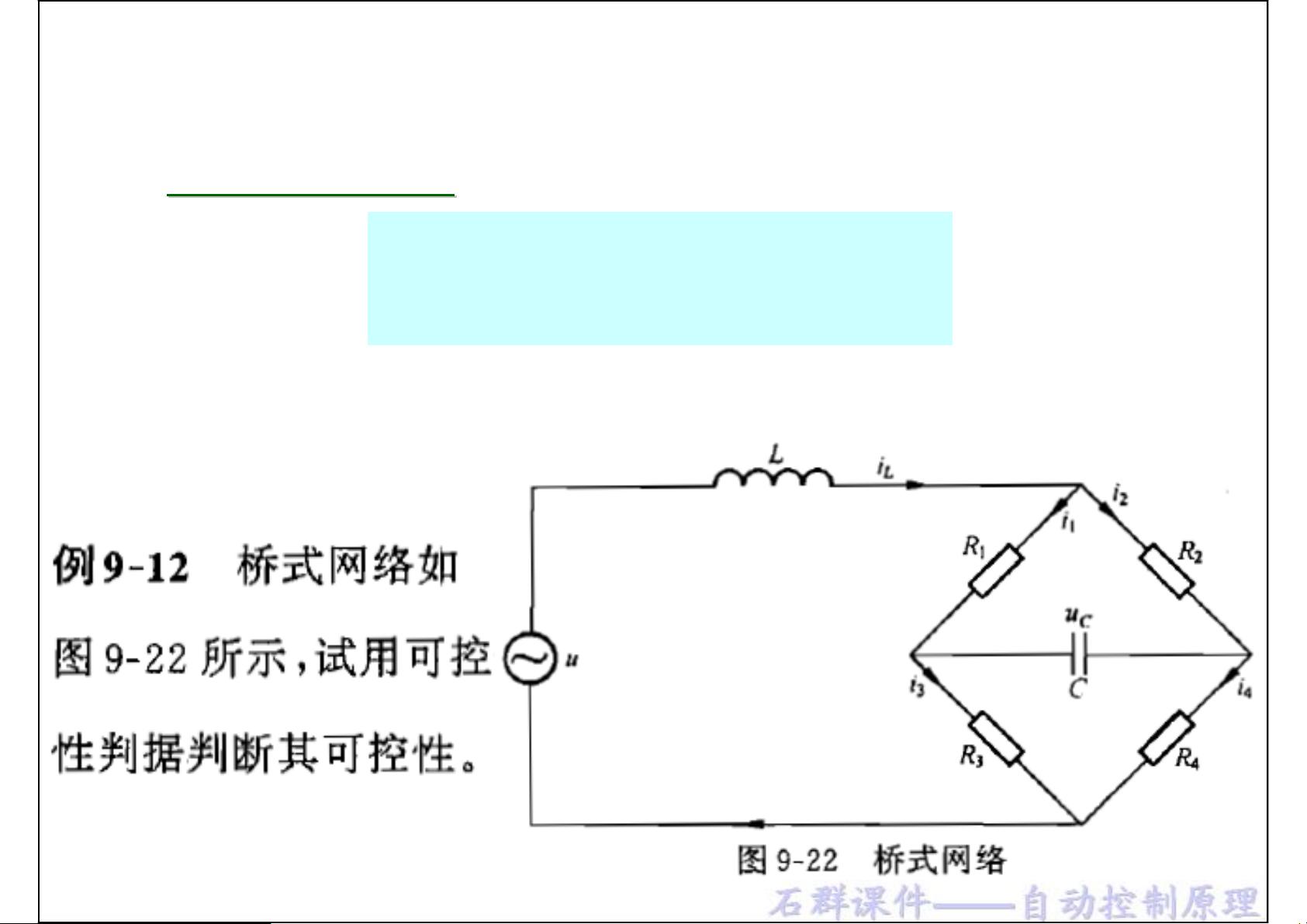
- Matlab小电流接地系统的建模与单相故障的仿真分析(仿真工程文件+结果图+详细设计说明书+介绍PPT) 随着城乡的发展,电力系统开始不断完善,配电网络也的结构也开始复杂,在线缆的铺设上也得到大幅提升
- c语言中自增自减的用法.md
- springboot基于JAVA的企业内部人员绩效量化管理系统_av7p4--论文-springboot毕业项目,适合计算机毕-设、实训项目、大作业学习.zip
- 基于Java的企业OA管理系统的设计与实现-springboot毕业项目,适合计算机毕-设、实训项目、大作业学习.rar
- springboot基于Hadoop短视频流量数据分析与可视化_nduy8--论文-springboot毕业项目,适合计算机毕-设、实训项目、大作业学习.zip
- 基于java的校园服务平台设计与开发-springboot毕业项目,适合计算机毕-设、实训项目、大作业学习.rar
- 基于java无人超市管理系统-springboot毕业项目,适合计算机毕-设、实训项目、大作业学习.zip
- 基于Java的小区物业智能卡管理的设计与实现-springboot毕业项目,适合计算机毕-设、实训项目、大作业学习.zip
- 基于JS的个人云盘管理系统的设计与实现-springboot毕业项目,适合计算机毕-设、实训项目、大作业学习.zip
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈