算法大全matlab全国大学生数学建模材料

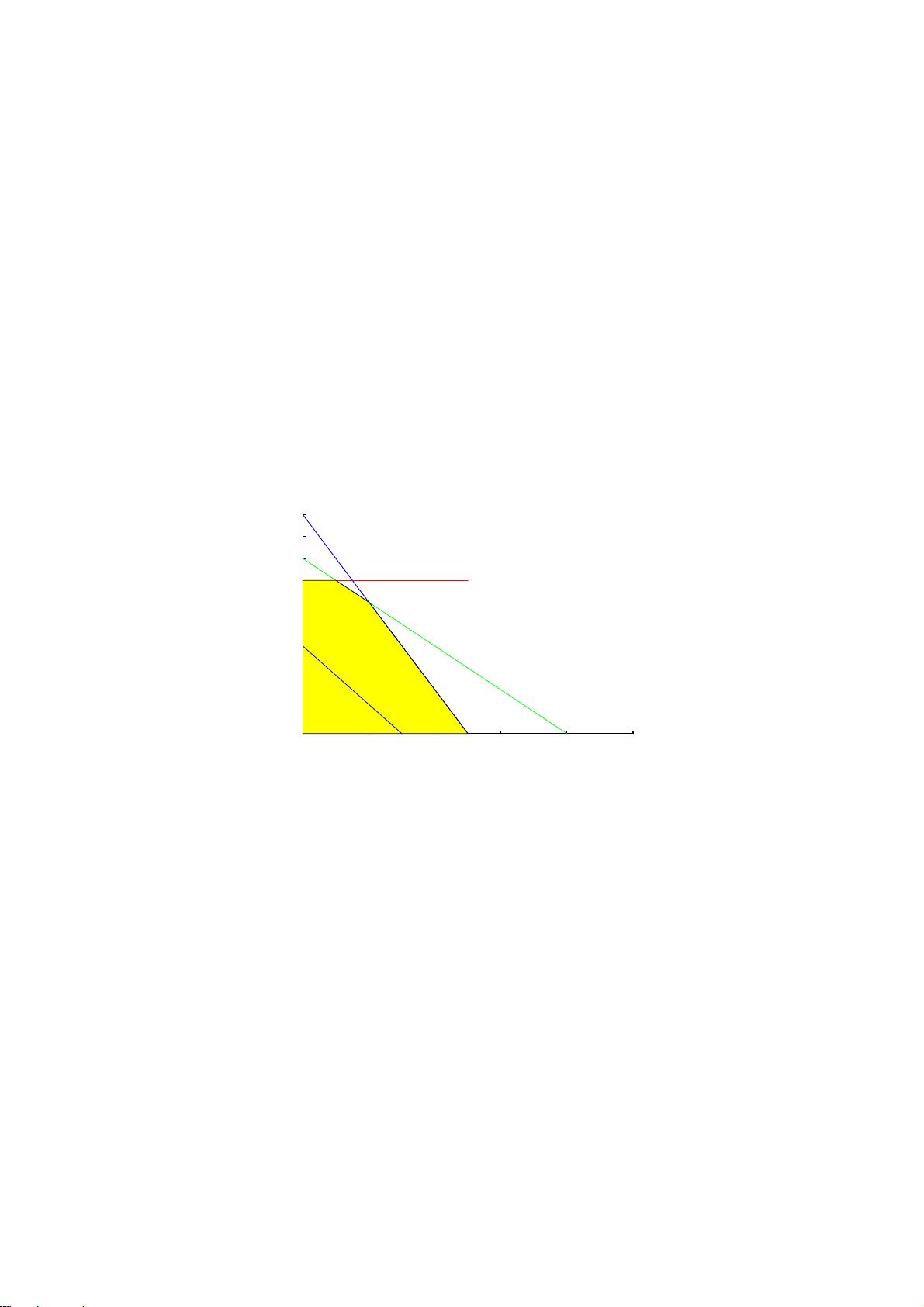
这是一个matlab数学建模用的教材，分30章，每章节都有模型例子和matlab代码例子。数学建模的绝佳材料。matlab数学建模算法大全 matlab建模必备教程.目录如下： 第一章 线性规划 第二章 整数规划 第三章 非线性规划 第四章 动态规划 第五章 图与网络模型及方法 第六章 排队论模型 第七章 对策论 第八章 层次分析法 第九章 插值与拟合 第十章 数据的统计描述和分析 第十一章 方差分析 第十二章 回归分析 第十三章 微分方程建模 第十四章 稳定状态模型 第十五章 常微分方程的解法 第十六章 差分方程模型 第十七章 马氏链模型 第十八章 动态优化模型 第十九章 神经网络模型 第二十章 偏微分方程的数值解 第二十一章目标规划 第二十二章模糊数学模型 第二十三章现代优化算法 第二十四章时间序列模型 第二十五章存贮论 第二十六章经济与金融中的优化问题 第二十七章生产与服务运作管理中的优化问题 第二十八章灰色系统理论及其应用 第二十九章多元分析 第三十章 偏最小二乘回归 根据给定的教材《算法大全MATLAB全国大学生数学建模材料》的内容，我们可以总结出以下相关的知识点： ### 1. 线性规划 #### 1.1 线性规划的基本概念 - **定义**: 线性规划是运筹学的一个分支，主要研究在一系列线性等式或不等式的约束条件下，如何使得一个线性的目标函数达到最大或最小值。 - **应用场景**: 在工业生产、资源分配、成本控制等多个领域有着广泛的应用。 #### 1.2 线性规划的实例分析 - **实例**: 某机床厂生产甲、乙两种机床，每种机床的利润不同，且生产过程受到不同机器加工时间的限制。如何合理安排生产计划以最大化总利润。 - **数学模型**: - **目标函数**: \(z = 4000x_1 + 3000x_2\), 其中\(x_1\)表示甲机床的数量，\(x_2\)表示乙机床的数量。 - **约束条件**: \(\begin{cases} 2x_1 + x_2 \leq 10 \\ x_1 + x_2 \leq 8 \\ x_2 \leq 7 \\ x_1, x_2 \geq 0 \end{cases}\) #### 1.3 MATLAB中的线性规划标准形式 - **标准形式**: \( \min c^Tx \) s.t. \( \begin{cases} Ax \leq b \\ A_{eq}x = b_{eq} \\ lb \leq x \leq ub \end{cases} \) - **实例转换**: 将实例中的最大值问题转换为最小值问题，并调整相应的不等号。 #### 1.4 解的概念 - **可行解**: 满足所有约束条件的解。 - **最优解**: 使得目标函数达到最大（或最小）值的可行解。 - **可行域**: 所有可行解构成的集合。 #### 1.5 图解法 - **基本思想**: 通过绘制目标函数的等值线以及约束条件的图形，找到目标函数最大（或最小）值的解。 - **步骤**: 1. 绘制约束条件的图形。 2. 绘制目标函数的不同等值线。 3. 寻找使得目标函数最大（或最小）的等值线与可行域边界相交的点。 ### 2. 整数规划 - **定义**: 整数规划是指决策变量必须取整数值的优化问题。它可以是纯整数规划（所有决策变量都必须是整数），也可以是混合整数规划（部分决策变量必须是整数）。 - **应用场景**: 生产调度、投资组合选择等领域。 - **解决方法**: 分支定界法、割平面法等。 ### 3. 非线性规划 - **定义**: 当目标函数或约束条件是非线性的时候，就形成了非线性规划问题。 - **应用场景**: 工程设计、经济预测等。 - **解决方法**: 梯度下降法、牛顿法、拟牛顿法等。 ### 4. 动态规划 - **定义**: 动态规划是一种用于解决多阶段决策过程中的最优化问题的方法。 - **应用场景**: 资源分配、路径规划等。 - **关键概念**: 状态、决策、阶段、策略。 ### 5. 图与网络模型及方法 - **定义**: 利用图论和网络理论来解决问题的方法。 - **应用场景**: 最短路径问题、最大流问题等。 - **关键算法**: Dijkstra算法、Ford-Fulkerson算法等。 ### 6. 排队论模型 - **定义**: 研究顾客到达和接受服务的随机过程的理论。 - **应用场景**: 服务业中的顾客等待时间预测、服务质量评估等。 - **关键参数**: 到达率、服务率、排队规则。 ### 7. 对策论 - **定义**: 研究两个或多个参与者之间的策略互动。 - **应用场景**: 游戏策略、市场竞争等。 - **关键概念**: 策略、支付矩阵、纳什均衡。 ### 8. 层次分析法 - **定义**: 一种将定性分析与定量分析相结合的多准则决策分析方法。 - **应用场景**: 决策分析、优先级排序等。 - **关键步骤**: 构建层次结构模型、判断矩阵的构建与一致性检验。 ### 9. 插值与拟合 - **定义**: 插值是寻找一条经过所有已知数据点的曲线的过程；拟合则是寻找一条与已知数据点尽可能接近的曲线的过程。 - **应用场景**: 数据分析、信号处理等。 - **关键方法**: 多项式插值、样条插值、最小二乘拟合等。 ### 10. 数据的统计描述和分析 - **定义**: 对数据进行描述性统计分析，包括中心趋势度量、离散程度度量等。 - **应用场景**: 数据预处理、数据分析等。 - **关键指标**: 平均值、中位数、众数、标准差、方差等。 ### 11. 方差分析 - **定义**: 一种用于比较多个总体均值之间是否存在显著差异的统计方法。 - **应用场景**: 实验设计、质量控制等。 - **关键假设**: 正态分布、方差齐性。 ### 12. 回归分析 - **定义**: 研究自变量与因变量之间关系的一种统计方法。 - **应用场景**: 预测分析、因果关系探索等。 - **关键类型**: 线性回归、多元回归、逻辑回归等。 ### 13. 微分方程建模 - **定义**: 使用微分方程来描述物理或其他系统的变化过程。 - **应用场景**: 物理模拟、生物系统建模等。 - **关键类型**: 普通微分方程、偏微分方程。 ### 14. 稳定状态模型 - **定义**: 描述系统在一定条件下达到的平衡状态。 - **应用场景**: 控制系统设计、热力学系统分析等。 - **关键概念**: 稳态解、稳定性分析。 ### 15. 常微分方程的解法 - **定义**: 解决常微分方程的方法。 - **应用场景**: 数值模拟、控制系统分析等。 - **关键方法**: 欧拉法、龙格库塔法、亚当斯法等。 ### 16. 差分方程模型 - **定义**: 通过差分方程来描述系统变化的模型。 - **应用场景**: 时间序列预测、生态学模型等。 - **关键方法**: 显式差分法、隐式差分法。 ### 17. 马氏链模型 - **定义**: 描述随机过程随时间演化的模型。 - **应用场景**: 随机过程模拟、金融市场分析等。 - **关键概念**: 状态转移概率、平稳分布。 ### 18. 动态优化模型 - **定义**: 求解动态过程中最优策略的模型。 - **应用场景**: 控制理论、供应链管理等。 - **关键方法**: 动态规划、最优控制理论。 ### 19. 神经网络模型 - **定义**: 模拟人脑神经系统的计算模型。 - **应用场景**: 图像识别、自然语言处理等。 - **关键类型**: 前馈神经网络、循环神经网络、卷积神经网络。 ### 20. 偏微分方程的数值解 - **定义**: 解决偏微分方程的方法。 - **应用场景**: 流体力学、电磁场分析等。 - **关键方法**: 有限差分法、有限元法。 ### 21. 目标规划 - **定义**: 一种多目标优化的方法。 - **应用场景**: 资源配置、生产计划等。 - **关键概念**: 目标函数、偏差变量。 ### 22. 模糊数学模型 - **定义**: 利用模糊集合理论来描述不确定性和模糊性。 - **应用场景**: 控制系统设计、决策支持系统等。 - **关键概念**: 模糊集合、隶属度函数。 ### 23. 现代优化算法 - **定义**: 包括遗传算法、粒子群优化算法等智能优化算法。 - **应用场景**: 复杂优化问题求解。 - **关键特点**: 随机搜索、全局寻优能力。 ### 24. 时间序列模型 - **定义**: 用于分析随时间变化的数据序列的模型。 - **应用场景**: 经济预测、天气预报等。 - **关键类型**: 自回归模型、移动平均模型、ARIMA模型。 ### 25. 存贮论 - **定义**: 研究物品存储管理的理论。 - **应用场景**: 库存管理、物资供应等。 - **关键概念**: 存货水平、订货点、安全库存。 ### 26. 经济与金融中的优化问题 - **定义**: 在经济学和金融学中寻求最优解决方案的问题。 - **应用场景**: 投资组合优化、风险评估等。 - **关键方法**: 金融工程、资产定价理论。 ### 27. 生产与服务运作管理中的优化问题 - **定义**: 在生产和服务运作管理中寻求最优资源配置的问题。 - **应用场景**: 生产计划、服务质量改进等。 - **关键方法**: 生产调度、质量控制。 ### 28. 灰色系统理论及其应用 - **定义**: 一种处理不完全信息的方法。 - **应用场景**: 预测分析、决策支持等。 - **关键概念**: 灰色预测模型、灰色关联分析。 ### 29. 多元分析 - **定义**: 对多变量数据进行分析的方法。 - **应用场景**: 数据挖掘、市场调研等。 - **关键技术**: 主成分分析、因子分析、聚类分析。 ### 30. 偏最小二乘回归 - **定义**: 一种用于解决自变量之间存在多重共线性问题的回归方法。 - **应用场景**: 数据分析、预测建模等。 - **关键特点**: 同时考虑解释变量和响应变量的信息。 以上这些章节涵盖了数学建模中的核心内容和技术，从简单的线性规划到复杂的现代优化算法，每种方法都有其独特的应用场景和解决思路。通过学习这些内容，读者不仅能够掌握数学建模的基本技巧，还能深入了解各种高级算法的应用场景，从而在实际问题中灵活运用这些工具和技术。