C++ 动态规划经典案例解析之最长公共子序列（LCS）
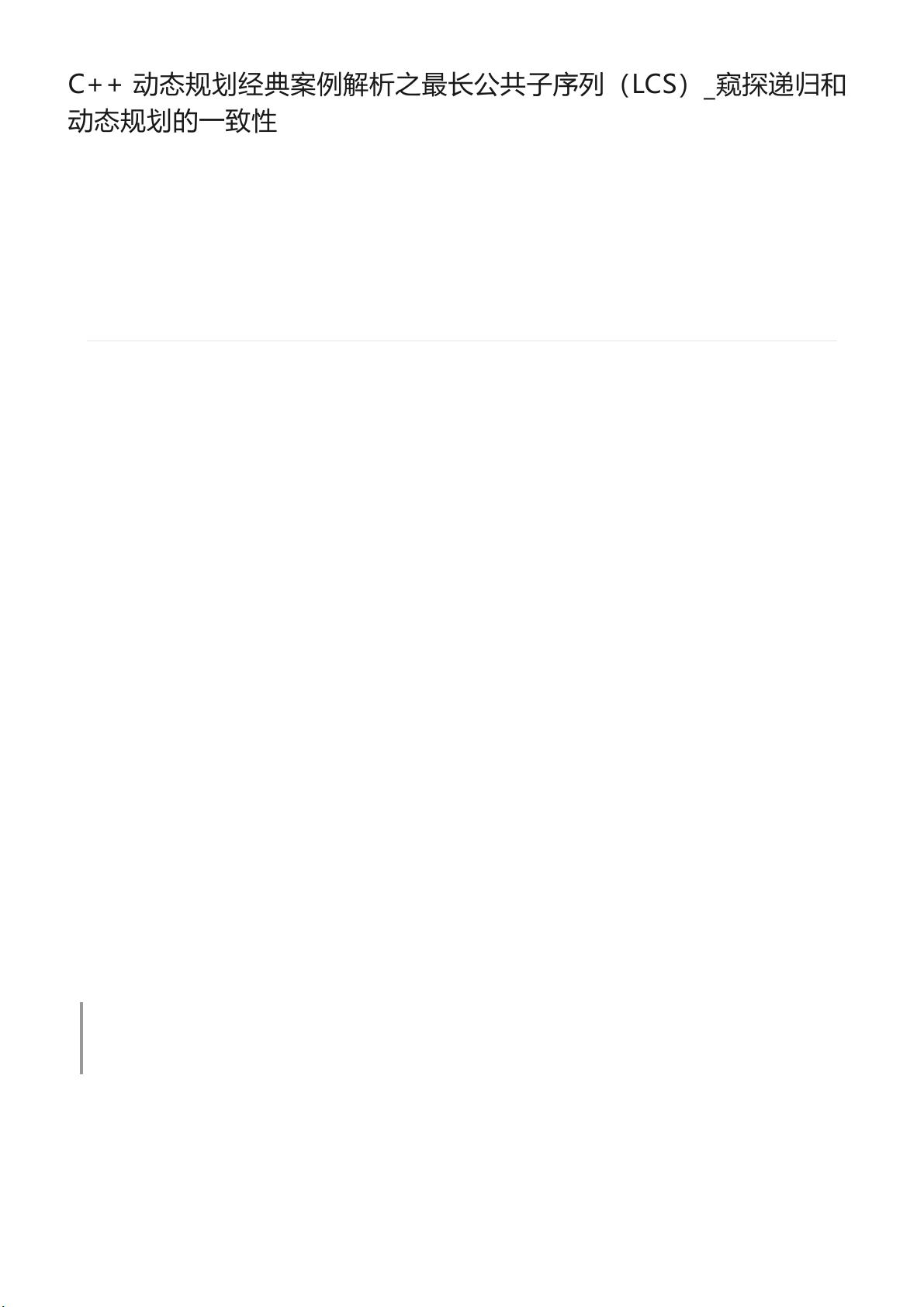
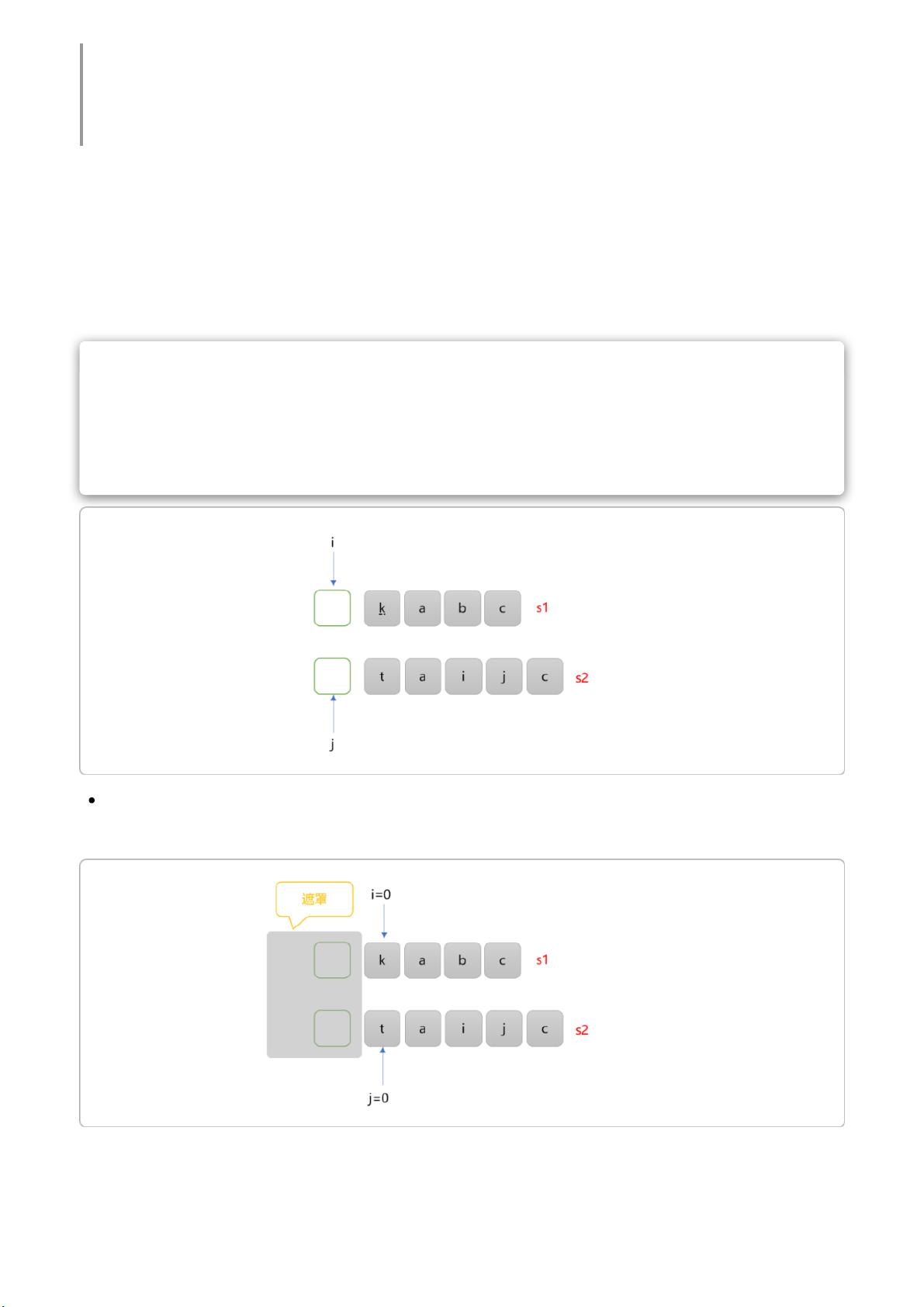
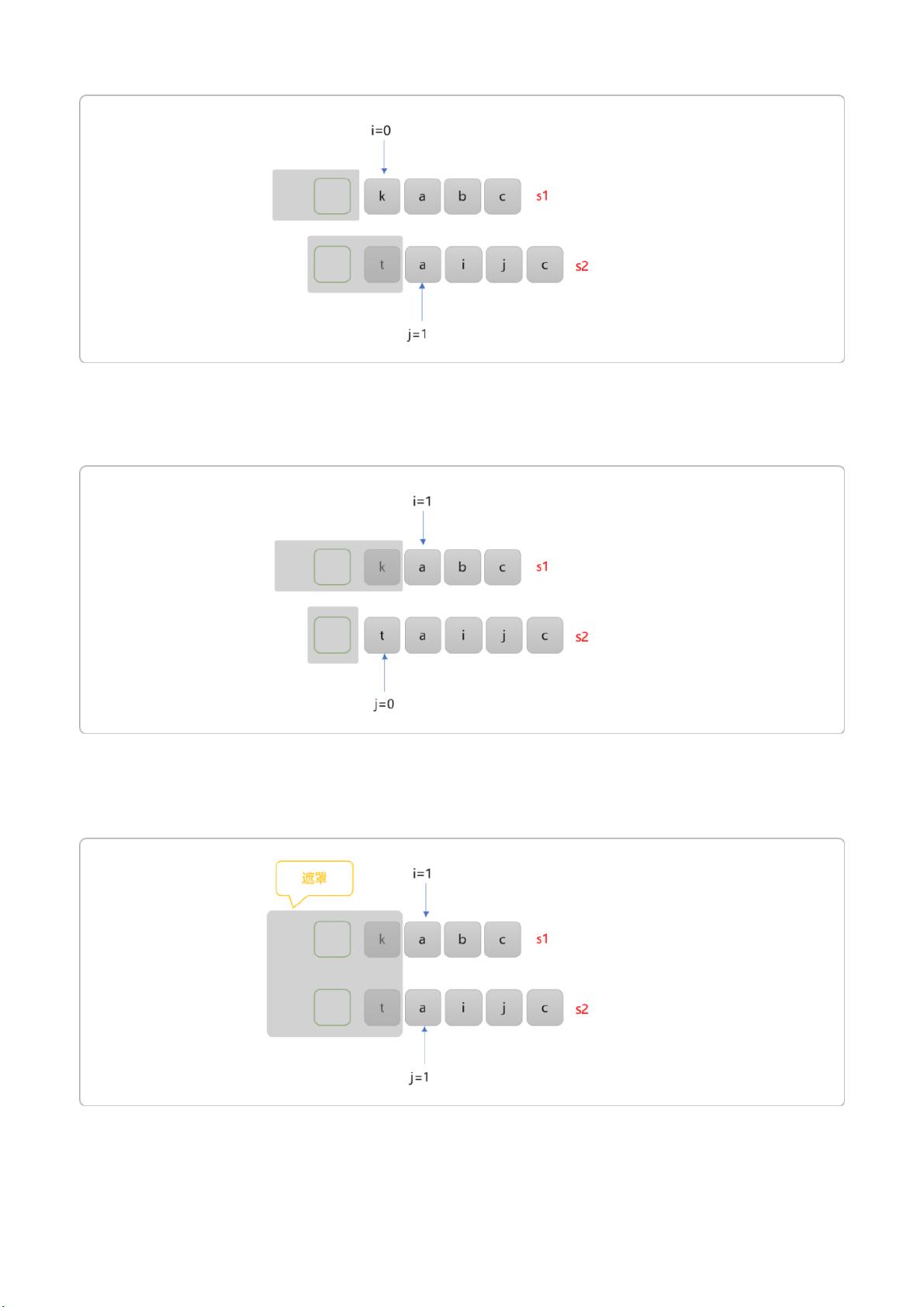
C++ 动态规划是计算机科学中的一种经典算法思想，它可以解决许多实际问题。今天，我们将讨论一个非常经典的案例：最长公共子序列（LCS），它是字符串处理中的一种基本问题。
什么是最长公共子序列？简单来说，就是找出两个或多个字符串中的最长公共子序列。例如，字符串 s1=kabc 和 s2=taijc，其最长公共子序列是 ac。需要注意的是，子序列只要求其中字符保持和原字符串中一样的顺序，而不一定连续。
那么，如何使用递归思想来解决这个问题？我们可以将问题抽象为一个函数，函数的语义是：i 和 j 作为起始位置时字符串 s1,s2 的最长公共子序列。这个函数可以写成：
```c
int lcs(string s1, int i, string s2, int j);
```
如果 s1、s2 为全局变量，函数可以简化为：
```c
int lcs(int i, int j);
```
初始时，i=0 和 j=0 意味着求解完整的 s1 和 s2 的最长公共子序列。此时规模最大，无法直接得到答案。于是，我们把问题延续到规模较小的子问题。
在这里，我们有三种选择：
A、i 不动，j+1。即把 i 指向作为起始位置的 s1 字符串和 j+1 作为起始位置的 s2 字符串继续比较。
B、j 不动，i+1。即把 i+1 指向作为起始位置的 s1 字符串和 j 作为起始位置的 s2 字符串继续比较。
C、i 和 j 同时移动到下一个位置。即把 i+1 指向作为起始位置的 s1 字符串和 j+1 作为起始位置的 s2 字符串继续比较。
当原始问题中 i 和 j 指向位置字符不相同时，存在三种选择。至于子问题如何求解，这个归功于递归思想。递归最大的好处就是只需要确定基础函数的功能，然后确定子问题，则子问题的内部如何求解站在宏观角度可以不管。反之它可以一步一步继续缩小问题规模，直到有答案为止。
在这里，我们可以使用递归函数来解决问题。例如：
```c
int lcs(string s1, int i, string s2, int j) {
if (s1[i] != s2[j]) {
// 有三种选择
int sel_1 = lcs(s1, i, s2, j + 1);
int sel_2 = lcs(s1, i + 1, s2, j);
int sel_3 = lcs(s1, i + 1, s2, j + 1);
return max(sel_1, sel_2, sel_3);
} else {
// 只有一个选择
return lcs(s1, i + 1, s2, j + 1) + 1;
}
}
```
在这里，我们使用递归思想来解决问题。当 i 和 j 指向位置字符相同时，必然在当前子问题中找到了一个公共字符，则最终结果就是后续子问题的结果基础上加 1，即为最长公共子序列为原来的值加 1。
递归边界。当 i==s1.size() 或 j==s2.size() 时，说明已经扫描到了子符串的最后。无论哪一个指针先到达字符串的末尾，则都不再存在任何公共子序列。
使用递归思想可以解决最长公共子序列的问题。这种思想可以帮助我们解决许多实际问题，使我们的代码更加简洁、高效。
