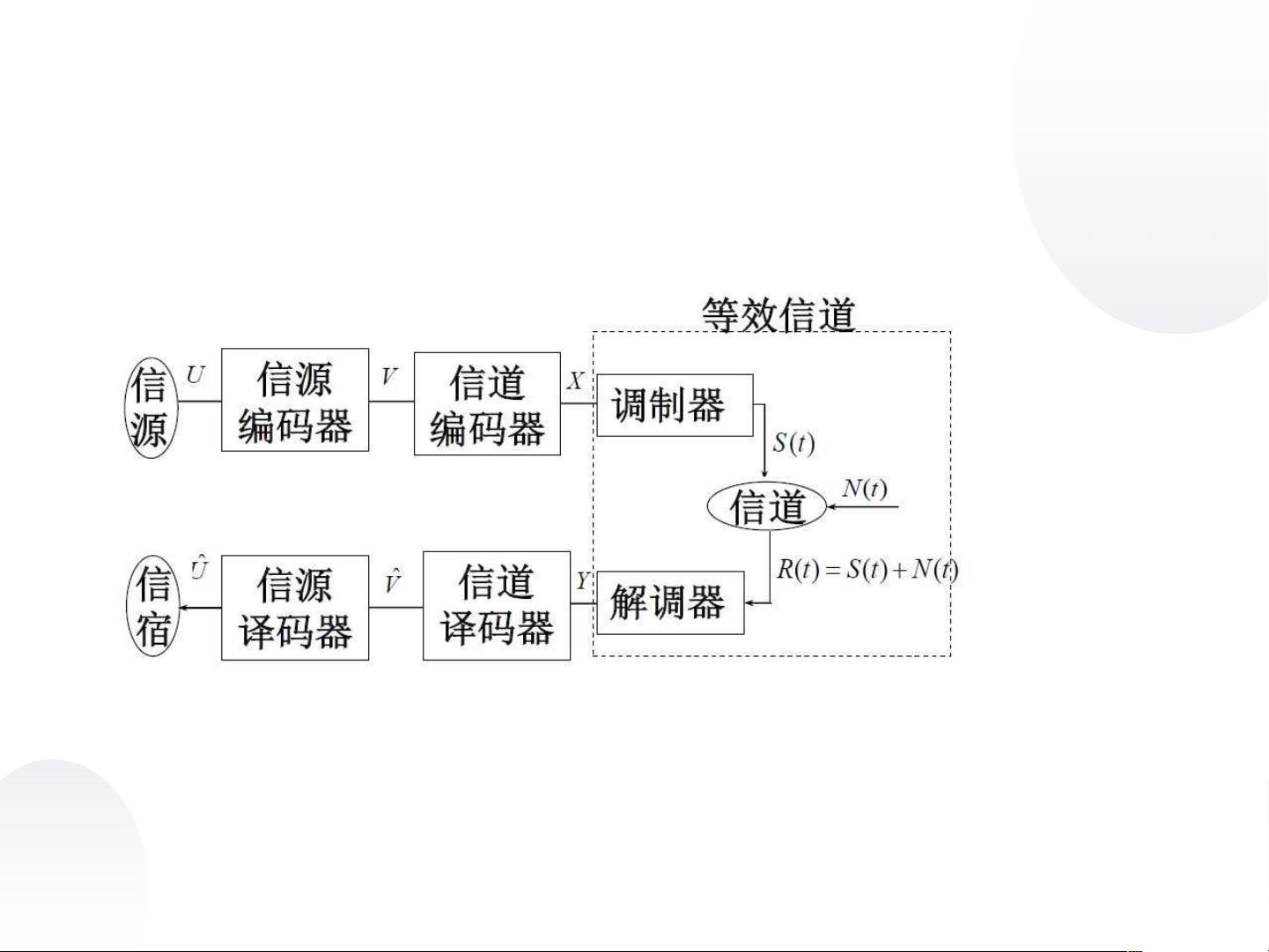
线性分组码是编码理论中的一个重要概念,它主要用于提高信息传输的可靠性。在通信系统中,信息源编码主要是为了提高传输效率,而信道编码则着重于增强系统的抗干扰能力,确保信息在有噪声的信道中传输时能够被准确接收。线性分组码是一种特殊的纠错码,它的特点是冗余位只与当前时刻输入的k位信息元有关,且这些冗余位是信息元的线性组合。
信道纠错编码的基本结构遵循香农第二定理,即在信息传输速率小于信道容量的情况下,存在编码和译码方法使得错误率可趋近于零。线性分组码通常用(n,k)来表示,其中n是码长,k是信息位数,r=n-k为冗余位数。这种码的纠错能力取决于冗余位的数量,冗余位越多,纠错能力越强,但同时会降低传输效率。
纠错码根据功能和结构可分为检错码、纠错码、纠删码、分组码和卷积码等。检错码只能检测错误,不能纠正;纠错码既能检测又能纠正错误;纠删码在超过纠正范围时会删除无法纠正的信息。分组码中,冗余位仅依赖当前的信息位,而卷积码的冗余位还与之前的信息位有关。线性码的冗余位是信息位的线性组合,而非线性码则不然。
循环码是线性分组码的一个特例,它的码字经过循环移位后仍然是码字,这为简化编码和译码提供了便利。码元可以是二元的,也可以是多元的,二元码所有码元取自二元域,多元码则取自多元域。
选择一个好的纠错码要考虑其纠错能力、编码和译码效率以及传输速率。纠错码的纠错能力通常指其能纠正的错误位数。快速有效的编码和译码算法是必要的,同时码的冗余开销要尽可能小,以最大化信息传输速率。
分组码的集合大小由信息字的长度和码字的元素域大小决定。例如,一个(6,3)二元分组码,信息字长度为3,码字长度为6,码集合大小为2^3=8。通过建立生成矩阵和校验矩阵,可以明确信息位与码位之间的关系,从而进行编码和译码。错误图样用于描述传输错误的位置,通过比较接收序列和码字,可以找出错误并进行纠正。
在实际应用中,接收到的码字可能包含错误,此时需要判断其是否为非法码字,如果是非法码字,通过译码算法确定错误位置和值,进而修复错误。这种方法是基于矩阵运算和特定的译码算法,如汉明码、BCH码或卷积码的Viterbi算法等。
线性分组码是提高通信可靠性的重要工具,通过合理设计和运用,可以在保证传输效率的同时,有效地检测和纠正传输过程中的错误。