在微积分的学习过程中,我们经常会遇到需要计算沿着特定路径上的物理量累加情况,比如求解变力沿曲线路径做功的问题。这就需要我们用到一个强大的数学工具——对坐标的曲线积分。通过对坐标的曲线积分,我们能够解决许多实际问题,如物理中的力的功、工程中的路径积分等。为了更好地理解这一概念,我们可以通过PPT课件的形式来深入探讨对坐标的曲线积分的定义、性质、计算方法以及它在实际问题中的应用。
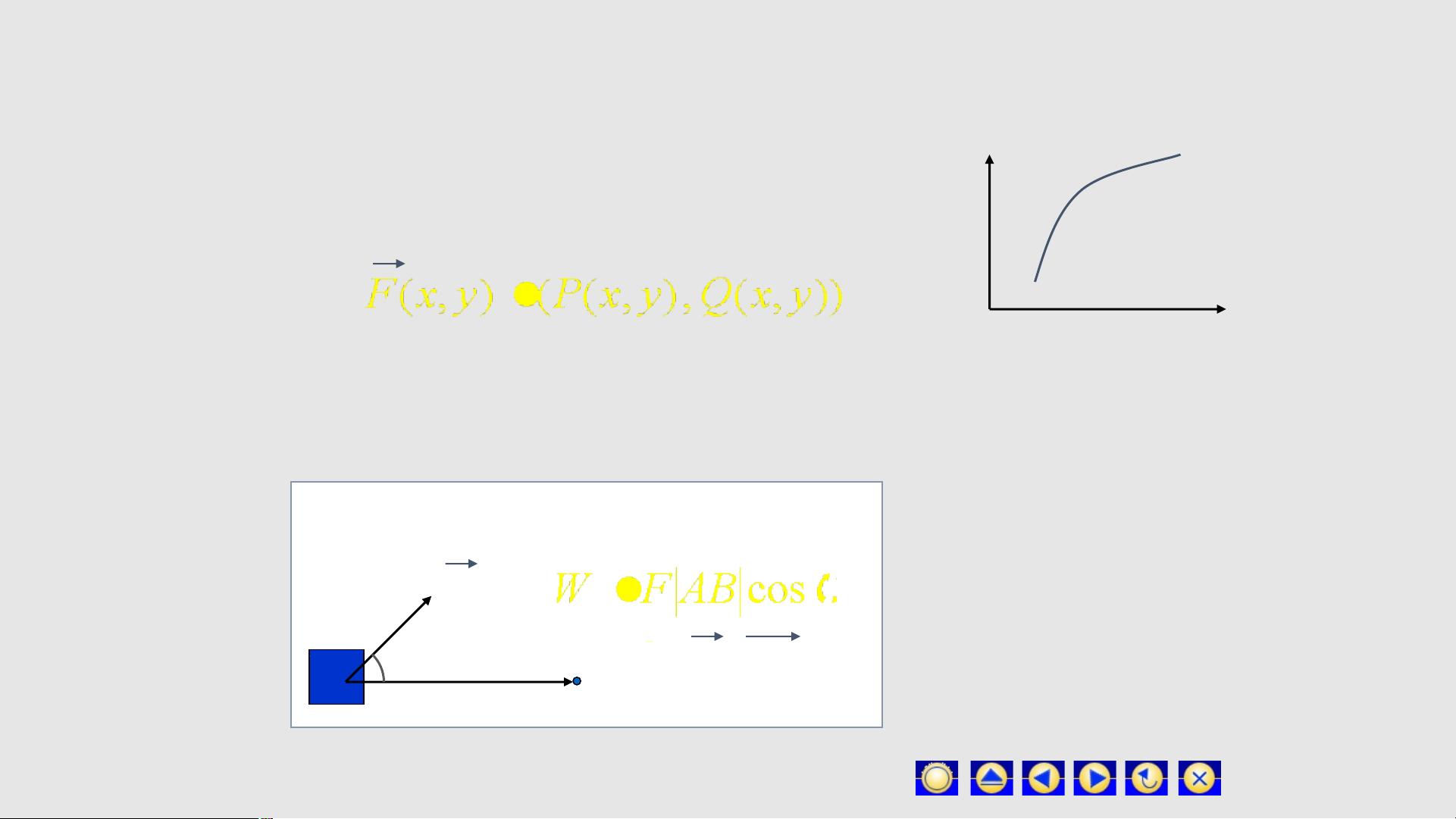
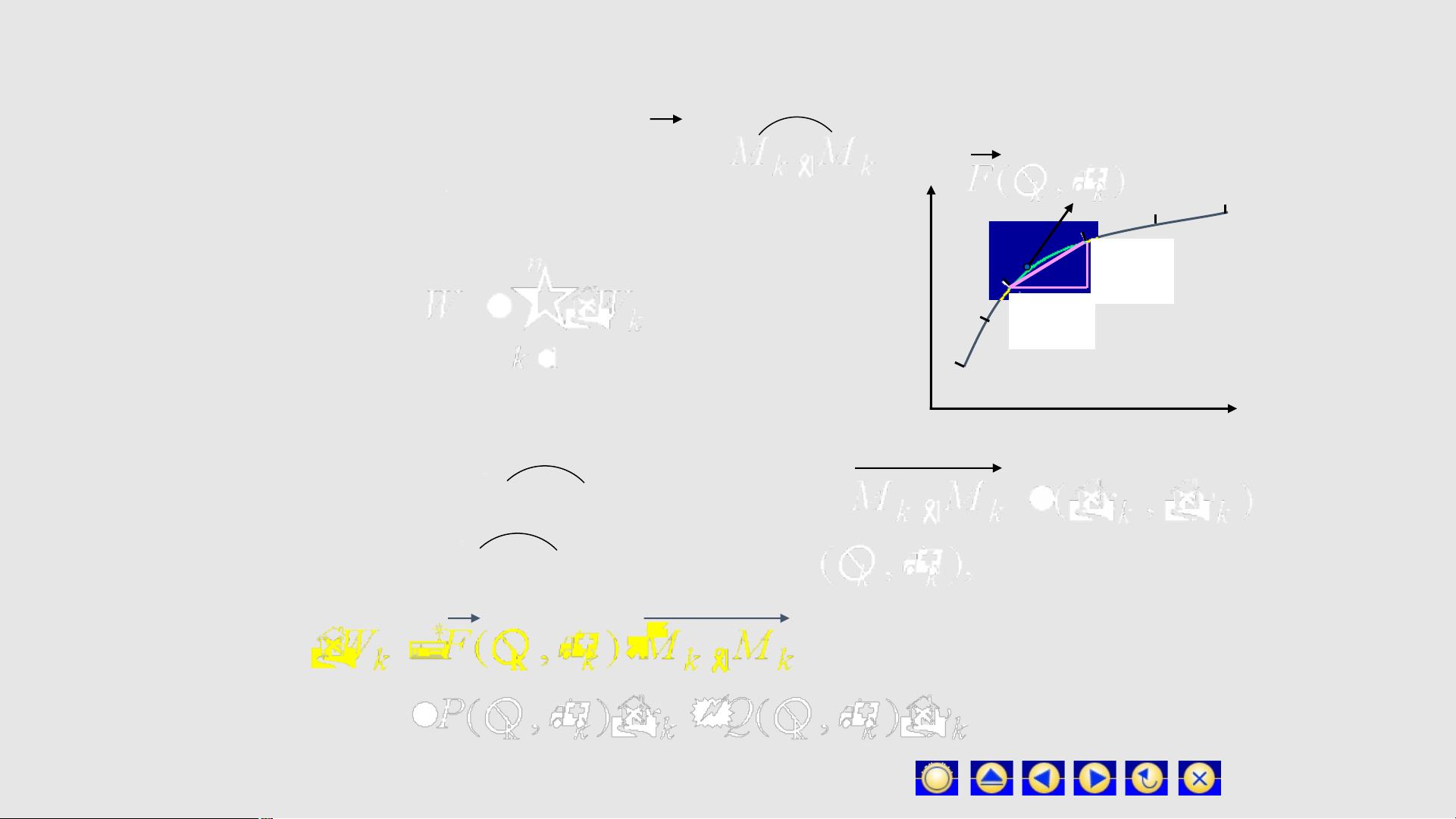
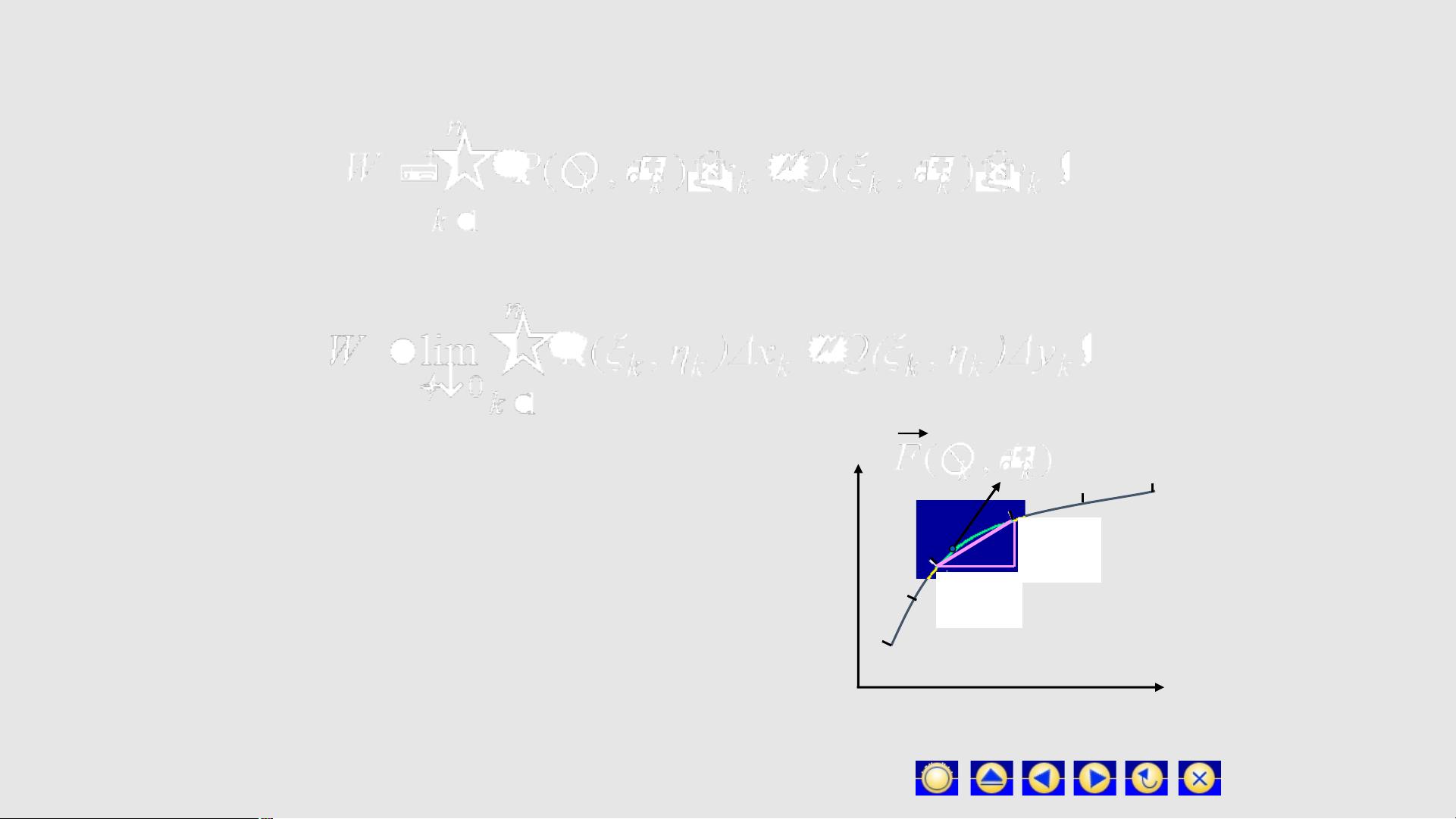
我们从一个实际问题入手,即变力沿曲线做功的计算。想象一个质点在空间中受到变力的作用,沿一条曲线移动,求变力在整个过程中的总功。为了解决这个问题,我们可以采用四步方法:将曲线分割成许多小段,这一步我们称之为“大化小”;用这些小段近似表示曲线,这就是“常代变”;然后,计算每个小段上的功并求和,称为“近似和”;当小段长度趋于零时,求和的极限就是总功,这一步称为“取极限”。这个极限就是我们所说的对坐标的曲线积分的定义。
在定义中,对坐标的曲线积分是指对任意曲线分割和局部弧段上的点,函数的极限存在时,这个极限被称为对坐标的曲线积分。若积分曲线在xy平面上,我们可以分别对x和y进行积分,记作或。对于空间曲线,积分形式类似。从这里可以看出,对坐标的曲线积分不仅是微积分中的重要概念,还是解决实际物理问题的有力工具。
PPT课件中进一步列出了对坐标的曲线积分的一些性质。例如,积分可以沿着曲线的任意分割进行,只要方向保持一致;积分值不会因曲线的反向而改变,这表明积分对方向敏感。此外,定积分是第二类曲线积分的特例,当积分曲线为直线时,此时的对坐标的曲线积分就退化为普通的定积分。
在具体计算对坐标的曲线积分时,我们可以利用曲线的参数方程。如果曲线L的参数方程是已知的,我们就可以将函数表达为关于参数的函数,然后进行积分。PPT中给出了一些具体的例子,如沿抛物线的积分,沿圆周的积分,以及计算力场对质点做功的情况。这些例子直观地展示了如何使用参数方程来简化对坐标的曲线积分的计算过程。
PPT讨论了两类曲线积分之间的关系,即第一类曲线积分(对弧长的积分)和第二类曲线积分(对坐标的积分)。它们之间可以通过曲线的切向量方向余弦建立联系。例如,可以将对坐标的积分转换为对弧长的积分,这对于某些问题的求解特别有用。这种转换为我们提供了一个新的角度去理解和处理复杂的曲线积分问题。
总体来说,对坐标的曲线积分是微积分中一个非常重要的概念。它不仅在理论上有其独特的性质和计算技巧,而且在物理学、工程学等领域的实际问题中也发挥着重要作用。通过PPT课件这种直观的教学形式,我们可以更深刻地理解对坐标的曲线积分的内涵,掌握其计算方法,并能够将其应用到更广泛的领域中去。